神经网络基础篇：详解导数（Derivatives）

导数

一个函数\(f(a)=3a\)，它是一条直线。下面来简单理解下导数。让 看看函数中几个点，假定\(a=2\)，那么\(f(a)\)是\(a\)的3倍等于6，也就是说如果\(a=2\)，那么函数\(f(a)=6\)。假定稍微改变一点点\(a\)的值，只增加一点，变为2.001，这时\(a\)将向右做微小的移动。0.001的差别实在是太小了，不能在图中显示出来， 把它右移一点，现在\(f(a)\)等于\(a\)的3倍是6.003，画在图里，比例不太符合。请看绿色高亮部分的这个小三角形，如果向右移动0.001，那么\(f(a)\)增加0.003，\(f(a)\)的值增加3倍于右移的\(a\)，因此 说函数\(f(a)\)在\(a=2\)，.是这个导数的斜率，或者说，当\(a=2\)时，斜率是3。导数这个概念意味着斜率，导数听起来是一个很可怕、很令人惊恐的词，但是斜率以一种很友好的方式来描述导数这个概念。所以提到导数， 把它当作函数的斜率就好了。更正式的斜率定义为在上图这个绿色的小三角形中，高除以宽。即斜率等于0.003除以0.001，等于3。或者说导数等于3，这表示当 将\(a\)右移0.001，\(f(a)\)的值增加3倍水平方向的量。

现在让从不同的角度理解这个函数。
假设\(a=5\) ，此时\(f(a)=3a=15\)。
把\(a\)右移一个很小的幅度，增加到5.001，\(f(a)=15.003\)。
即在\(a=5\) 时，斜率是3，这就是表示，当微小改变变量\(a\)的值，\(\frac{df(a)}{da}=3\) 。一个等价的导数表达式可以这样写\(\frac{d}{da}f(a)\)，不管 是否将\(f(a)\)放在上面或者放在右边都没有关系。
在这个博客中， 讲解导数讨论的情况是 将\(a\)偏移0.001，如果 想知道导数的数学定义，导数是 右移很小的\(a\)值（不是0.001，而是一个非常非常小的值）。通常导数的定义是 右移\(a\)(可度量的值)一个无限小的值，\(f(a)\)增加3倍（增加了一个非常非常小的值）。也就是这个三角形右边的高度。

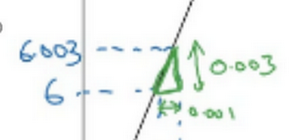
那就是导数的正式定义。但是为了直观的认识， 将探讨右移\(a=0.001\) 这个值，即使0.001并不是无穷小的可测数据。导数的一个特性是：这个函数任何地方的斜率总是等于3，不管\(a=2\)或 \(a=5\)，这个函数的斜率总等于3，也就是说不管\(a\)的值如何变化，如果 增加0.001，\(f(a)\)的值就增加3倍。这个函数在所有地方的斜率都相等。一种证明方式是无论 将小三角形画在哪里，它的高除以宽总是3。

希望带给你一种感觉：什么是斜率？什么是导函数？对于一条直线，在例子中函数的斜率，在任何地方都是3。

2.6 更多的导数例子（More Derivative Examples）

在这个博客中 将给出一个更加复杂的例子，在这个例子中，函数在不同点处的斜率是不一样的，先来举个例子:

在这里画一个函数，\(f(a)={{\text{a}}^{\text{2}}}\)，如果\(a=\text{2}\) 的话，那么\(f(a)=4\)。让 稍稍往右推进一点点，现在\(a=\text{2}.\text{001}\) ，则\(f(a)\approx 4.004\) (如果 用计算器算的话，这个准确的值应该为4.004。0.001 只是为了简便起见，省略了后面的部分)，如果 在这儿画，一个小三角形， 就会发现，如果把\(a\)往右移动0.001，那么\(f(a)\)将增大四倍，即增大0.004。在微积分中 把这个三角形斜边的斜率，称为\(f(a)\)在点\(a=\text{2}\) 处的导数(即为4)，或者写成微积分的形式，当\(a=\text{2}\) 的时候， \(\frac{d}{da}f(a)=4\) 由此可知，函数\(f(a)={{a}^{{2}}}\)，在\(a\)取不同值的时候，它的斜率是不同的，这和上个博客中的例子是不同的。

这里有种直观的方法可以解释，为什么一个点的斜率，在不同位置会不同如果 在曲线上，的不同位置画一些小小的三角形 就会发现，三角形高和宽的比值，在曲线上不同的地方，它们是不同的。所以当\(a=2\) 时，斜率为4；而当\(a=5\)时，斜率为10 。如果 翻看微积分的课本，课本会告诉 ，函数\(f(a)={{a}^{{2}}}\)的斜率（即导数）为\(2a\)。这意味着任意给定一点\(a\)，如果 稍微将\(a\)，增大0.001，那么 会看到\(f(a)\)将增大\(2a\)，即增大的值为点在\(a\)处斜率或导数，乘以 向右移动的距离。

注意：导数增大的值，不是刚好等于导数公式算出来的值，而只是根据导数算出来的一个估计值。

为了总结这篇博客的知识， 再来看看几个例子：

假设\(f(a)={{a}^{\text{3}}}\) 如果 翻看导数公式表， 会发现这个函数的导数，等于\(3{{a}^{2}}\)。所以这是什么意思呢，同样地举一个例子： 再次令\(a=2\)，所以\({{a}^{3}}=8\) ，如果 又将\(a\)增大一点点， 会发现\(f(a)\approx 8.012\)， 可以自己检查一遍，如果 取8.012， 会发现\({{2.001}^{3}}\) ，和8.012很接近，事实上当\(a=2\)时，导数值为\(3×{{2}^{2}}\)，即\(3×4=12\)。所以导数公式，表明如果 将\(a\)向右移动0.001时，\(f(a)\) 将会向右移动12倍，即0.012。

来看最后一个例子，假设\(f(a)={{\log }_{e}}a\)，有些可能会写作\(\ln a\)，函数\(\log a\) 的斜率应该为\(\frac{1}{a}\)，所以 可以解释如下：如果\(a\)取任何值，比如又取\(a=2\)，然后又把\(a\)向右边移动0.001 那么\(f(a)\)将增大\(\frac{\text{1}}{a}\times \text{0}\text{.001}\)，如果 借助计算器的话， 会发现当\(a=2\)时\(f(a)\approx \text{0}\text{.69315}\) ；而\(a=2.001\)时，\(f(a)\approx \text{0}\text{.69365}\)。所以\(f(a)\)增大了0.0005，如果 查看导数公式，当\(a=2\)的时候，导数值\(\frac{d}{da}f(a)=\frac{\text{1}}{\text{2}}\)。这表明如果 把 增大0.001，\(f(a)\)将只会增大0.001的二分之一，即0.0005。如果 画个小三角形 就会发现，如果\(x\) 轴增加了0.001，那么\(y\) 轴上的函数\(\log a\)，将增大0.001的一半 即0.0005。所以 \(\frac{1}{a}\) ，当\(a=2\)时这里是 ，就是当\(a=2\)时这条线的斜率。这些就是有关，导数的一些知识。

在这个博客中，只需要记住两点：

• 第一点，导数就是斜率，而函数的斜率，在不同的点是不同的。在第一个例子中\(f(a)=\text{3}a\) ，这是一条直线，在任何点它的斜率都是相同的，均为3。但是对于函数\(f(a)={{\text{a}}^{\text{2}}}\) ，或者\(f(a)=\log a\)，它们的斜率是变化的，所以它们的导数或者斜率，在曲线上不同的点处是不同的。

• 第二点，如果想知道一个函数的导数， 可参考微积分课本或者维基百科，然后 应该就能找到这些函数的导数公式。