神经网络基础篇：逻辑回归

逻辑回归(Logistic Regression)

对于二元分类问题来讲，给定一个输入特征向量$X$，它可能对应一张图片，想识别这张图片识别看它是否是一只猫或者不是一只猫的图片，想要一个算法能够输出预测，只能称之为$\hat{y}$，也就是对实际值 $y$ 的估计。更正式地来说，想让 $\hat{y}$ 表示 $y$ 等于1的一种可能性或者是机会，前提条件是给定了输入特征$X$。换句话来说，如果$X$是上篇博客的图片，想让 $\hat{y}$ 来告诉这是一只猫的图片的机率有多大。在之前博客中所说的，$X$是一个$n_x$维的向量（相当于有$n_x$个特征的特征向量）。用$w$来表示逻辑回归的参数，这也是一个$n_x$维向量（因为$w$实际上是特征权重，维度与特征向量相同），参数里面还有$b$，这是一个实数（表示偏差）。所以给出输入$x$以及参数$w$和$b$之后，怎样产生输出预测值$\hat{y}$，一件可以尝试却不可行的事是让$\hat{y}={{w}^{T}}x+b$。

这时候得到的是一个关于输入$x$的线性函数，实际上这是在做线性回归时所用到的，但是这对于二元分类问题来讲不是一个非常好的算法，因为想让$\hat{y}$表示实际值$y$等于1的机率的话，$\hat{y}$ 应该在0到1之间。这是一个需要解决的问题，因为${{w}^{T}}x+b$可能比1要大得多，或者甚至为一个负值。对于想要的在0和1之间的概率来说它是没有意义的，因此在逻辑回归中，输出应该是$\hat{y}$等于由上面得到的线性函数式子作为自变量的sigmoid函数中，公式如上图最下面所示，将线性函数转换为非线性函数。

下图是sigmoid函数的图像，如果我把水平轴作为$z$轴，那么关于$z$的sigmoid函数是这样的，它是平滑地从0走向1，让我在这里标记纵轴，这是0，曲线与纵轴相交的截距是0.5，这就是关于$z$的sigmoid函数的图像。通常都使用$z$来表示${{w}^{T}}x+b$的值。

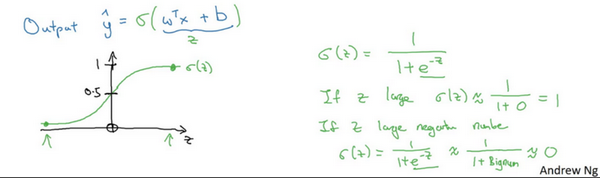
关于sigmoid函数的公式是这样的，$\sigma \left( z \right)=\frac{1}{1+{{e}^{-z}}}$,在这里$z$是一个实数，这里要说明一些要注意的事情，如果$z$非常大那么${{e}^{-z}}$将会接近于0，关于$z$的sigmoid函数将会近似等于1除以1加上某个非常接近于0的项，因为$e$ 的指数如果是个绝对值很大的负数的话，这项将会接近于0，所以如果$z$很大的话那么关于$z$的sigmoid函数会非常接近1。相反地，如果$z$非常小或者说是一个绝对值很大的负数，那么关于${{e}^{-z}}$这项会变成一个很大的数，可以认为这是1除以1加上一个非常非常大的数，所以这个就接近于0。实际上看到当$z$变成一个绝对值很大的负数，关于$z$的sigmoid函数就会非常接近于0，因此当实现逻辑回归时，的工作就是去让机器学习参数$w$以及$b$这样才使得$\hat{y}$成为对$y=1$这一情况的概率的一个很好的估计。

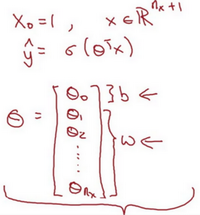
在继续进行下一步之前，介绍一种符号惯例，可以让参数$w$和参数$b$分开。在符号上要注意的一点是当对神经网络进行编程时经常会让参数$w$和参数$b$分开，在这里参数$b$对应的是一种偏置。在机器学习里也有处理这个问题时的其他符号表示。比如在某些例子里，定义一个额外的特征称之为${{x}_{0}}$，并且使它等于1，那么现在$X$就是一个$n_x$加1维的变量，然后定义$\hat{y}=\sigma \left( {{\theta }^{T}}x \right)$的sigmoid函数。在这个备选的符号惯例里，有一个参数向量${{\theta }_{0}},{{\theta }_{1}},{{\theta }_{2}},...,{{\theta }_{{{n}_{x}}}}$，这样${{\theta }_{0}}$就充当了$b$，这是一个实数，而剩下的${{\theta }_{1}}$ 直到${{\theta }_{{{n}_{x}}}}$充当了$w$，结果就是当实现的神经网络时，有一个比较简单的方法是保持$b$和$w$分开。但是在我写的博客中不会使用任何这类符号惯例，所以不用担心。
现在已经知道逻辑回归模型是什么样子了，下一步要做的是训练参数$w$和参数$b$，需要定义一个代价函数。

逻辑回归的代价函数（Logistic Regression Cost Function）

为什么需要代价函数：

为了训练逻辑回归模型的参数参数$w$和参数$b$，需要一个代价函数，通过训练代价函数来得到参数$w$和参数$b$。先看一下逻辑回归的输出函数：

为了让模型通过学习调整参数，需要给予一个$m$样本的训练集，这会让在训练集上找到参数$w$和参数$b$,，来得到的输出。

对训练集的预测值，将它写成$\hat{y}$，更希望它会接近于训练集中的$y$值，为了对上面的公式更详细的介绍，需要说明上面的定义是对一个训练样本来说的，这种形式也使用于每个训练样本，使用这些带有圆括号的上标来区分索引和样本，训练样本$i$所对应的预测值是${{y}^{(i)}}$,是用训练样本的${{w}^{T}}{{x}^{(i)}}+b$然后通过sigmoid函数来得到，也可以把$z$定义为${{z}^{(i)}}={{w}^{T}}{{x}^{(i)}}+b$,将使用这个符号$(i)$注解，上标$(i)$来指明数据表示$x$或者$y$或者$z$或者其他数据的第$i$个训练样本，这就是上标$(i)$的含义。

损失函数：

损失函数又叫做误差函数，用来衡量算法的运行情况，Loss function:$L\left( \hat{y},y \right)$.

通过这个$L$称为的损失函数，来衡量预测输出值和实际值有多接近。一般用预测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中不这么做，因为当在学习逻辑回归参数的时候，会发现的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值，虽然平方差是一个不错的损失函数，但是在逻辑回归模型中会定义另外一个损失函数。

在逻辑回归中用到的损失函数是：$L\left( \hat{y},y \right)=-y\log(\hat{y})-(1-y)\log (1-\hat{y})$

为什么要用这个函数作为逻辑损失函数？当使用平方误差作为损失函数的时候，会想要让这个误差尽可能地小，对于这个逻辑回归损失函数，也想让它尽可能地小，为了更好地理解这个损失函数怎么起作用，举两个例子：

当$y=1$时损失函数$L=-\log (\hat{y})$，如果想要损失函数$L$尽可能得小，那么$\hat{y}$就要尽可能大，因为sigmoid函数取值$[0,1]$，所以$\hat{y}$会无限接近于1。

当$y=0$时损失函数$L=-\log (1-\hat{y})$，如果想要损失函数$L$尽可能得小，那么$\hat{y}$就要尽可能小，因为sigmoid函数取值$[0,1]$，所以$\hat{y}$会无限接近于0。

有很多的函数效果和现在这个类似，就是如果$y$等于1，就尽可能让$\hat{y}$变大，如果$y$等于0，就尽可能让 $\hat{y}$ 变小。
损失函数是在单个训练样本中定义的，它衡量的是算法在单个训练样本中表现如何，为了衡量算法在全部训练样本上的表现如何，需要定义一个算法的代价函数，算法的代价函数是对$m$个样本的损失函数求和然后除以$m$:
$J\left( w,b \right)=\frac{1}{m}\sum\limits_{i=1}^{m}{L\left( {{{\hat{y}}}^{(i)}},{{y}^{(i)}} \right)}=\frac{1}{m}\sum\limits_{i=1}^{m}{\left( -{{y}^{(i)}}\log {{{\hat{y}}}^{(i)}}-(1-{{y}^{(i)}})\log (1-{{{\hat{y}}}^{(i)}}) \right)}$
损失函数只适用于像这样的单个训练样本，而代价函数是参数的总代价，所以在训练逻辑回归模型时候，需要找到合适的$w$和$b$，来让代价函数 $J$ 的总代价降到最低。
根据对逻辑回归算法的推导及对单个样本的损失函数的推导和针对算法所选用参数的总代价函数的推导，结果表明逻辑回归可以看做是一个非常小的神经网络。