假几何真逆序数 NB HDU3465

题意：

有n条直线，问他们两两在横坐标开区间（L，R）之间相交的个数

 

n=50000，暴力肯定就不用想了，如果在纸上画一画可以发现如果两条直线在（L，R）内相交，那么他们与x= L和x=R的交点序数是相反的

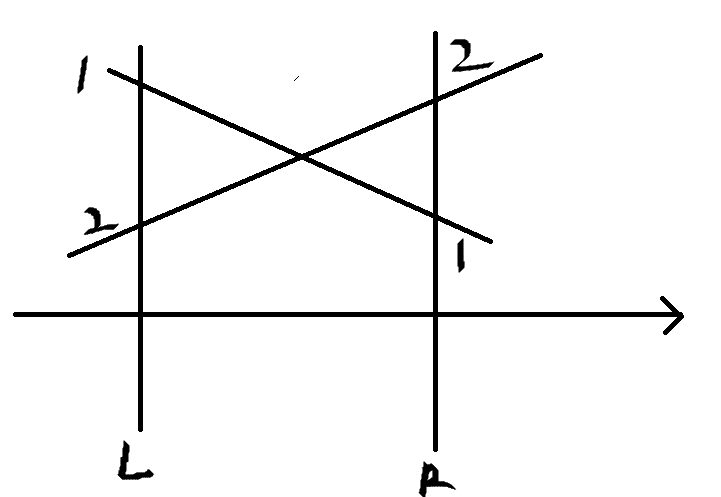
所以我们只需要算与x=L的交点，然后根据这些点排序编个号，在与R相交，根据新的交点排个逆序，根据编号求逆序数即可。

需要注意的一点:两种特殊情况如果不与L，R相交，那么如果再这个区间内，必定所有直线都会与之相交，记录下数量。

另一种情况就是，如果两个直线的交点正巧在x=L和x=R时， 这种情况是不能记录在内的，那么在之前排序的时候与L相交的交点按升序排列

如果交点坐标相同按R交点坐标升序，再根据R的坐标排降序的时候，如果R坐标相同，根据L的坐标排降序，就可以避免这种情况计算在内了。

求逆序数的时候是不会计算在里面的。

 

求逆序数树状数组即可。

  1 #include <stdio.h>
  2 #include <string.h>
  3 #include <iostream>
  4 #include <queue>
  5 #include <vector>
  6 #include <algorithm>
  7 #include <stack>
  8 #include <set>
  9 #include <map>
 10 #include <cmath>
 11 #define pb push_back
 12 #define CLR(a) memset(a, 0, sizeof(a));
 13 #define MEM(a, b) memset(a, b, sizeof(a));
 14 #define fi first
 15 #define se second
 16 
 17 using namespace std;
 18 
 19 typedef long long ll;
 20 
 21 const int MAXN = 50007;
 22 const int MAXV = 207;
 23 const int MAXE = 207;
 24 const int INF = 0x3f3f3f3f;
 25  
 26 int n;
 27 
 28 struct Node
 29 {
 30     double a, b;
 31     int nu;
 32     Node () {}
 33     Node (double a, double b) : a(a), b(b) {}
 34 }node[MAXN];
 35 double L, R;
 36 
 37 bool cmpl(Node n1, Node n2)
 38 {
 39     if (n1.a == n2.a)
 40         return n1.b < n2.b;
 41     else return n1.a < n2.a;
 42 }
 43 bool cmpr(Node n1, Node n2)
 44 {
 45     if (n1.b == n2.b)
 46         return n1.a > n2.a;
 47     else return n1.b > n2.b;
 48 }
 49 int cnt = 0;
 50 int c[MAXN << 1];
 51 int lowbit(int x)
 52 {
 53     return x&(-x);
 54 }
 55 void modify(int x, int data)
 56 {
 57     for (int i = x; i < MAXN; i+= lowbit(i))
 58         c[i] += data;
 59 }
 60 int getsum(int x)
 61 {
 62     int res = 0;
 63     for (int i = x; i > 0; i -= lowbit(i))
 64         res += c[i];
 65     return res;
 66 }
 67 
 68 int main()
 69 {
 70     while (~scanf("%d", &n))
 71     {
 72         CLR(node);
 73         CLR(c);
 74         scanf("%lf%lf", &L, &R);
 75         cnt = 0;
 76         int vrtcl = 0;
 77         for (int i = 0; i < n; i++)
 78         {
 79             double x1, y1, x2, y2;
 80             scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
 81             if (x1 == x2)
 82             {
 83                 if (x1 > L && x1 < R) vrtcl++;
 84                 continue;
 85             }
 86             double k = (y2-y1)/(x2-x1);
 87             double b = y2 - k*x2;
 88             double l = k*L+b, r = k*R+b;
 89             node[cnt++] = Node(l, r);
 90         }
 91         sort(node, node+cnt, cmpl);
 92         for (int i = 0; i < cnt; i++) node[i].nu = i+1;
 93         sort(node, node+cnt, cmpr);
 94         //for (int i = 0; i < cnt; i++) cout << node[i].nu << endl;
 95         int ans = 0;
 96         for (int i = 0; i < cnt; i++)
 97         {
 98             ans += getsum(node[i].nu);
 99             modify(node[i].nu, 1);
100         }
101         ans += cnt*vrtcl;
102         cout << ans << endl;
103     }
104     return 0;
105 }

 

posted @ 2017-09-30 16:45  Lorazepam  阅读(228)  评论(0)  编辑  收藏  举报