斜率优化dp学习
用了一堂半的课才彻底搞懂。其他神犇写的博客或多或少有点小bug,所以orzzz不才斗胆重新写一个。
里面大量穿用其他神犇的原话,就不逐一标明出处了。
引用资料 Accept的博客 MathonL的博客

首先是最经典的题的题面。
HDU 3507,很适合的一个入门题。
大概题意就是要输出$N$个数字$a[N]$,输出的时候可以连续连续的输出,每连续输出一串,它的费用是 “这串数字和的平方加上一个常数$M$”。
我们设$dp[i]$表示输出到$i$的时候最少的花费,$S[i]$表示从$a[1]$到$a[i-1]$的数字和。注意这里为了方便起见前缀和与一般的有区别。
则有:$dp[i]=min \left\{ dp[j]+(S[i+1]-S[j])^2+M \right\} (j<i)$
复杂度显然是$O(n^2)$的。对于$500000$的$n$显然过不了。那么我们想,能否在$O(1)$时间内找到所有转移里最优的那个呢?
我们假设在求解$dp[i]$时,存在$j,k(j>k)$使得从$j$转移比从$k$转移更优,那么需要满足条件:
$dp[j]+(S[i+1]-S[j])^2+M<dp[k]+(S[i+1]-S[k])^2+M$
展开上式
$dp[j]+S[i+1]^2-2S[i+1]S[j]+S[j]^2+M<dp[k]+S[i+1]^2-2S[i+1]S[k]+S[k]^2+M$
移项并消去再合并同类项得
$dp[j]-dp[k]+S[j]^2-S[k]^2<2S[i+1](S[j]-S[k])$
把$S[j]-S[k]$除过去,得到
$\frac{dp[j]-dp[k]+S[j]^2-S[k]^2}{S[j]-S[k]}<2S[i+1]$
我们设$f[x]=dp[x]+S[x]^2$,就化成了
$\frac{f[j]-f[k]}{S[j]-S[k]}<2S[i+1]$
即当$(j>k)$时,若$\frac{f[j]-f[k]}{S[j]-S[k]}<2S[i+1]$,则$j$对更新$dp[i]$比$k$更新$dp[i]$优。
休息一下qwq。这个东西好像斜率。
当一个数的$dp$值求完了,它的$f$值也跟着确定,我们就可以在空间中绘制出点$(S[i],f[i])$。这个点代表已经求出$dp$值的一个点。
当我们要求解$dp[t]$时,如果可用的集合里存在这样三个点,位置关系如图所示:
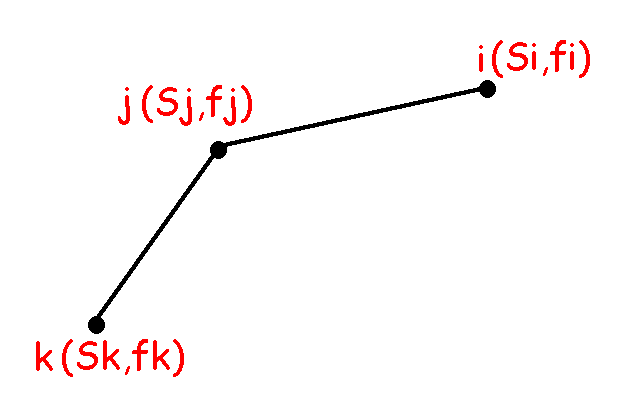
那么显然
$\frac{f[j]-f[k]}{S[j]-S[k]}>\frac{f[i]-f[j]}{S[i]-S[j]}$
这时候他们和$2S[t+1]$的关系有3种:
·$\frac{f[j]-f[k]}{S[j]-S[k]}>\frac{f[i]-f[j]}{S[i]-S[j]}>2S[t+1]$
那么$j$比$i$优,$k$比$j$优。
·$\frac{f[j]-f[k]}{S[j]-S[k]}>2S[t+1]>\frac{f[i]-f[j]}{S[i]-S[j]}$
那么$i$比$j$优,$k$比$j$优。
·$2S[t+1]>\frac{f[j]-f[k]}{S[j]-S[k]}>\frac{f[i]-f[j]}{S[i]-S[j]}$
那么$i$比$j$优,$j$比$k$优。
综上,不管什么样的$S[t+1]$,从$j$转移都不会是最佳方案。那么用一个数据结构维护一个凸包(下凸),每加入一个点就删去一些点,使其维持凸包的形态。最优转移一定在这个凸包中。
但还是不能$O(1)$对吧。在凸包里,谁又是最最优呢?
首先一定数据结构里的凸包一定会是这样的:
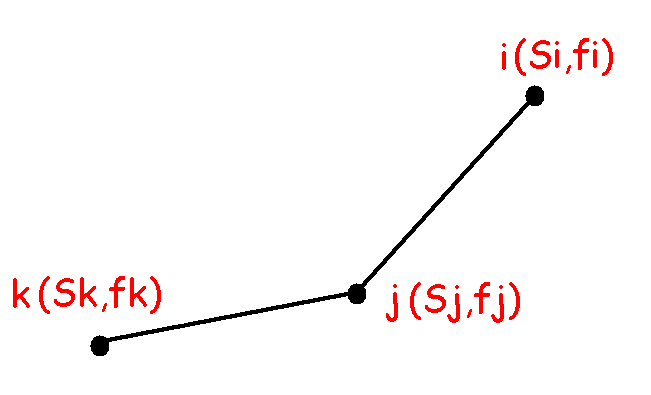
假设$\overrightarrow{ji}$的斜率$>2S[t+1]$且$\overrightarrow{kj}$的斜率$<2S[t+1]$从图形特点我们可以发现$j$点比所有比$k$小的点都优,比所有比$i$大的也优。所以对于我们二分查找斜率比$2S[t+1]$小的编号最大的点,就是最优的转移点。由于$S[i]$也满足单调性,我们还可以直接维护一个单调队列就能解决这个问题。
推广一下,如果不等式右侧不是像$S[i+1]$这样的单调函数,二分就好了。
所有小于等于的情况我都没提,想一想就知道了。重要的是思想啊对不对~
(我会说我一道斜率优化题都没做就写了这篇博客吗
upd1:
光会思想没有用啊,,,边界条件的处理很蛋疼的说
还是要自己写几遍qwq
upd2:
更正了一个bug,由@Duan2baka发现。不好好女装居然来看我这篇菜鸡博客。
upd3:
dp式子都写错了。。。感谢@自为风月马前卒指正
upd4:
我这bug也够多了哈。。感谢@belief01指正
upd5:
如果影响大家曾经的阅读深表歉意~虽然不是老师,但是千万不要误人子弟啊。。


