[bzoj1925][Sdoi2010]地精部落

大佬们好神啊，考试都切掉了这题，，本来以为T3可做写完发现不对结果T2还崩了。qwq好闹心啊。。。

找到了一个不玄乎的题解至少转移我看懂了。。clj的都太神了我等蒟蒻不能理解qwq

转自 http://www.xuebuyuan.com/1776773.html

题意：求$1$到$n$个所有排列中有多少种满足高低交错。

思路：$f[n][k]$表示n个数，最后一个为$k$且最后两个递增，$g[n][k]$表示$n$个数最后一个数为$k$且最后两个递减。对于$f[n][k]$，若我们将每个数$x$换为$n+1-x$，则就成了$g[n][n+1-k]$，因此有：$f[n][k]=g[n][n+1-k]$。那么可得：

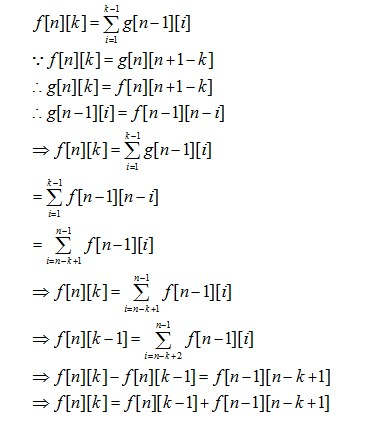
 由于对称性，我们计算出：

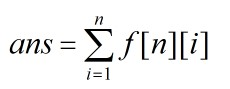
那么最后的答案就是$ans*2$。

---

 

 

#include<bits/stdc++.h>
typedef long long ll;
using namespace std;
const int N=10005;
ll f[2][N],ans;
int n,p;
int main(){
    cin>>n>>p;
    if(n==1) ans=1;
    if(n==2) ans=2;
    f[0][1]=0;f[0][2]=1;
    for(int i=3;i<=n;i++){
        int k=i&1;
        for(int j=1;j<=i;j++){
            f[k][j]=f[k^1][i-j+1]+f[k][j-1];
            f[k][j]%=p;
        }
    } 
    for(int i=1;i<=n;i++)
    ans=(ans+f[n&1][i])%p;
    cout<<(ans*2)%p;
}