Manacher算法详解
首先我们知道回文的定义:正反读都是一样的字符串叫做回文串。如:madam,lol,oppo,zz,甚至连单字符都可以被称为回文(串)。上面的例子可以看出,回文串可以分为两种:奇数回文和偶数回文。
如果我们想知道以一个字符串的所有子串中,最长的回文串是多长,怎么办呢?
首先想到用裸的枚举中心,然后扩展边界方法来求回文(比如对于hellomadams以d为中心,首先a=a,然后m=m,再然后o!=s找到以d为中心最长回文),我们就会发现第一个难题:偶数回文串并没有以字符为中心。那怎么扩展边界呢?
有一种特别巧妙的方法解决了这个问题。如下:
比如oppovivo这个串,我们在每两个字符之间加上一个特殊符号,通常用#来充当,这样变为了o#p#p#o#v#i#v#o。
那么oppo成为了以第二个‘#’为中心的回文,viv仍是以i为中心的回文。同时我们在首尾加上两个不同的特殊字符,通常就用‘@’,‘$'。这样连边界的判断都省了不是~到了首或尾,一定会因为字符不同结束扩展。
这部分的代码给一下。
void init(int n){
s[0]='@';
for(int i=1;i<=n;i++){
s[i*2-1]=str[i-1];
s[i*2]='#';
}
s[n*2]='$';
}
str是读进来的串,s是修改后的。
以上部分仅是铺垫manacher的精髓在于:充分利用已有条件,使复杂度降为O(n)。
以下图片均来自于博客http://blog.csdn.net/dyx404514/article/details/42061017
首先,我们要求什么:len数组,len[i]表示以s[i]为中心的最长回文串半径是多少。str转换为s后,所有回文长度一定是奇数。
我们还需要两个变量Po,mx。由于是递推求解,mx表示之前计算中最长回文子串的右端点的最大值,Po表示取得这个最大值的中点。在图中P就是上述mx。
i是接下来要求len值的点。
情况一:
设i关于Po的对称点是j,即j=2Po-i。
(1) i+len[j] < mx.
如图。
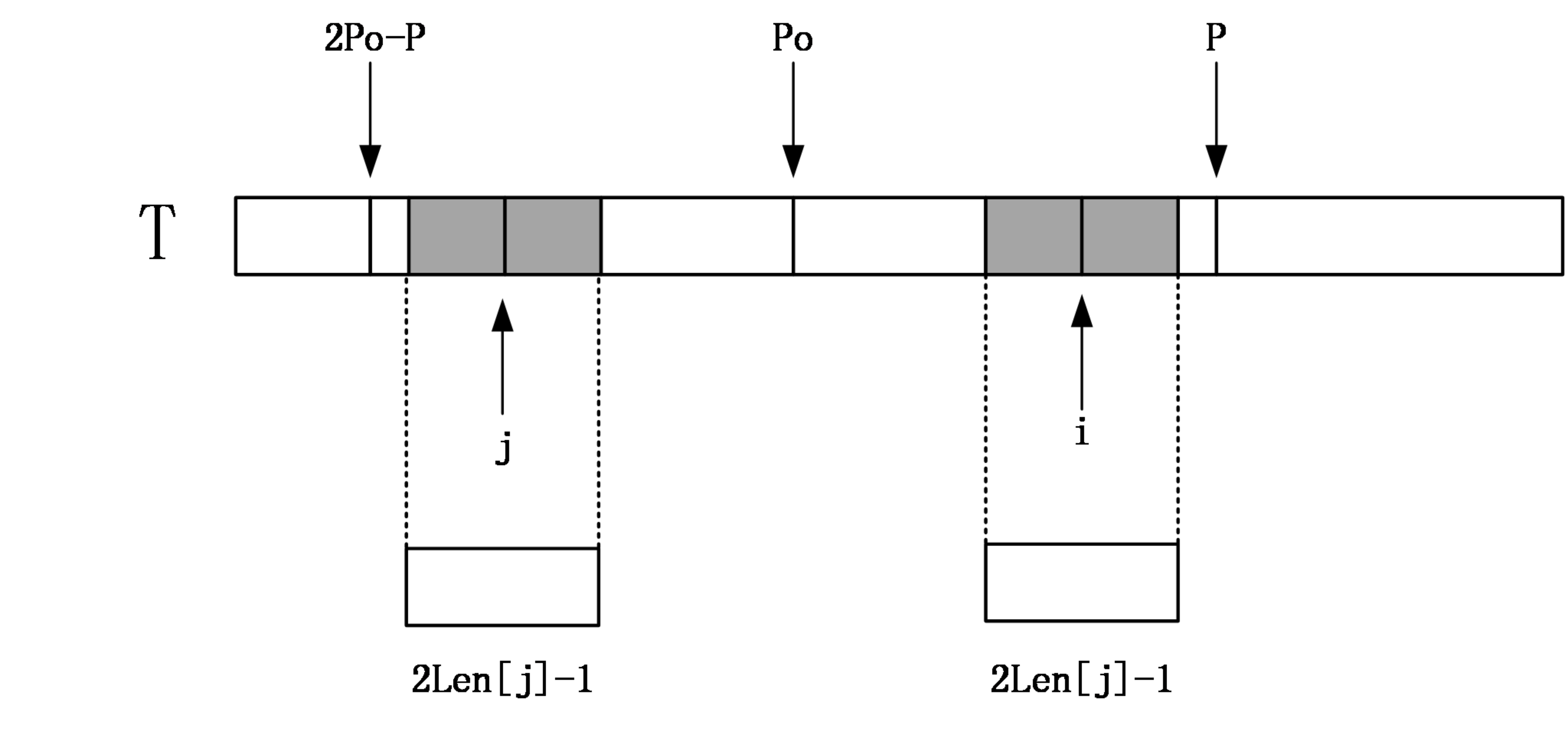
因为i是在当前端点最靠右的回文串之内,所以他一定有一个关于Po的对称点j。i、j位置上的字符一定是一样的。
不仅如此,以j为中心的最大回文串也一定等于以i为中心的最大回文串。len[j]已知,如果i的半径比len[j]大,哪怕是一个字符,根据他们关于Po对称且不在[2Po-mx,mx]范围外可知,len[j]就还能扩展,len[j]的求解就是矛盾的。
所以此时len[i]=len[j]即可。
(2) i+len[j] >= mx
如图。
与上一种情况同理。在[2Po-mx,mx]范围内的,以i,j为中心的部分是相等的(阴影部分)。这时i的左边界想再往里扩展,右侧阴影左边字符p与左侧阴影右边字符n是一样的,仍关于Po对称,p=n,而边界之外(左阴影左m,右阴影右q)的字符则是一定不同的,否则len[Po]还能更大,m≠q。但m,n是对称的,m=n,所以p≠q。
所以如果i+len[j]严格大于mx,len[i]=mx-i。一定的。
但如果恰好边界重合了,j虽然扩不出去了,但i还有可能。因为m,q一定是不一样的,m,n也不一样,n,p一样。
q≠m≠n=p,p,q可能相等。这时候边界以外就要好好在扩张一遍,mx外面可能还有i的回文串,别忘了更新Po,mx。
情况二:
i > mx

啥也不用说了,已经得到的信息卵用没有,老实儿的重新枚举扩展。
这部分的代码:
void manacher(int n){
int mx=0,po=0;
for(int i=1;i<n*2;i++){
if(mx>i&&i+f[po*2-i]<mx){
f[i]=f[po*2-i];
continue;
}
else if(mx>i&&i+f[po*2-i]>=mx){
f[i]=mx-i;
if(i+f[po*2-i]>mx)continue;
}
else f[i]=1;
while(check(i-f[i],i+f[i]))
f[i]++;
if(f[i]+i>mx)
mx=f[i]+i,po=i;
}
}
按原意写的代码。但是代码长度还可以缩减,因为即使len[i]=len[j]或者len[i]=mx-i没跑了,放在枚举扩展的while循环里也就是判断一下,就跳出来了。都放在一起,取一下最小值,这样mx > i下的三种情况就不用另行区分了。我测验在1e6范围下时间上也就多不到10ms。可以说不值一提了。代码简略了,考场出错概率也就小了。如下:
void manacher(int n){
int mx=0,po=0;
for(int i=1;i<n*2;i++){
if(mx>i)
f[i]=min(f[po*2-i],mx-i);
else f[i]=1;
while(s[i-f[i]]==s[i+f[i]])
f[i]++;
if(f[i]+i>mx)
mx=f[i]+i,po=i;
}
}
总结
这方面的题还是比较好做,不用涉及太多其他的算法。
最多是在字符串上跑动归,不过出题人想难为我们蒟蒻我们也做不上哈
原稿中间出了些错误改了大半天而且原创,比我借鉴的原文要详细,希望支持~
2017-08-22更


