浅谈矩阵

矩阵

P1939 矩阵加速（数列）

P1939 【模板】矩阵加速（数列）

已知一个数列 $a$ ，它满足：

a_x=\begin{cases}1&&x\in [1,2,3]\\ a_{x-1}+a_{x-3}&& x\le4\end{cases}

求 $a$ 数列的第 $n$ 项对 $10^9+7$ 取余的值。

sol

设 $F_0=\begin{bmatrix}f_1 & f_2 & f_3\end{bmatrix}=\begin{bmatrix}1&1&1\end{bmatrix}$ 。

那么有：

F_1=\begin{bmatrix}f_4 & f_5 & f_6\end{bmatrix}=F_0 \times A=\begin{bmatrix}f_1 & f_2 & f_3 \end{bmatrix}\times \begin{bmatrix}1&1&1\\0&1&1\\1&1&2\end{bmatrix}

#include <bits/stdc++.h>
using namespace std;

#define int unsigned long long

const int mod = 1e9 + 7;

int T, n = 3, k;

struct juzhen
{
	int a[4][4];
	juzhen()
	{
		memset(a, 0, sizeof a);
	}
};

juzhen operator * (const juzhen &a, const juzhen &b)
{
	juzhen z;
	for(int k = 1; k <= n; ++k)
		for(int i = 1; i <= n; ++i)
			for(int j = 1; j <= n; ++j)
				z.a[i][j] = (z.a[i][j] + a.a[i][k] * b.a[k][j] % mod) % mod;
	return z;
}

signed main()
{
	scanf("%lld", &T);
	while(T--)
	{
		scanf("%lld", &k);
		juzhen a, ans;
		if (k <= 3)
		{
			puts("1");
			continue;
		}
		a.a[1][1] = a.a[1][3] = a.a[2][1] = a.a[3][2] = 1;
		ans.a[1][1] = ans.a[2][2] = ans.a[3][3] = 1;
		while(k)
		{
			if(k & 1)
			{
				ans = ans * a;
			}
			a = a * a;
			k >>= 1;
		}
		printf("%lld\n", ans.a[2][1]);
	}
	return 0;
}

P1962 斐波那契数列

$f_n=\begin{cases}1 &&(n \le 2)\\f_{n-1}+f_{n-2} && (n\ge 3) \end{cases}$

求 $f_n \bmod 10^9+7$ 的值。

sol

设 $F_0=\begin{bmatrix}f_0 &f_1\end{bmatrix}=\begin{bmatrix}0 & 1\end{bmatrix}$ 。

那么有：

F_1=\begin{bmatrix}f_1&f_2\end{bmatrix}=F_0 \times A=\begin{bmatrix}f_0 &f_1\end{bmatrix} \times \begin{bmatrix}0 & 1\\1&1\end{bmatrix}

#include <bits/stdc++.h>
using namespace std;

#define int long long

const int _ = 10;

const int mod = 1e9 + 7;

int n = 2, k;

struct juzhen
{
	int a[_][_];
	juzhen()
	{
		memset(a, 0, sizeof a);
	}
};

juzhen operator * (const juzhen &a, const juzhen &b)
{
	juzhen z;
	for(int k = 1; k <= n; ++k)
		for(int i = 1; i <= n; ++i)
			for(int j = 1;j <= n; ++j)
				z.a[i][j] = (z.a[i][j] + a.a[i][k] * b.a[k][j] % mod) % mod;
	return z;
}

signed main()
{
	scanf("%lld", &k);
	juzhen a, ans;
	a.a[1][1] = a.a[1][2] = a.a[2][1] = 1;
	ans.a[1][1] = ans.a[1][2] = 1;
	if (k <= 2) return puts("1"), 0;
	k -= 2;
	while(k)
	{
		if(k & 1)
		{
			ans = ans * a;
		}
		a = a * a;
		k >>= 1;
	}
	printf("%lld\n", ans.a[1][1]);
	return 0;
}

P1349 广义斐波那契数列

广义的斐波那契数列是指形如 $a_n=p\times a_{n-1}+q\times a_{n-2}$ 的数列。

今给定数列的两系数 $p$ 和 $q$ ，以及数列的最前两项 $a_1$ 和 $a_2$ ，另给出两个整数 $n$ 和 $m$ ，试求数列的第 $n$ 项 $a_n \bmod m$ 。

sol

$f_n=p\times f_{n-1}+q \times f_{n-2}$

设 $F_0=\begin{bmatrix}f_0 &f_1\end{bmatrix}=\begin{bmatrix}a_1&a_2\end{bmatrix}$ 。

那么有：

F_1=\begin{bmatrix}f_1 &f_2\end{bmatrix}=F_0\times A=\begin{bmatrix}f_0 & f_1\end{bmatrix}\times \begin{bmatrix}0 & q\\1 & p\end{bmatrix}

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2;
int n, m, k, mod, p, q, a1, a2;

void mul(int c[], int a[], int b[][N])
{
	int tmp[N] = {0};
	for(int j = 0; j < N; ++ j)
	{
		for(int k = 0; k < N; ++ k)
		{
			tmp[j] = (tmp[j] + a[k] * b[k][j]) % mod;
		}
	}
	memcpy(c, tmp, sizeof tmp);
}

void mul(int c[][N], int a[][N], int b[][N])
{
	int tmp[N][N] = {0};
	for(int i = 0; i < N; ++ i)
	{
		for(int j = 0; j < N; ++ j)
		{
			for(int k = 0; k < N; ++ k)
			{
				tmp[i][j] = (tmp[i][j] + a[i][k] * b[k][j]) % mod;
			}
		}
	}
	memcpy(c, tmp, sizeof tmp);
}


signed main()
{
	scanf("%lld%lld%lld%lld%lld%lld", &p, &q, &a1, &a2, &n, &m);
	mod = m;
	int f[N];
	f[0] = a1;
	f[1] = a2;
	int a[N][N] =
	{
		{0, q},
		{1, p},
	};
	n --;
	while(n)
	{
		if(n & 1) mul(f, f, a);
		mul(a, a, a);
		n >>= 1;
	}
	printf("%lld\n", f[0]);
	return 0;
}

CF185A Plant

Dwarfs 种了一株非常有意思的植物，这株植物像一个方向向上的三角形。

它有一个迷人的特点，那就是在一年后一株方向向上的三角形的植物就会被分成 $4$ 株三角形的植物：它们当中的三株方向是向上的，一株方向是向下的。

又一年之后，每株植物都会分成四个，规则如上。

之后的每年都会重复这一过程。

下面的图说明了这一发展过程。

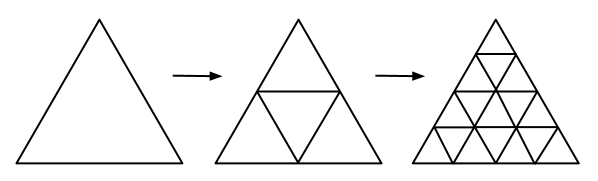
请帮助 Dwarfs 算出 $n$ 年后方向向上的三角形的个数 $\bmod 10^9+7$ 的值。

sol

设 $f_{i,0}$ 为 $i$ 年后向上的三角形的个数， $f_{i,1}$ 为 $i$ 年后向下的三角形的个数，则我们可以得到以下的递推式：

f_{i,0}=f_{i-1,0} \times 3+f_{i-1,1}\\ f_{i,1}=f_{i-1,1}\times 3+f_{i-1,0}

初始为 $f_{0,0} = 1$ ， $f_{0,1} = 0$ 。

根据上面的递推式，我们可以得到：

\begin{bmatrix}f_{i-1,0}& f_{i-1,1}\end{bmatrix}\times\begin{bmatrix}3 &1\\1 &3\end{bmatrix}=\begin{bmatrix}f_{i,0}&f_{i,1}\end{bmatrix}

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

const ll mod = 1000000007;

ll n;
struct matrix
{
	int n;
	ll a[110][110];
} a;

matrix mul(matrix &a, matrix &b)
{
	matrix res;
	res.n = a.n;
	memset(res.a, 0, sizeof(res.a));
	for (int i = 1; i <= res.n; ++i)
	{
		for (int j = 1; j <= res.n; ++j)
		{
			for (int k = 1; k <= res.n; ++k)
			{
				res.a[i][j] = (res.a[i][j] + a.a[i][k] * b.a[k][j]) % mod;
			}
		}
	}
	return res;
}

matrix qpow(matrix a, ll p)
{
	matrix res;
	res.n = a.n;
	memset(res.a, 0, sizeof(res.a));
	res.a[1][1] = 1;
	while (p)
	{
		if (p & 1)
		{
			res = mul(res, a);
		}
		a = mul(a, a);
		p >>= 1;
	}
	return res;
}

signed main()
{
	scanf("%lld", &n);
	a.n = 2;
	a.a[1][1] = a.a[2][2] = 3;
	a.a[1][2] = a.a[2][1] = 1;
	matrix ans = qpow(a, n);
	printf("%lld", ans.a[1][1]);
	return 0;
}

P4000 斐波那契数列

$f_n=\begin{cases}1 &&(n \le 2)\\f_{n-1}+f_{n-2} && (n\ge 3) \end{cases}$

求 $f_n \bmod p$ 的值。

$n\leq 10^{30000000},p<2^{31}$ 。

sol

这题肯定不能暴力算。

找循环节，不用最小，够小就行了。

有 $\pi(p) \leq 6\times q$ ，用随机化加 unordered_map 判断之前是否有出现过即可。

参考

#include<bits/stdc++.h>
using namespace std;

#define ll long long
#define ull unsigned long long
unordered_map < ull , ll > circ;
ll len;
int MOD , MX = 1 << 18;
mt19937_64 rnd(time(0));
struct matrix
{
	ll arr[2][2];
	matrix()
	{
		memset(arr , 0 , sizeof(arr));
	}
	ll* operator [](int x)
	{
		return arr[x];
	}
	friend matrix operator *(matrix p , matrix q)
	{
		matrix x;
		for(int i = 0 ; i < 2 ; ++i)
			for(int j = 0 ; j < 2 ; ++j)
				for(int k = 0 ; k < 2 ; ++k)
					x[i][k] += p[i][j] * q[j][k];
		for(int i = 0 ; i < 2 ; ++i)
			for(int j = 0 ; j < 2 ; ++j) x[i][j] %= MOD;
		return x;
	}
} G , T[2][1 << 18 | 1];

signed main()
{
	static char str[300000003];
	scanf("%s %d" , str + 1 , &MOD);
	T[0][0][0][0] = T[0][0][1][1] = T[1][0][0][0] = T[1][0][1][1] = 1;
	T[0][1][0][1] = T[0][1][1][0] = T[0][1][1][1] = 1;
	for(int i = 2 ; i <= MX ; ++i) T[0][i] = T[0][i - 1] * T[0][1];
	T[1][1] = T[0][MX];
	for(int i = 2 ; i <= MX ; ++i) T[1][i] = T[1][i - 1] * T[1][1];
	while(1)
	{
		ll x = (rnd() << 28 >> 28);
		matrix C = T[0][x & (MX - 1)] * T[1][x >> 18];
		ull val = ((1ull * C[0][0]) << 32) | C[0][1];
		if(circ.find(val) != circ.end())
		{
			len = abs(circ[val] - x);
			break;
		}
		circ[val] = x;
	}
	ll sum = 0;
	for(int i = 1 ; str[i] ; ++i) sum = (sum * 10 + str[i] - '0') % len;
	cout << (T[0][sum & (MX - 1)] * T[1][sum >> 18])[0][1];
	return 0;
}

P4838 P哥破解密码

定义一个串合法，当且仅当串只由 A 和 B 构成，且没有连续的3个 A。

P 哥知道，密码就是长度为 $N$ 的合法字符串数量对 $19260817$ 取模的结果。

但是P哥不会算，所以他只能把 $N$ 告诉你，让你来算。

至于为什么要对这个数取模，好像是因为纪念某个人，但到底是谁，P 哥也不记得了。

$M$ 组数据。

sol

令 $f_{n,x}$ 表示串长度为 $n$ ，且从 $n$ 位置向左有 $x$ 个连续的 A，字串的方案数。

不难看出 $1\le n\le N, 0\le x\le 2$ 。

当 $x=0$ 时，从 $n-1$ 位置往左走显然有 $0,1,2$ 个，不管多少个都不会改变最后一位是 B 的事实，所以有：

f_{n,0}=f_{n-1,0}+f_{n-1,1}+f_{n-1,2}

当 $x=1$ 时，从 $n-1$ 位置往左数不应该有 A，故：

f_{n,1}=f_{n-1,0}

同理，有：

f_{n,2}=f_{n-1,1}

初始条件显然为：

\begin{cases}f_{0,0}=1\\f_{0,1}=0\\ f_{0,2}=0\end{cases}

答案显然为 $f_{N,0}+f_{N,1}+f_{N,2}$ 。

显然，又有：

\begin{bmatrix}f_{n,2}&f_{n,1}&f_{n,0}\end{bmatrix} \times \begin{bmatrix}0&0&1\\1&0&1\\0&1&1\end{bmatrix}=\begin{bmatrix}f_{n+1,2}&f_{n+1,1}&f_{n+1,0}\end{bmatrix}

那么，有：

\begin{bmatrix}f_{0,2}&f_{0,1}&f_{0,0}\end{bmatrix}\times \begin{bmatrix}0&0&1\\1&0&1\\0&1&1\end{bmatrix}^N=\begin{bmatrix}f_{N,2}&f_{N,1}&f_{N,0}\end{bmatrix}

#include <bits/stdc++.h>

using namespace std;

#define int long long

inline int read()
{
	int x = 0, f = 1;
	char c = getchar();
	while(c < '0' || c > '9')
	{
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9')
	{
		x = x * 10 + c - '0';
		c = getchar();
	}
	return x * f;
}

const int _ = 4;

const int mod = 19260817;

int T, n, k;

struct juzhen
{
	int a[_][_];
	juzhen()
	{
		memset(a, 0, sizeof a);
	}
};

juzhen operator * (const juzhen &a, const juzhen &b)
{
	juzhen z;
	for(int k = 1; k <= 3; ++k)
		for(int i = 1; i <= 3; ++i)
			for(int j = 1;j <= 3; ++j)
				z.a[i][j] = (z.a[i][j] + a.a[i][k] * b.a[k][j] % mod) % mod;
	return z;
}

const int GE[4][4] = 
{
	{-1, -1, -1, -1},
	{-1, 0, 0, 1},
	{-1, 1, 0, 1},
	{-1, 0, 1, 1},
};

int tmp[4] = {0, 0, 0, 1}, res[4];

signed main()
{
	T = read();
	while(T--)
	{
		n = read();
		juzhen a, ret;
		for(int i = 1; i <= 3; ++i)
			for(int j = 1; j <= 3; ++j)
				a.a[i][j] = GE[i][j];
		for(int i = 1; i <= 3; ++i)
			ret.a[i][i] = 1;
		while(n)
		{
			if(n & 1) ret = ret * a;
			a = a * a;
			n >>= 1;
		}
		memset(res, 0, sizeof res);
		for(int i = 1; i <= 1; ++i)
			for(int j = 1; j <= 3; ++j)
				for(int k = 1; k <= 3; ++k)
					res[j] = (res[j] + tmp[k] * ret.a[k][j] % mod) % mod;
		printf("%lld\n", (res[1] + res[2] + res[3]) % mod);
	}
	return 0;
}

P5678 [GZOI2017]河神

Shlw 从河神给的选择中，获得了一道当年挂掉的代数题的灵感。

但现在他希望你来帮忙解答，因为他自己忙着去搜小马资源去了。

给出数列 $\{a_n\}$ 和 $\{b_n\}$ 以及 $\{A_n\}$ 的递推关系，试求出数列 $\{A_n\}$ 第 $N$ 项。

递推关系为：

sol

考虑用矩阵快速幂来解决，此处我们更改矩阵乘法的定义：将原本的乘法改为按位与，原本的加法改为按位或。

那么，有：

\begin{bmatrix}a_{n-1}&a_{n-2}&\cdots&a_{n-k}\end{bmatrix}\times \begin{bmatrix}b_1&+\infty &0&\cdots&0\\b_2&0&+\infty&\cdots &0\\b_3 &0&0&\cdots&0\\\cdots&\cdots&\cdots&\cdots&\cdots\\b_{k-1}&0&0&\cdots&+\infty\\b_k&0&0&\cdots&0\end{bmatrix}=\begin{bmatrix}a_n&a_{n-1}&\cdots&a_{n-k+1}\end{bmatrix}

这里的 $+\infty$ 指的是二进制中每一位都是 $1$ 的数。

#include <bits/stdc++.h>

#define N 105

#define ll long long

using namespace std;

ll read()
{
	ll x = 0, f = 0;
	char c = getchar ();
	while(c < '0' || c > '9') f = c == '-', c = getchar ();
	while(c >= '0' && c <= '9') x = (x << 1) + (x << 3) + (c ^ 48), c = getchar ();
	return f ? - x : x;
}

const ll maxx = (1ull << 63) - 1;

int n, k;

ll a[N], b[N];

struct Matrix
{
	int n, m;
	ll a[N][N];
	friend Matrix operator * (const Matrix & x, const Matrix & y)   // 定义矩阵乘法
	{
		Matrix ret;
		ret.n = x.n, ret.m = y.m;
		for(int i = 1; i <= x.n; i ++)
			for(int j = 1; j <= y.m; j ++)
				for(int k = 1; k <= x.m; k ++)
					ret.a[i][j] |= x.a[i][k] & y.a[k][j];
		return ret;
	}
	Matrix()
	{
		n = m = 0;
		memset (a, 0, sizeof a);
	}
} mat0, mat1;

Matrix ksm(Matrix x, int y)
{
	Matrix ret = x;
	y--;
	while(y)
	{
		if(y & 1) ret = ret * x;
		x = x * x;
		y >>= 1;
	}
	return ret;
}

signed main()
{
	n = read(), k = read();
	for(int i = 1; i <= k; ++i) a[i] = read();
	for(int i = 1; i <= k; ++i) b[i] = read();
	if(n <= k)
	{
		printf ("%lld\n", a[n]);
		return 0;
	}
	mat1.n = mat1.m = k;
	for(int i = 1; i <= k; ++i)
		mat1.a[i][1] = b[k - i + 1];
	for(int i = 1; i < k; ++i)
		mat1.a[i][i + 1] = maxx;
	mat0.n = 1, mat0.m = k;
	for(int i = 1; i <= k; ++i)
		mat0.a[1][i] = a[k - i + 1];
	Matrix ans = mat0 * ksm (mat1, n - k + 1);
	printf("%lld\n", ans.a[1][1]);
	return 0;
}

P4967 黑暗打击

有一群生物 ccj，他们在上次的星系中，发现了一群低等生物，于是想进行一波黑暗森林打击。

这群低等生物即是 $\mathsf{Hilbert}$ 鼹鼠，生活在 $\mathsf{Hilbert}$ 星球，住在 $\mathsf{Hilbert}$ 曲线土壤内。

这群生物决定用最傻的办法——灌水，来淹死他们。现在“高等”生物想知道，对于 $n$ 阶的 $\mathsf{Hilbert}$ 曲线，从上往下灌水，能淹没几个单位面积？

这是 $1 \sim 4$ 阶的 $\mathsf{Hilbert}$ 曲线：

$h_1$ ，如最左图所示，是一个缺上口的正方形，这个正方形的边长为 $1$ 。

从 $h_2$ 开始，按照以下方法构造曲线 $h_i$ ：将 $h_{i-1}$ 复制四份，按 $2\times2$ 摆放。

把左上一份逆时针转 $90^{\circ}$ ，右上一份顺时针转 $90^{\circ}$ ，然后用三条单位线段将四分曲线按照左上-左下-右下-右上的顺序连接起来。

如图所示，分别展示的是 $h_2$ ， $h_3$ ， $h_4$ 。

加粗的线段是额外用于连接的线段。

灌水方式：

（显然这个是 $h_3$ 的灌水面积）绿色即为无法被灌到的地方，红色为可以灌到的地方，灰色为墙，所以答案是 $26$ ，即为样例 $1$ 。

一个方格有水当且仅当在它的上，左，右方格中有至少一个方格有水，最上面一层的空格都有水。

注，此题要求对 $9223372036854775783$ 取模

$n \leq 10^{10000}$ 。

sol

设 $n$ 阶图形灌水面积为 $f(n)$ ， $n$ 阶图形旋转 $90^{\circ}$ 灌水面积为 $g(n)$ 。

则有：

f(n)=2\times f(n-1)+2\times g(n-1)+2^{n-1}-1+2^n-1

和：

g(n)=f(n-1)+2\times g(n-1)+2^{n-1}-1

显然，公式中涉及 $f(n),g(n),2^n,1$ 。

故设 $F(n)=\begin{bmatrix}f(n)&g(n)&2^n &1\end{bmatrix}$ 。

那么有：

F(n)=A \times F(n-1)=A\times \begin{bmatrix}f(n-1) & g(n-1) &2^{n-1}& 1\end{bmatrix}=\begin{bmatrix}2 & 1 & 0 & 0\\2&2&0&0\\3&1&2&0\\-2&-1&0&1\end{bmatrix}\times \begin{bmatrix}f(n-1) & g(n-1) &2^{n-1} & 1\end{bmatrix}

因为 $f(1)=1,g(1)=1,2^1=2$ 。

那么有：

F(n)=\begin{bmatrix}f(n) & g(n) &2^n &1\end{bmatrix}=F(1) \times A^{n-1}=\begin{bmatrix}1&1&2&1\end{bmatrix}\times A^{n-1}

单纯用矩阵快速幂的话时间复杂度为 $\mathcal O(\log n)$ ，过不去。

考虑扩展欧拉定理缩小指数部分：

a^b\equiv \begin{cases} a^b & b<\varphi(p)\\ a^{b \ \bmod \ \varphi(p) + \varphi(p)} & b\geq\varphi(p) \end{cases} \pmod p

这里就不证了，证明可看我的博客欧拉函数与（扩展）欧拉定理。

#include<bits/stdc++.h>

using namespace std;

#define int __int128

const int mod = 9223372036854775783ll, phi = (mod - 1ll);

const int N = 4;

bool flag;

int n;

int js(int x, int mod)
{
	if(x < mod) return x;
	return x % mod + mod;
}

int read()
{
	int x = 0, f = 1;
	char ch = getchar();
	while(ch < '0' || ch > '9')
	{
		if(ch == '-') f = -1;
		ch = getchar();
	}
	while(ch >= '0' && ch <= '9')
	{
		x = x * 10 + ch - '0';
		x = js(x, phi);
		ch = getchar();
	}
	return x * f;
}

void write(int x)
{
	if(x < 0)
	{
		putchar('-');
		x = -x;
	}
	if(x > 9) write(x / 10);
	putchar(x % 10 + '0');
}

struct Matrix
{
	int a[N][N];
	Matrix()
	{
		memset(a, 0, sizeof a);
	}
};

Matrix mul(Matrix a, Matrix b)
{
	Matrix tmp;
	for(int i = 0; i < N; ++ i)
		for(int j = 0; j < N; ++ j)
			for(int k = 0; k < N; ++ k)
				tmp.a[i][j] = (tmp.a[i][j] + a.a[i][k] * b.a[k][j]) % mod;
	return tmp;
}

int q[N] = {1, 0, 2, 1};

int z[N][N] =
{
	{2, 1, 0, 0},
	{2, 2, 0, 0},
	{3, 1, 2, 0},
	{-2, -1, 0, 1}
};

signed main()
{
	n = read() - 1;
	Matrix a, f;
	for(int i = 0; i < N; ++i)
		for(int j = 0; j < N; ++j)
			a.a[i][j] = z[i][j];
	for(int j = 0; j < N; ++j)
		f.a[0][j] = q[j];
	while(n)
	{
		if(n & 1) f = mul(f, a);
		a = mul(a, a);
		n >>= 1;
	}
	write(f.a[0][0]);
	putchar('\n');
	return 0;
}

P5136 sequence

求：

\left\lceil\left(\frac{1+\sqrt{5}}{2}\right)^{i}\right\rceil

sol

首先考虑将原式转换为：

\left\lceil\left(\frac{1+\sqrt{5}}{2}\right)^{i}+\left(\frac{1-\sqrt{5}}{2}\right)^{i}-\left(\frac{1-\sqrt{5}}{2}\right)^{i}\right\rceil

显然有：

\left(\frac{1+\sqrt{5}}{2}\right)^{i}+\left(\frac{1-\sqrt{5}}{2}\right)^{i}=f(i)

其中 $f$ 为斐波那契数列。

考虑用矩阵快速幂优化递推计算。

显然，设状态矩阵为：

\begin{bmatrix}f_{n}&f_{n-1}\end{bmatrix}

显然，转移矩阵为：

\begin{bmatrix}1&1\\1&0\end{bmatrix}

最后再来看看减去的 $\left(\frac{1-\sqrt{5}}{2}\right)^{i}$ 对最终答案的影响。

考虑分奇偶性讨论：

当 $i$ 为偶数时， $-\left(\frac{1-\sqrt{5}}{2}\right)^{i}$ 为负，无影响。
当 $i$ 为奇数时， $-\left(\frac{1-\sqrt{5}}{2}\right)^{i}$ 为正，最终答案加一。

那就没了。。。

#include <bits/stdc++.h>

using namespace std;

#define int long long

inline int read()
{
    int x = 0, f = 1;
    char c = getchar();
    while (c < '0' || c > '9')
    {
        if (c == '-')
            f = -1;
        c = getchar();
    }
    while (c >= '0' && c <= '9')
    {
        x = x * 10 + c - '0';
        c = getchar();
    }
    return x * f;
}

int T, n;

const int MOD = 998244353;

struct mat
{
    int a[2][2];
    mat()
    {
        memset(a, 0, sizeof a);
    }
    mat operator*(const mat &b) const
    {
        mat op;
        for (int i = 0; i < 2; i++)
            for (int k = 0; k < 2; k++)
                for (int j = 0; j < 2; j++)
                    op.a[i][j] = (op.a[i][j] + a[i][k] * b.a[k][j]) % MOD;
        return op;
    }
} ans, I;

void init()
{
    I.a[0][0] = I.a[0][1] = I.a[1][0] = 1;
    I.a[1][1] = 0;
    ans.a[0][0] = 3, ans.a[0][1] = 1;
    ans.a[1][0] = ans.a[1][1] = 0;
}

signed main()
{
    T = read();
    while (T--)
    {
        n = read();
        init();
        if (n == 0)
        {
            printf("1\n");
            continue;
        }
        else if (n == 1)
        {
            printf("2\n");
            continue;
        }
        bool flag = 0;
        if(n % 2 == 1) flag = 1;
        n -= 2;
        while (n)
        {
            if (n & 1)
                ans = ans * I;
            I = I * I;
            n >>= 1;
        }
        printf("%lld\n", ans.a[0][0] + flag);
    }
    return 0;
}

[JLOI2015]有意义的字符串

求：

\left\lfloor\left(\frac{b+\sqrt{d}}{2}\right)^{n}\right\rfloor \pmod{7528443412579576937}

其中 $0<b^2 \le d<(b+1)^2 \le 10^{18},n \le 10^{18}$ ，并且 $b \bmod 2=1,d \bmod 4=1$ 。

先将上述式子变为：

\left\lfloor\left(\frac{b+\sqrt{d}}{2}\right)^{n}\right\rfloor +\left\lfloor\left(\frac{b-\sqrt{d}}{2}\right)^{n}\right\rfloor - \left\lfloor\left(\frac{b-\sqrt{d}}{2}\right)^{n}\right\rfloor

设 $x=\frac{b+\sqrt{d}}{2},y=\frac{b-\sqrt{d}}{2}$ 。

设 $f_n=x^n+y^n$ 。

设状态矩阵为：

\begin{bmatrix}f_n & f_{n-1}\end{bmatrix}

考虑将 $f_n$ 拆成 $? \times f_{n-1} - ? \times f_{n-2}$ 的形式，又因为 $f_{n-1}=x^{n-1}+y^{n-1}$ ， $f_{n-2}=x^{n-2}+y^{n-2}$ ，代入得：

?\times \left(x^{n-1}+y^{n-1}\right)-? \times \left(x^{n-2}+y^{n-2}\right)

于是稍加考虑就可以得出：

x^n+y^n=(x+y)\times(x^{n-1}+y^{n-1})-xy\times(x^{n-2}+y^{n-2})

所以递推式为：

f_n=(x+y)\times f_{n-1}-xy\times f_{n-2}

然后根据题目给的信息，易证 $f_n$ 为整数。

所以转移矩阵为：

\begin{bmatrix}b&1\\-\frac{b^2-d}{4}&0\end{bmatrix}

最后再来看看最后减去的 $\left\lfloor\left(\frac{b-\sqrt{d}}{2}\right)^{n}\right\rfloor$ 对答案的影响：

由于答案是向下取整，所以当 $-\left\lfloor\left(\frac{b-\sqrt{d}}{2}\right)^{n}\right\rfloor$ 为正且大小在区间 $\left[ 0,1 \right)$ 时对答案无影响。

由于 $0<b^2 \le d<(b+1)^2 \le 10^{18}$ ，所以 $\left\lfloor\left(\frac{b-\sqrt{d}}{2}\right)^{n}\right\rfloor$ 的范围一定在 $\left[0,1\right)$ 内。

接下来只要讨论式子的正负性。

因为 $0<b^{2} \le d$ ，所以 $\frac{b-\sqrt{d} }{2}$ 一定小于 $0$ 。

当 $n \bmod{2}=1$ 时，即 $n$ 为奇数时， $-\left ( \frac{b-\sqrt{d} }{2} \right )^{n}$ 范围一定在 $\left [ 0,1 \right )$ 内，对答案没有影响。

相反，当 $n \bmod{2}=0$ 时， $-\left ( \frac{b-\sqrt{d} }{2} \right )^{n}$ 的范围在区间 $\left ( -1,0 \right ]$ 内。

当式子等于 $0$ 时，即 $b=\sqrt{d}$ ， $b^{2}=d$ 时，该式对答案无影响。

综上，当且仅当 $n$ 为偶数且 $b^{2}\ne d$ 时，该式对答案有影响，答案向下取整后的值需要减一。

#include <bits/stdc++.h>

using namespace std;

#define int long long

#define ull unsigned long long

inline int read()
{
	int x = 0, f = 1;
	char c = getchar();
	while(c < '0' || c > '9')
	{
		if(c == '-') f = -1;
		c = getchar();
	}
	while(c >= '0' && c <= '9')
	{
		x = x * 10 + c - '0';
		c = getchar();
	}
	return x * f;
}

const int MOD = 7528443412579576937;

int b, d, n;

int mul(int a, int k) 
{
	ull ans = 0;
	while (k) 
	{
		if (k & 1) ans = (ans + a) % MOD;
		a = (ull)(a + a) % MOD;
		k >>= 1;
	}
	return ans;
}

struct mat 
{
	int a[2][2];
	mat() { memset(a, 0, sizeof a); }
	mat operator * (const mat &b) const 
	{
		mat op;
		for (int i = 0; i < 2; i++) 
			for (int k = 0; k < 2; k++) 
				for (int j = 0; j < 2; j++) 
					op.a[i][j] = (ull)(op.a[i][j] + mul(a[i][k], b.a[k][j])) % MOD;  //ull
		return op;
	}
} ans, I;

void init() 
{
	I.a[0][0] = b, I.a[0][1] = 1, I.a[1][0] = (d - b * b) / 4;
	ans.a[0][0] = (b * b + d) / 2, ans.a[0][1] = b;
}

signed main() 
{
	b = read(), d = read(), n = read();
	init();
	if (n == 0ll) 
	{
		printf("1");
		return 0;
	} else if (n == 1ll) 
	{
		printf("%lld ", (int)((b + sqrt(d)) / 2) % MOD);
		return 0;
	}
	n -= 2;
	int ff = 0;
	if (b * b != d && n % 2 == 0) ff--;
	while (n) 
	{
		if (n & 1)ans = ans * I;
		I = I * I;
		n >>= 1;
	}
	ans.a[0][0] += ff;
	printf("%lld ", ans.a[0][0]);
	return 0;
}

posted @ 2021-12-18 09:13 蒟蒻orz 阅读(9) 评论(0) 编辑收藏举报来源

刷新页面返回顶部

蒟蒻orz

浅谈矩阵

矩阵

P1939 矩阵加速（数列）

sol

P1962 斐波那契数列

sol

P1349 广义斐波那契数列

sol

CF185A Plant

sol

P4000 斐波那契数列

sol

P4838 P哥破解密码

sol

P5678 [GZOI2017]河神

sol

P4967 黑暗打击

sol

P5136 sequence

sol

[JLOI2015]有意义的字符串

公告