2023/11 训练

合集 - 做题记录(8)

1.2023/11 训练2024-04-08

2.2024 1/2 成七训练2024-04-083.3月记录2024-03-094.4月记录2024-04-085.5、6月记录2024-05-096.7月记录2024-07-047.8月记录2024-08-018.9月记录2024-09-03

收起

AT_arc165_d [ARC165D] Substring Comparison

考虑字典序的性质。

我们维护当前的 $a_i,c_i$ 表示判断 $a_i$ 是否 $<c_i$，连边。

tarjan 判环，如果是一个环，说明环上所有点都相等。

注意，我们连边是对两个点的环进行连边。

对于一个限制，如果当前的 $a_i,c_i$ 都在环上，即前缀都相等，那么 $a_i,c_i$ 都往下跳一位，说明我们判断下一位的关系。

最后跑完某个区间判断有无解即可。

如果 tarjan 时没有新的环合并，那么结束。

AT_arc165_e [ARC165E] Random Isolation

什么神仙。

将期望转到局面上。

发现期望相当于每个还可以操作的局面出现的概率之和。

于是我们找到局面，算概率即可。

找到树上一个大小为 $a$ 的子图，满足 $a>k$，如果有 $b$ 个之外的点与之相连。

我们考虑将操作的序列看成排列，那么出现这种局面的概率为 $\frac{a!b!}{(a+b)!}$，因为这 $b$ 个数都得在 $a$ 的前面，相对关系确定了。

然后树上背包转移即可，令 $f_{u,i,j}$ 表示只考虑 $u$ 的子树内的点，$u$ 在子树内的联通块大小为 $i$，与之相连的点有 $j$ 个的方案数。

AT_arc108_f [ARC108F] Paint Tree

发现同颜色最远点对一定有一点在直径 $S$ 上。

这下找到直径，算每个点到直径的两种距离。

然后枚举最远点对长度 $d$，根据两种距离跟 $d$ 的大小关系，我们可以知道一个点选的方案数。

然后我们考虑容斥。

记答案为 $\sum w_if_i$ 的形式，表示最远点对为 $w_i$ 的方案数为 $f_i$。

对于一个 $x$，我们计算 $g(x)=\sum [w_i> x]f_i$，则答案为 $\sum\limits_{x=0}^{S-1} g(x)$。

我们钦定直径的颜色不同。

记 $mn=\max(\min(d1_i,d2_i))$，即最远点对的最小值。

对于 $x\in [0,mn)$，$g(x)=2^n$。

对于 $x\in[mn, S)$，$g(x)=2^n -\sum [w_i\le x]f_i$，减去的就是最远点对 $\le x$ 的方案数。

对于点 $i$，如果它满足 $\max(d1_i,d2_i)\le x$，则它两种颜色都可以染；否则它只能染一种。记满足前者条件的点有 $cnt$ 个，则 $\sum[w_i\le x]f_i=2^{cnt + 1}$，还有对直径颜色的分配。

P9129 [USACO23FEB] Piling Papers G

差分区间。

位数 $\leq len$ 的容易算。

考虑反着来，枚举右端点 $r$，往左推，那么每次就是在前缀的最后和后缀的最前加数，分别维护左右侧和 $x$ 的大小关系就可以转移了。

倒着与正着相比，优势是正着得根据一个确定点来判断大小，而倒着的话，整个序列的形态是固定的。

具体，设 $f_{l,x,y,s,t}$ 表示左端点推到 $l$，左侧与 $x$ 的 $[l,r]$ 相比 $<$，$=$，$>$，右侧同理，的方案数。

做完了。

P9130 [USACO23FEB] Hungry Cow P

考虑每次修改的都是不同的位置，对于一次修改 $a_x=y$，相当于区间覆盖 $[i,k]$，满足这次修改前 $[i,k]$ 中的空位置为 $j$，简单的线段树二分。

对于同一位置的多次修改，我们要让前一次修改对后一次修改没有影响， 就对时间进行线段树分治即可。

发现不好维护撤销，我们就可持久化动态开点线段树。

时间复杂度 $\mathcal O(n\log n\log V )$。

P7218 [JOISC2020] 伝説の団子職人

很像某道题。

将互斥关系之间连边，就是求一般图的最大独立集。

随机了。

随机一个没有用的位置，找到这个位置的所有可能方案，随机选一个，对其他因为这个修改而删除的点加入队列，不断更新，更新的时候不改已经更新多的位置。

CF722F

对于每个权值找出他出现的极长区间，总数是 $\mathcal O(40n)$ 的。

然后我们判断一个区间是否有解，每个限制形如一个同余式，发现模数 $\leq 40$，那么两两判断裴蜀定理即可。

考虑双指针，找到最长合法区间，对每个模数记录出现位置及余数，这很好做。

就做完了。

CF1119F

先暴力贪心。

设 $f_{u,0/1}$ 分别表示是否删除 $u$ 和父亲之间的边，子树内的最小代价。

我们要满足的就是 $u$ 被删除的边数 $k$ 满足 $du_u-k \le x$。

这下每个 $v$，不是选 $w+f_{v,1}$ 就要选 $f_{v,0}$，也就是二选一，且尽量删边。

对于所有儿子 $v$，如果 $f_{v,1}+w_{u,v}\leq f_{v,0}$，那么我们选它是不劣的。

如果我们选了这些后，度数还是无法满足条件。

将未选边按照 $f_{v,1}+w_{u,v}-f_{v,0}$ 排序，从最小开始选就行了。

简化一点，选择前 $du_u-x$ 小的 $f_{v,0}+w_{u,v}$，其他选择 $\min(f_{v,0}+w_{u,v},f_{v,1})$。

$f_{u,1}$ 同理。

发现当 $du_u \leq x$ 时，就是选择了子树内的最优方案，且无需满足度数限制，且 $f_{u,0}$ 和 $f_{u,1}$ 对父亲的影响只有 $w_{u,v}$。

这启发我们，如果我们的可以做到每次只 dp 有用的点，那么复杂度是 $\mathcal O(\sum_x \sum_i [du_i>x])=\mathcal O(\sum du_i)=\mathcal O(n)$。

删掉无用点后，将我们要用到的边权记到有用的点上。

为什么，无用点和无用点之间的边是肯定满足的，那么无用点只会对有用点产生贡献，所以每次相当于将无用点看成联通块无用的叶子。

考虑有用点和无用点之间的决策，能产生影响的就只有 $w_{u,v}$。

CF1553I

排列的单调且连续的区间一定互不相交，且由 $a$ 可以推出这些区间。

如果 $a=\{3,3,3,1,1,1\}$，那么区间就是 $\{[1,3],[4,4],[5,5],[6,6]\}$。

设 $a'$ 表示 $a$ 的相同数连续段长度，那么 $a'=\{3,1,1,1\}$。

将 $[1,n]$ 分配，方案数有 $|a|!$ 种，如上面的例子，如果取数顺序为 $3,1,2,4$，那么区间 $[1,3]$ 分到了 $2,3,4$，可以推出排列 $p$ 为 ${2,3,4,5,1,6}$ 或 ${4,3,2,5,1,6}$。

发现长度 $\ge 2$ 的区间都有两种选择，方案数乘上 $2^x$，$x$ 表示长度 $\ge 2$ 的区间个数。

然后出现问题，我们可能分配出来，使相邻的两个区间组成大区间，考虑把这些情况排除。

容易想到容斥，令 $f_i$ 表示至少 $i$ 对相邻区间合并，那么有：

$$ans=\sum_{i=0}^{len - 1} (-1)^i f(i)$$

分析完了，考虑 dp。

设 $f_{i,j}$ 表示考虑前 $i$ 个区间，并成 $j$ 段的方案数，枚举上一段结束的位置 $l$，若 $i=l+1$ 且 $a'_i=1$，那么 $f_{l,j-1}\to f_{i,j}$；否则 $f_{l,j-1}\times 2\to f_{i,j}$。

最终 $ans=\sum\limits_{i=1}^{m}(-1)^{m-i}i!f_{m,i}$。

前缀和优化可以做到 $\mathcal O(n^2)$。

然后就过了？？？？

容易发现合并段数不能丢，然后如果左边 $x$ 段，右边 $y$ 段，就会合并成 $x+y$ 段，贡献是乘积。

考虑分治 NTT，在中间要处理区间的合并。

CF1889C2 Doremy's Drying Plan (Hard Version)

一开始的想法是将 $k$ 从大到小处理，只会包含 $k$ 的区间，但是当 $k$ 小的时候它还可以选择 $K-k$ 个数。

这下不知怎么办了。

如果单纯地将覆盖每个点的区间作为状态转移的话，根本不行。

考虑对于区间来搞，记 $f_{i,j}$ 表示前 $i$ 个点，我删除的天数包含了所有点 $i$ 的天数，且删了 $j$ 个。

这下只需要处理与点 $i$ 无交集的天数了。

设 $d_t$ 表示区间 $[l,r]$ 的数量，满足 $t<l\le i \le r$，即包含 $i$ 却不包含 $t$ 的区间数量。

考虑转移，我们枚举上一个删掉的点。

$$\max_{t=0}^{i-1}f_{t,j-d_t}+1\to f_{i,j}$$

现在是 $\mathcal O(n^2 k)$。

发现当 $t$ 减小时，$d_t$ 不断增加，但是 $d_t$ 最多只有 $K$ 个，于是我们二分区间，只需要支持区间 $\max$，线段树即可。

时间复杂度 $\mathcal O(kn \log n)$。

CF1889D Game of Stacks

当每个栈只有一个元素时，我们连接 $i\to p_i$，$p_i$ 为第 $i$ 个栈的栈顶。

现在是一棵内向基环树了。

此时询问的答案是每个点对应的树的处在环上的根。

回到原问题，其实我们不断消环，即找到环，将环上的栈顶弹出，并新建连边 $i\to p_i$，并维护每个点的根。

参考代码理解。

int n, tp, st[_], fg[_], vis[_];

stack<int> s[_];

int dfs(int u) {
	if(fg[u]) return fg[u];
	if(s[u].empty()) return u;
	if(vis[u]) {
		while(1) {
			int nw = st[tp];
			--tp;
			s[nw].pop();
			vis[nw] = 0;
			if(nw == u) break;
		}
		return dfs(u);
	}
	st[vis[u] = ++tp] = u;
	return dfs(s[u].top());
}

bool Med;
signed main() {
	// Mry;
	n = ri();
	F(i, 1, n) {
		int k = ri();
		while(k--) {
			int c = ri();
			s[i].push(c);
		}
	}
	F(i, 1, n) {
		tp = 0;
		int ok = dfs(i);
		F(j, 1, tp) fg[st[j]] = ok;
		printf("%d%c", ok, " \n"[i == n]);
	}
	// Try;
	return 0;
}

P9818 游戏王

将 $\lfloor\frac{m}{i}\rfloor$ 相同的看作一个等价类，若 $[l,r]$ 全部等价，则 $[l\times k,r\times k]$ 全部等价。

于是值域变为了 $\sqrt V$。

懂了，不写。

【UR #26】石子合并

首先，对于 $a_i\le a_{i+1}$ 的，发现每个堆里都是不降了，有简单 dp，设 $f_{i,j}$ 表示考虑到第 $i$ 个石子，前面 $j$ 个堆非空，$\mathcal O(n^2m)$。

考虑有下降的石子。

如果第一个石堆里的某个石子 $x$ 后面有一堆比当前石子小的石子，那么当合并时加入 $x$ 后，$x$ 后面一堆编号比 $x$ 小的石子会跟着一起加入，而且仍然保持跟在 $x$ 后面。

因此，我们可以把这些 x 后面比 x 小的石子“归附”到 x 上，容易发现合并过程是不变的！

对于最后合成的序列，当一个石子比前面的任意某个石子小的时候，其一定归附在前面的某个石子上，因此删除其不影响答案！

证明考虑当前是两个堆合并，若存在 $a_k>a_i$ 且 $i$ 不依附任何值，则不可能出现这种情况。

可以扩展到多个堆合并之后的情况。

现在问题就是 $a_i \le a_{i+1}$ 了，考虑优化。

假设现在有 $c_j$ 个石子值为 $j$，要填 $n$ 个堆，堆可以为空，则有：

$$f_n=\prod_{i=1}^{m} \begin{pmatrix}c_j+n-1\\ n\end{pmatrix}$$

再设 $g_n$ 表示堆非空的答案。

则：

$$f_{n}=\sum_k \begin{pmatrix}n\\ k\end{pmatrix}g_k$$

二项式反演，有：

$$g_n =\sum_k (-1)^{n-k} \begin{pmatrix}n \\ k\end{pmatrix} f_k$$

现在是 $\mathcal O(nm)$ 了。

现在要快速算出 $f$。

考虑 $c_j \le 5$ 的部分分，其中 $\begin{pmatrix}c+n-1 \\ c\end{pmatrix}$ 是相同的，考虑合并，记 $t_k=\sum_{j=1}^{m} [c_j=k]$。

有：

$$f_n=\prod_k \begin{pmatrix}k+n-1\\ k\end{pmatrix}^{t_k}$$

我们发现有 $\sum_{k} k\times t_k =m$，即满足 $t_k>0$ 的 $k$ 只有 $\mathcal O(\sqrt m)$ 个。

所以，$\mathcal O(n\sqrt m)$，快速幂的复杂度题解有均摊。

P9747 「KDOI-06-S」签到题

发现操作并不会使一个存在的二进制位消失，所以最后的答案为区间的或。

令这个数为 $mx$，首先序列必须存在 $mx$。

注意到当 $mx$ 出现次数 $\ge 2$ 时，必然有解，可以通过先将这两个数弄成相邻的再左右扩展得到。

现在讨论 $mx$ 出现次数为 $1$ 的情况，我们要把这个数复制成两个数，然后发现，当区间内有不与这个数位置有交的子区间按位或和等于这个数时，满足条件。

发现这东西最优时是一个前缀或一个后缀，通过操作 $(i,r-1,i+1,r)$ 多弄出一个 $mx$。

于是一个区间合法，当且仅当：找到任意一个值为 $mx$ 的位置 $i$，要求 $[1,i−1]$ 或者 $[i+1,n]$ 的或和为 $mx$。

会了，不写。

CSP-S 2023 复赛模拟赛 C. nέο κόsmo

CF1740F Conditional Mix 题解

令 $lim_i$ 表示前 $i$ 大的集合大小总和的最大值，有 $lim_i=\sum_{j=1}^{n}\min(c_j,i)$。

对于一种分配，设其前 $i$ 大的集合大小总和为 $s_i$，则其满足条件的充要条件是 $\forall i\in[1,|s|],s_i\le lim_i$。

我们考虑递减地 dp 序列。

记 $f_{i,j,k}$ 表示填了前 $i$ 个集合，共填了 $j$ 个数，第 $i$ 个集合填了 $k$ 个数。

转移简单，现在是 $\mathcal O(n^3)$。

发现有 $ik\le n$，于是优化到 $\mathcal O(n^2 \log n)$。

铸币(coin)

首先对于两个点 $(u,v)$ 的合并，发现是每 $\gcd(a_u,a_v)$ 个分成一段。

然后点 $u$ 的每一段都会跟点 $v$ 的每一段取或。

在强联通分量内的，两两都会贡献，于是计算其中所有点的 $\gcd$，按这个数将每个点都成 $\bmod \gcd$ 的等价类，每次修改一个等价类，强联通分量中每个点的这个等价类都会变成 $1$，个数容易算。

对于两两强联通分量的边，发现竞赛图缩点后类似链，于是只需要保留拓扑序相邻的点之间的边，共 $\mathcal O(n)$ 条。

转移类似两个点的合并。

分析下复杂度，每次花费 $\mathcal O(\frac{a_i}{\gcd})$ 的复杂度将 $\bmod \gcd$ 的一个等价类全部覆盖成 $1$，只会覆盖 $\mathcal O(\gcd)$ 次，所以复杂度是对的。

CF833E Caramel Clouds & 木府(move)

跟 CF1889C1 很像。

多次询问，我们考虑将每个段的端点标记，将值域分成若干个段。

我们如果可以求出前缀段通过删除能得到的最多空点个数，由于每一段要么全空，要么全被覆盖，所以我们可以二分从而求出答案。

扫描线，找到被覆盖 $\le 2$ 的段，维护到每段区间末尾为止空点的长度 $a_i$，删除至多两个区间后最多空点数 $b_i$，只被第 $i$ 个区间覆盖的长度 $f_i$，则 $b_i=\max(a_i+X)$，其中 $X$ 是这个前缀最多能通过删区间得到多少额外的长度。

删除一个区间的情况不说。

考虑删除两个区间的情况：

• 存在被这两个区间覆盖的段，只有 $\mathcal O(n)$ 个，我们记录只被这两个区间覆盖的长度 $r$，其中 $c_i+c_j\le w$ 的 $f_i+f_j+r_{i,j}$ 可以贡献， 记录 $g_i=\max(f_j,r_{i,j})$，在 $f_i$ 更新时，$f_i+g_i$ 可以贡献。
• 否则，$c_i+c_j\le W$ 的 $f_i+f_j$ 可以贡献，树状数组维护前缀 max 即可。

分类讨论一段被覆盖的情况，首先得满足被 $\le2$ 条线段覆盖：

• 被 $0$ 个区间覆盖，$a_i+len\to a_i$。
• 被 $1$ 个区间覆盖，更新 $f_i$，更新上面两部分的贡献。
• 被 $2$ 个区间覆盖，更新上面第二部分的贡献。

时间复杂度 $\mathcal O((n+m)\log n)$。

CF1237G Balanced Distribution & C: 星琼(star)

搞出平均数 $v$，相当于每个数都得是 $v$，将 $a_i-v\to a_i$，则变成每个数都得为 $0$，且 $a_i \ge -v$。

一个区间能均摊，当且仅当区间和为 $0$。

考虑最小步数，发现上界是 $\lceil\frac{len-1}{k-1}\rceil$ 次。

证明考虑从左往右前 $k$ 个位置。如果我们至少有前缀的和 $\ge 0$，则可以将剩余的数放到第 $k$ 堆，然后按归纳法继续进行。如果我们前缀和 $<0$，则先解决右边的子问题，再解决左边的子问题，相当于每次踢掉 $k-1$ 个数。

考虑这个上取整好像可以贪心，设两个区间的余数分别为 $r1,r2$，考虑合并的变化：

$$\lceil \frac{r1}{k-1}\rceil+\lceil \frac{r2}{k-1}\rceil\to \lceil\frac{r1 + r2 + 1}{k-1}\rceil$$

有 $r1,r2\in [0,k-1)$，$r1+r2+1\in[1,2k-3]$，所以 $\lceil\frac{r1+r2+1}{k-1}\rceil\in[1,2]$，分类讨论：

由上可知，当余数 $\bmod (k-1)\ne 0$ 时，合并不劣，所以最后答案的形态一定是几段长度减一 $\bmod (k-1)=0$ 且和为 $0$ 的区间拼在一起。

答案为：$\sum\lceil\frac{len-1}{k-1}\rceil=\frac{n}{k-1}-\sum\frac{1}{k-1}$，我们要贪心选取尽量多的合法区间。

再发现 $\lceil\frac{len-1}{k-1}\rceil$ 的上界非常紧，所以我们至多可以这么多次取到环上的所有点，而不被断开。、？？这太抽象了

断环成链，复制一遍。对每个点，找到其后面最小的合法点，倍增跳就行了。

输出方案直接在倍增里找。

做完了。

CF1740H MEX Tree Manipulation

动态 dp。

维护轻儿子的值的集合。

这样相当于每次查询一条重链从链底新加的权值推上来得到的权值，对于每个点维护 $to_{u,vl}$ 表示往 $u$ 的轻儿子集合插入 $vl$ 后的 mex 值。

发现可以合并，线段树搞就行了，这样是 $\mathcal O(n\log ^3 n)$ 的。

发现 $to_{u,vl}$ 的不同值只有两种，这样就是 $\mathcal O(n\log^2n)$ 的。

会了，不写。

CF1380F Strange Addition

秒了。

线性 dp 很好推。

待修就维护矩阵。

不写。

UOJ Round #26 B. 街头庆典

简短的题目：

给定一棵 $n$ 个点的无根树，树上每条边都有相同的长度 $D$。

你可以割掉树上的若干条边，割掉第 $i$ 条边要付出 $w_i$ 的代价。

把一些边割掉后，树变成了若干个连通块。你想使得每个连通块的直径长度之和加上割边付出的代价之和最小，输出这个最小值。

杜吟风观云
岳雄执戟饮
李太白游诗
孔圣临川
杜吟烟云
曹雄登峰
岳山行雨

搬运题解。

https://zhoukangyang.blog.uoj.ac/blog/8846

有启发性的题。

由直径的性质可知，每个联通块包含了距离其直径的中心不超过某个定值的所有点。

分析最优解下，被割掉的边的端点一定是其所在联通块的直径端点，否则联通块直径长度会变大。

于是考虑在以某个点为根下，除了根节点所在联通块，其他联通块一定以其中深度最浅的点为直径端点。

于是我们考虑以直径的端点为根，这下每个联通块都满足以其中深度最浅的点为直径端点，现在直径是直上直下的了。

设计 dp，$f_u$ 表示 $(u,fa_u)$ 的边被割掉时 $u$ 子树内最小代价，设 $s_{u,d}$ 表示 $u$ 子树内割掉所有与 $u$ 距离为 $d$ 的边的代价之和（注意是边深度小的端点与 $u$ 的距离，且割掉后剩下联通块的最小代价也得加上，即要与 $f$ 合并计算）。

直径的中心可能在边的中间，不好记录。

于是记 $g_{u,i}$ 表示 $u$ 所在联通块的中心在 $u$ 子树内，且 $u$ 到联通块深度最浅点的距离为 $i$，最小贡献，注意这里 $u$ 所在的联通块的点可以选取到子树外，因为后面要合并，这样做的好处是可以得知直径的长度和中心，所以 $g_{u,0}$ 等价于 $f$。且我们要在中心算直径的贡献。

考虑转移：

$s$：

• $s_{u,i}=\sum\limits_{v}s_{v,i-1}$，其中 $i\in[1,n]$。
• $s_{u,0}=\sum\limits_{v}f_v+w_{u,v}$。

$g$：

• 中心是 $u$：$g_{u,i}\gets s_{u,i}+2i\times D$，其中 $i\in[0,n]$，意思是先使这是某一直径，再算贡献，这里距离 $u$ 为 $i$ 的祖先即使不存在也不影响，因为我们最终要求的答案是 $g_{rt,0}$。
• 中心在 $u$ 到儿子的边上：
  • $g_{u,i}\gets \min(s_{u,i}-s_{v,i-1}+s_{v,i}+(2i+1)\times D)$，其中 $i\in[1,n]$。
  • $g_{u,0}\gets \min(s_{u,0}-f_{v}-w_{u,v}+s_{v,0}+D)$，此时最浅点为 $u$，但中心在 $(u,v)$ 中间，所以整个联通块只有 $u,v$ 两个点。
• 中心在 $u$ 的儿子的子树内：
  • $g_{u,i}\gets \min(g_{v,i+1} + s_{u,i}-s_{v,i-1})$，其中 $i\in[1,n]$，因为我们要使这条路径为直径，所以得割掉会影响直径的边，就是子树内距离 $u$ 恰为某个定值的边。
  • $g_{u,0}\gets \min(g_{v,1}+s_{u,0}-w_{u,v}-f_{v})$。

反正就是神仙，现在是 $\mathcal O(n^2)$ 的了。

发现 $s$ 的计算可以长链剖分。

现在处理包括根的长链。

情况一：这条长链上的点所在的所有连通块的中心都在长链上。

这等价于每个连通块都存在直径完全在长链上，因为最优解形态下每个联通块的直径都是直上直下的，而中心在长链上，即直径的底端一定是最深的叶子，也在长链上。

形式地，设 $val_{l,r}$ 表示长链上 $[l,r]$ 的点构成了一条直径，大概就是 $\sum\limits_{i=l}^{r}s_{i,\min(i-l,r-i)}^{'}$，其中 $s^{'}$ 表示去除长链影响的贡献。

令 $f_l$ 表示长链上第 $l$ 个点的原 $f$ 值，大概就是 $\min\limits_{r=l}^{t}f_r+val_{l,r}$，其中 $t$ 是长链长度，也就是我们这里并不需要 $g$。

将长链从下往上处理，移动 $l$，更新 $f_r+val_{l,r}$，考虑 $val_{l,r}$ 的变化。

当 $r-i \leq i-l$ 或 $i-l > \text{mx}_i$ 时，$i$ 就不会再发生变化了（$\text{mx}_i$ 表示 $i$ 下挂的短链长度）。

每个 $l$ 移动时，只会将 $l$ 挂的短链对应更新，而对后面的影响是一定的且是一段后缀的 $r$ 的 $val$ 值，根据长链剖分的性质，这部分修改是均摊 $\mathcal O(n)$。

影响并不好快速维护，考虑线段树。

现在长剖维护 $s^{'}$，线段树优化计算 $g$。

现在这个假设下可以做到 $\mathcal O(n\log n)$。

情况二：长链上的点所在的连通块的中心可以在短子树内（或下挂短子树的边中）

（好像情况二是包含情况一的，不管了，下面有用

再考虑上 $g$，发现由于要考虑直径，所以 $g$ 的第二维并不能超过子树最大深度，还是考虑长链剖分维护。

但是当中心在长链上时，综合转移需要数组对位取 $\text{min}$，而且位数是整个子树而非短子树的最大深度，所以此时长链剖分无法保证时间复杂度。

而我们只考虑联通块中心在短链的情况下，位数就是短子树的最大深度了，这下可以进行长链剖分。

于是，将情况一和情况二综合，就会考虑到所有转移，就能得到所有 $f$ 了，但是我们并不能得到 $g$，原因显然。

但是，这种情况只处理了包括根的长链答案，其他链的情况没有算上。

根据第三种转移，发现合并只需要处理链顶的 $g$ 值。

我们发现 $g_{u,i}$ 并不需要考虑 $u$ 之上的点的形态。

为了方便考虑，我们给将长链从上到下从 $0$ 开始标号，并将每条长链从深到浅加上 $t$ 个虚点。

发现，$g_{0,i}$ 的含义与 $f_{-i}$ 的含义是类似的。

可以发现，$g_{0,i}$ 的值也就是直径下端点在长链编号 $\ge i$ 的点的情况加上中心在短链上的情况。

后者前面算过了，前者在扫描线时多考虑一下就行了。

于是我们可以求出所有的 $g_{0,i}$。

这题就以 $\mathcal O(n\log n)$ 的复杂度完成了。

P8290 [省选联考 2022] 填树

钦定最小值 $l$。

方案数就是 $[l,r]-[l+1,r]$，就是容斥掉没有最小值的情况。

现在就是树上的链的乘积，容易想到树形 DP。

发现值域上端点之间的区间每个点的一次函数不变。

对每一段，拉格朗日插值算前缀和就行了。

P3598 Koishi Loves Number Theory

有

$$\gcd(x^a-1,x^b-1)=x^{\gcd(a,b)}-1$$

和

$$\operatorname{lcm}(S)=\prod_{T\subset S}\gcd(T)^{(-1)^{|T|-1}}$$

于是现在就是要求固定长度和 $\gcd$ 下的子集个数。

一种是发现状态数很少，直接开 map 推过去。

另一种是直接莫反。

$10^9$ 下的因子个数最多 $1344$ 个。

$$ans=\prod_d (x^d-1)^{f(d)}\\ f(n)=\sum_{n|d}\mu(\frac{d}{n})g(c(n))\\ g(n)=\sum_{i=1}^{n}(-1)^{i-1}\begin{pmatrix}n \\ i\end{pmatrix}$$

$c(n)$ 是倍数出现次数。

发现 $g(n)=1$。

但是这样中间枚举倍数时复杂度会转到值域上。

考虑另一种莫反，记 $F(x)$ 表示 $\gcd$ 至少为 $x$ 时的转移系数之和。

$$F(x)=\sum (-1)^{|S|+1}[x|k,\forall k\in S]$$

发现 $F$ 就是 $g$，所以 $F(x)=1$。

我们现在要容斥出 $\gcd$ 为 $x$ 的转移系数，那么用 $F(x)$ 减去会出现的 $x|y$ 且 $x\ne y$ 的 $F(y)$ 即可。

做完了。

深层次地，$\mu$ 应该是指的对于值域上的数的容斥，对于值域很大但可能出现的数很少的情况下，可以考虑第二种莫反。

P7011 [CERC2013] Escape

sol 讲的很好。

但是我的 $\mathcal O(n^2)$ 策略怎么寄了，看起来很对。

这里记录一下：

• 首先你维护 1已经走得的联通块
• 每个点记 mn,sum
• sum表示从根的联通块走到u的au和
• mn表示路径上sum的前缀min
• Nw为当前的钱
• 当存在 mn_u+Nw>=0 and Sum_u>=0 时
• 就是能走，且能获得钱
• 就一直走
• 每走一次根的联通块至少多一个点
• 预处理先把1-t的链拉出来
• 如果走的时候搞到链上了，就记录这条链扩展到的最深的点
• 如果一直走还没有走到t
• 就从强制把最深的这个点往下走一层
• 再一直走
• 每次走到一个点只会影响他子树内的sum和 min
• sum修改其实是可以优化的，但是前缀 min 直接修改会产生问题，所以 Onlogn 并无正确性

给 $t$ 建个 $a=+\infty$ 的儿子。

设 $f_{u,i}$ 表示以 $i$ 的血量进入子树 $u$ 中最多可以获得 $f_{u,i}$ 的血量。

发现 $f$ 是一层一层地变化。

做类似差分的变化。

设 $g_u$ 为若干二元组 $(x,y)$ 的集合，表示如果当前血量 $\ge x$，那么额外加上 $y$，数量只有子树大小。

那么求 $f_{u,i}$ 就是不断取出 $x$ 最小的二元组，算和。

儿子的合并就是将所有儿子的 $g$ 合并。

考虑加入 $a_u$：

• 若 $a_u>0$，那么在 $g_u$ 中加入 $(0,a_u)$ 即可；
• 否则，将一段前缀删除，并添加一个二元组，具体细节简单推。

启发式合并做到双 $\log$。

P7115 [NOIP2020] 移球游戏

喵了个喵早就理解了，不写。

分析，这题的空栈始终存在，不需要对具体操作序列进行考虑。

现在 $n=2$，记录一下，较小的大样例十分有用，因为使用 std 跑的。

策略，设空栈 $z$，我们要将第一根柱子 $x$ 和第二根柱子 $y$ 上的 $0$ 和 $1$ 分离开，假设是 $x$ 上全是 $1$，$y$ 上全是 $0$，设原来 $x$ 上有 $a$ 个 $1$：

1. 将 $y$ 的 $a$ 个移到 $z$；
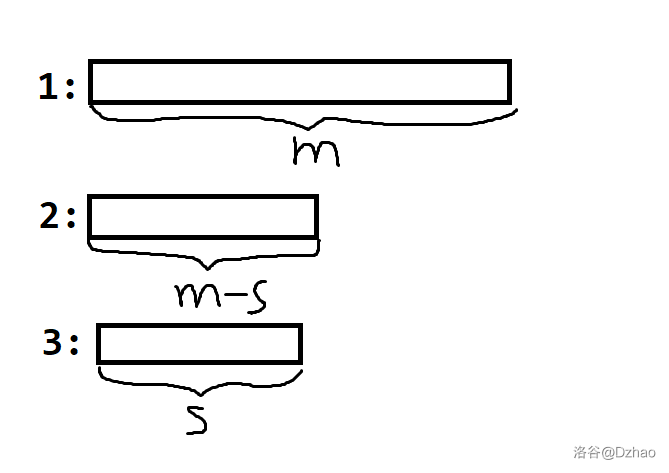
2. 不断弹出 $x$，若是 $1$ 放到 $y$，否则放到 $0$，现在 $x$ 空了；
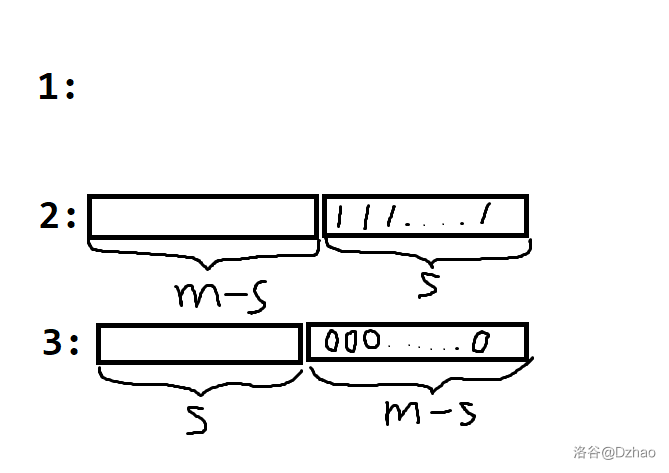
3. 将 $y$ 上的 $a$ 个 $1$ 放到 $x$，再将 $z$ 上的 $m-a$ 个 $0$ 放到 $x$，将 $y$ 中剩下的全部塞到 $z$，现在 $y$ 空了；
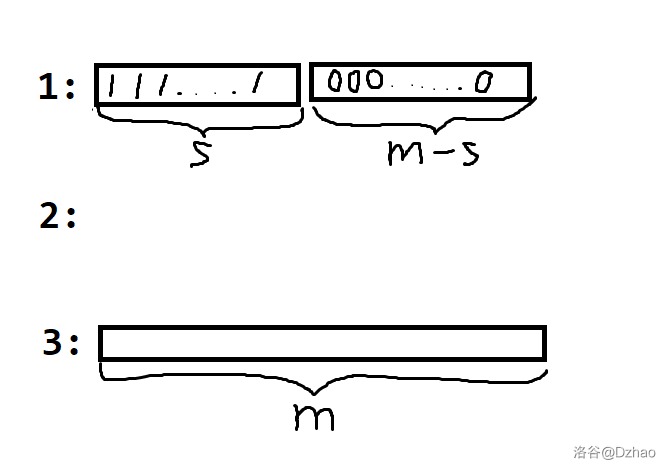
4. 将 $x$ 上的 $m-a$ 个 $0$ 放到 $y$；
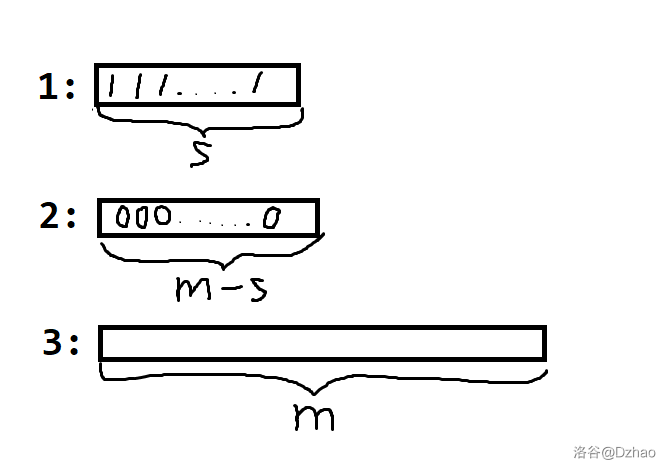
5. 不断弹出 $z$，若是 $1$ 放到 $x$，否则放到 $y$。

保存题解图片。

操作次数为 $5m-a$。

考虑多种颜色怎么做。

我们要尽可能将多种颜色转化为两种颜色去求解。

设阈值 $x$，将 $\le x$ 的设成 $1$，$>x$ 的设成 $0$。

将 $[l,mid]$ 和 $[mid+1,r]$ 两两匹配，若两个栈中 $\le x$ 的个数 $\ge m$，就将前一个栈放满同样的数，否则将后一个栈放满同样的数，因为球的总数一定，所以最后一定能全部放满。

操作数。

$$T(n)=2T(n/2)+5mn\\ T(n)=5mn\log n$$

https://www.luogu.com.cn/record/133045914

CF1582G

有点神奇。

CSP 的是每种字符合起来考虑。

这里发现这东西合起来不具有单调性。

质因子是独立的。

考虑对于质因子分别考虑，乘号就是加，除号就是减。

对于单独的一个质因子，一个区间合法要区间所有前缀和 $\ge 0$。

维护前缀和，对于 $pre_i$ 找到其后第一个 $j$ 满足 $pre_j<pre_i$，则右端点在 $[i,j-1]$ 的区间都合法。

我们要保证复杂度，只对出现过这个质因子的点进行考虑，因为其他点的 $pre$ 值分段相同。

单调栈处理就行了。

这下有 $\mathcal O(n\log n)$ 次区间取 min，经典并查集。

CF1628D2 Game on Sum (Hard Version)

顺着 dp 不方便转移，因为两人绝顶聪明使得当前决策仅基于接下来的决策。

重点！！！

CF1548E 地皮 (dp)

对联通块找代表元，按照 $(a_i+b_j,i,j)$ 排序下最小的点。

我们只需统计代表元个数即可。

令 $pre1_i$ 表示 $i$ 之前的 $a_j\le a_i$ 的最大的 $j$，$suf1_i$ 表示 $i$ 之后的 $a_j<a_i$ 的最小的 $j$，列同理。

那么一个点是代表元当且仅当这个点不能走到 $pre1_i$ 行和 $suf1_i$ 行，还有列。

可以发现，$(i,j)$ 走到 $pre1_i$ 行当且仅当 $(i,j)$ 能走到 $(pre1_i,j)$，其他三个方向同理。

购买饮料 (buy)

相当于当 $n>ax$ 时，花费 $ax-b$ 获得一次机会。

多边形(polygon)

相邻点的颜色必不同。

如果存在一个颜色只出现了一次，那么直接把这个点和所有其他点相连即可。

否则会出现一段一段交替的，所以一定会存在相邻三个点颜色两两不同，直接划分。

所以我们就是找这些最近的三点对，链表维护即可。

二分图最大权匹配(match)

现在对曼哈顿距离的绝对值进行讨论。

拆成四个方向。

而我们的费用流只会选取和最大的流，即流过曼哈顿距离。

源 - 左侧点 - 颜色 - 右侧点 - 汇。

发现这个模型很好模拟费用流。

退流路径，只会是源 - 左侧 - 颜色 - 左侧/右侧 - 颜色 - … 颜色 - 右侧 - 汇，即在颜色处左右反复横跳，最后到汇点。

而因为退流路径不会经过同一个点，又因为只有四种颜色，所以本质不同的退流路径只有大约 $64$ 种，全部维护一下即可。

分别开三种可删堆，分别表示左侧到颜色、颜色到左侧/右侧再到另一个颜色、颜色到右侧目前可以走的边。

随便维护就做完了。

飞毯(carpet)

啊？又是冷门数列科技题。

预习 欧拉路径与 de Bruijn 序列。

猜测对于长度为 $k$ 的子串，其在最优解中出现为 $\min(2^k,n-k+1)$。

则猜测最优解为 $\sum\limits_{i=1}^{n}\min(2^k,n-k+1)$，分别表示全部出现和互不相同两种意思。

显然如果长度为 $k$ 的串均出现，那么 $\le k$ 的均满足；如果长度为 $k+1$ 的区间互不相同，那么长度 $>k$ 的均满足。

则 $k$ 需满足的条件为：

$$2^k\le n-k+1\\ 2^{k+1}>n-k+1$$

即 $2^k+k-1\le n<2^{k+1}+k-1$。

我们构造一个 de Bruijn 序列，建点在 $[0,2^k)$ 的有向图，$x$ 连边 $2x \bmod 2^k$ 和 $(2x+1)\bmod 2^k$。

有性质：在 $2^{k-1}$ 的图上的欧拉回路，就是 $2^k$ 的图上的哈密顿回路。

当 $n=2^k+k-1$ 时，这个图的哈密顿回路就是解了。

当 $n>2^k+k-1$ 时。

为了保留长度 $\le k$ 的串全部出现的特性，我们首先构造一个 $2^k+k-1$ 的答案，再将其放在 $2^{k+1}$ 的 de Bruijn 图上考虑。

此时对于 $x\in[0,2^k)$，$x,x+2^k$ 中一定有一个点被考虑到了，可以通过互不相同和后 $k$ 位不同反证。

对于 $x\in[0,2^k)$，$x$ 和 $x+2^k$ 的出边相同，而其中只有一个点被考虑了，所以剩下点的出边也确定了。

整个图形成了一个长为 $2^k$ 的大环加上若干小环。

我们找到一个 $x$ 使得 $x,x+2^k$ 不在同一个圈，那么这两个圈一定有一个是大圈，合并起来，知道大圈的长度 $>n-k$，就跑一边这个圈输出答案即可。

旅行(tour)

竟然卡双 $\log$ 做法/ng

对于树上数联通块，考虑点减边容斥，边联通块也是一样。

计算被联通块包含的点的数量，以及被联通块包含边的数量。

对于环上所有边同一颜色时，答案加一。

对每个点开个桶就很好维护了。

点餐(order)

首先按 $b$ 排序。

固定最大的 $b$，然后就相当于取前缀前 $k-1$ 小的 $a$，主席树维护。

记 $w_{k,x}$ 表示长度为 $k$，$b$ 取第 $x$ 位时的答案。

令 $f(k)$ 表示使 $k$ 取到最优解的 $x$。

对于决策 $x,y$，$x<y$，若 $w(k,x)\ge w(k,y)$，则必定满足 $\forall k'\in[k,n],w(k',x)\ge w(k',y)$。

由此得证决策单调性。

经典分治了。

无穷括号序列(seq)

QOJ7106

https://sua.ac/wiki/2018-icpc-qingdao-online/e/#_2

const int _ = 2e5 + 5;

int n, a[_], lg[_], m;

int st[21][_];

char str[_];

bool Med;
signed main() {
	// Mry;
	auto solve = [&]() {
		scanf("%s", str + 1);
		n = strlen(str + 1);
		int q = ri();
		auto init = [&]() {
			m = 0;
			F(i, 0, n - 1) if(str[i + 1] == '(') st[0][m++] = i;
			F(i, m, m + m - 1) st[0][i] = st[0][i - m] + n;
			F(i, 0, m + m - 1) st[0][i] -= i + i;
			F(j, 1, 20) F(i, 0, (m + m - 1) - (1 << j) + 1) {
				st[j][i] = min(st[j - 1][i], st[j - 1][i + (1 << (j - 1))]);
			}
		}; init();
		auto qryF = [&](ll k, ll i) -> ll {
			ll L, R;
			if(n - 2 * m >= 0) { // [i, i + m)
				L = i;
				R = min(i + k, L + m - 1);
			} else { // (i + k - m, i + k]
				R = i + k;
				L = max(i, R - m + 1);
			}
			// f(k, i) = min_{i\le j \le i + k} (f(0,j) + k - 2j + 2i)
			// F(j) = f(0, j) - 2j
			// F(j + t) = F(j mod m + t) + (n - 2m) * \lfloor j / m \rfloor
			ll dk = (L >= 0 ? L / m : (L + 1) / m - 1);
			// [i, i + k] \to [i mod m, i mod m + k]
			int mod = (L % m + m) % m, t = lg[R - L + 1];
			return min(st[t][mod], st[t][mod + R - L + 1 - (1 << t)]) + dk * n - 2ll * dk * m + k + 2 * i;
		};
		auto qryG = [&](ll k, ll p) -> ll {
			ll L = -3e9, R = 3e9, mid, res;
			while(L <= R) {
				mid = (L + R) >> 1;
				if(qryF(k, mid) <= p) res = mid, L = mid + 1;
				else R = mid - 1;
			}
			return res;
		};
		int k, l, r;
		while(q--) {
			k = ri(), l = ri(), r = ri();
			if(!m) printf("0\n");
			else {
				printf("%lld\n", qryG(k, r) - qryG(k, l - 1));
			}
		}
	};
	F(i, 2, _ - 4) lg[i] = lg[i >> 1] + 1;
	int T = ri();
	while(T--) solve();
	// Try;
	return 0;
}

CF1895F Fancy Arrays 题解

考虑到 $x\le 40$，肯定是要从这上面考虑的。

我们把存在性容斥掉，答案为总情况数减去所有数在 $[0,x)$ 的情况数再减去所有数在 $(x+k-1,+\infty)$ 的情况。

考虑第一部分和第三部分一起看。

绝对值转成差分序列 $b$，那么 $b_i\in[-k,k]$，即只有 $2k+1$ 种取值。

而第一部分减去第三部分等价于原序列的最小值在 $[0,x+k-1]$。

则这种情况的方案数为 $(x+k)\times (2k+1)^{n-1}$。

剩下的部分就显而易见了。

设计 dp，设 $f_{i,j}$ 表示所有数在 $[0,x)$ 且相邻差 $\le k$ 的序列，第 $i$ 位为 $j$ 的方案数。

转移方式固定，矩阵乘法加速转移即可。

时间复杂度 $\mathcal O(x^3\log n)$。

种树（plant）

同一时刻区间不相交

我们考虑一个点种树的期望，就是次数除以总方案数。

设有 $p1$ 个一类区间包含它，$p2$ 个二类区间包含它。

那么它有树必须得最后一个生效的区间的个一类区间，且考虑时间在它前面的区间任取。

那么合法方案数就是：

$$p(p+q-1)!\sum_{i=0}^{p+q-1}2^i=p(2^{p+q}-1)(p+q-1)!$$

总的就是：

$$\frac{p(2^{p+q}-1)}{(p+q)2^{p+q}}$$

汪了个汪（wow）

考虑查询操作，在修改操作下，数的相对位置不变，可转化为求初始区间第 $k$ 大后进行单点查询。

发现这个修改操作在 $\log V$ 次之后初始值的影响微乎其微。

容易发现最后只剩下不超过两种数，且相差一。

容易维护。

赛比（hctam）

矩阵是 $(2n)\times (2m)$ 的，分成 $n\times m$ 个 $2\times 2$ 的矩阵，记为大矩阵。

在最优解下，每个大矩阵有且仅有一个障碍物，且同一行的大矩阵前缀的障碍物在右，后缀的障碍物在左，同一列的大矩阵前缀的障碍物在下，后缀的障碍物在上。

设计 dp，设 $f_{i,j,s}$ 表示考虑前 $i$ 列，第 $i$ 列的前 $j$ 个大矩阵障碍物在下方，且 $s$ 集合中的行对应的大矩阵障碍物在右方，考虑从上一列转移过来的集合 $s'$，首先要满足 $s\in s'$。

但是还有两种不合法的情况。

$$\texttt{.X..}\\ \texttt{...X}\\ \texttt{X...}\\ \texttt{..X.}\\ $$

右风车，描述一下。

设这两列分别为第 $i-1$ 列和第 $i$ 列，下面一行为第 $p$ 行，第 $i-1$ 列前 $k$ 个在下，第 $i$ 列前 $j$ 个在下，第 $i$ 列的行集合为 $s$，第 $i-1$ 列的行集合为 $s’$。

对于第 $i-1$ 列，有 $k\ge p,p-1\notin s',p\in s'$。

对于第 $i$ 列，有 $j<p-1,p-1\notin s, p\in s$。

为了去除此条件，发现第 $i-1$ 列只有上方的点能动，满足 $p-1\in s'$ 即可。

$$\texttt{..X.}\\ \texttt{X...}\\ \texttt{...X}\\ \texttt{.X..}\\ $$

左凤车，变量同上。

对于第 $i-1$ 列，有 $k<p-1,p-1\in s',p\notin s'$。

对于第 $i$ 列，有 $j\ge p, p-1\in s, p\notin s$。

此时只需满足 $p\in s'$ 即可。

这两种情况都很好讨论，我们预处理 $to_{s,j,k}$ 表示 $s'$ 即可。

时间复杂度 $\mathcal O(2^n n^3+mn^22^n)$。

建造食堂（canteen）

初始想法肯定是构造 $k=0$ 的矩阵。

1				25
21	2
	22	3
		23	4
			24	5

然后 $k=1$，就直接交换行列。

$k=2$，就根据根据初始矩阵两个数是否在同一集合和最后要求两个数是否在同一集合进行合并或分拆。

合并，只需将两个数交换到相邻行，然后进行合并，分讨最小次小最大次大是否交换即可。

分拆同理。

发现很多情况跑不出来。

本质原因是矩阵不优，我们考虑手动构造矩阵进行合并和分拆。

观察原矩阵的形式，发现只需要考虑两个数都在 $[1,n]\cup[n(n-1)+1,n^2]$ 的情况。

此时我们只有查询 $i,i+n(n-1)$ 或 $1,n^2$ 或 $n,n^2$ 是才需要分拆，放到后面考虑。

考虑合并，无非就是将手动构造将两个数放到同行或同列。

构造矩阵很烦，我们打表。

link

弄出一堆表，找规律就行了。

补充题解没有的几张表。

$b_{i,i}=i+[i\ge x],b_{i+1,i}=n(n-1)+i+[i\ge x-1],b_{1,n}=n(n-1)+x-1,b_{y,n}=x$

$b_{i,i}=i+[i\ge x],b_{i+1,i}=n(n-1)+i+1,b_{1,n-1}=n(n-1)+1,b_{1,n}=x$

$b_{i,i}=i+[i\ge x](i\le n-1),b_{i+1,i}=n(n-1)+i+[i\ge x-1],b_{1,n-1}=n(n-1),b_{1,n}=x,b_{n,n}=n(n-1)+x-1,a_{n,1}=n+1$

分拆的情况也考虑在合并的表内了。

把每个表都带到上面算法里就一定能跑出解。

mspaint

有点神，要好好总结。

在只考虑第一代价的时候，将区间中的数全部变成区间中任意数与全部变成区间左端点或右端点无本质区别，有简单的 $\mathcal O(n^3)$。

再考虑第二代价，有简单的 $\mathcal O(n^4)$。

第一代价仍是非常强的限制，它要求最少操作次数，因此每一次修改都应该使得修改后状态的最小操作数减少 $1$，由此我们得到两个结论：

1. 选择的区间必须是极长连续段；
2. 若某次布置魔法阵将区间 $[l,r]$ 最终转化为了 $y$ 那么在现在或将来的某一刻一定有区间左侧或右侧的数等于 $y$。

考虑第二条性质，不妨直接把这次操作延后到左侧或右侧的数等于 $y$，那么我们现在的操作就是将区间变为左侧或右侧的数。

设 $f_{l,r}$ 表示区间左右端点不变，中间的一段前缀变为 $s_l$，剩余变为 $s_r$ 的最小代价。

转移的时候枚举中枢点 $k$，$f_{l,r}=\min\limits_{k=l}^r(f_{l,k}+f_{k,r}+\min(\operatorname{dis}(s_k,s_l),\operatorname{dis}(s_k,s_r)))$。

最后枚举 $s$ 最终的值统计答案即可。

tourist

先随便并查集找一下初始的跳跃路径以及每条路径新走过的点的集合。

对于询问，从根开始往下搜，如果某条路径的整个集合都出现过，就要删去这条路径，具体就用链表模拟就行了。

segment

bitset。

$v_i=0$ 时，记录第 $i$ 维坐标 $\le j$ 的点集，询问简单，现在是 $\mathcal O(\frac{nmq}{w})$。

再考虑带上权值，我们找到要覆盖的点集后逐位模拟二进制减法，时间复杂度 $\mathcal O(\frac{nq(\log v+m)}{w})$。

考虑到高位的 $V$ 在减法下变化量很少，设阈值 $k$，对前 $k$ 位模拟二进制减法，后面的位置暴力找出并修改，可以做到 $\mathcal O(\frac{nq(k+m)}{w}+\frac{nv}{2^k})$，要算上 _Find_next 的小常数。

game

首先，使用 $(d+1)\lfloor\log_2(n)\rfloor$ 次询问的操作是平凡的，具体而言就是暴力二分，每次询问就询问 $(d+1)$ 次得到真正的答案。

但这样无疑是很浪费的，我们完全可以把那些用来充次数的询问更加充分地利用。

先从简单情况入手。考虑 $d=1$：

你的第一次询问必然是没有结果的。但是你也不能浪费第二次询问，考虑随便把第二次询问放在第一次询问的左边或右边。假设为左边。

此时如果第一次询问的结果为 $-1$，那么你的第二次询问算是浪费掉了；否则若为 $1$，那么第二次询问并没有浪费。

发现两种情形都是可递归处理的：若为前者情况，那么来到了「当前区间没有询问过」的情形；若为后者，那么就是「当前区间询问过一次，但还没有返回结果」的情形，与询问完第一次询问后的情形相似。

于是可以设一个递推式：设 $f_i$ 表示 $i$ 次询问能够确定的最大的范围，那么有 $f_i=f_{i-1}+f_{i-2}+1$。

具体地，对于一个 $f_i$ 长度的区间，先询问 $f_{i-1}+1$，在询问 $f_{i-1}$ 的最优决策点。若第一次询问的结果为 $-1$，那么按照 $f_{i-2}$ 的最优决策处理右半部分；否则继续按照 $f_{i-1}$ 的最优决策处理左半部分。

接下来的工作是容易的。当 $d>1$ 时，假设在第一次询问后在左半部分询问 $a$ 次，在右半部分询问 $b$ 次，那么 $f_i=f_{i-a-1}+f_{i-b-1}+1$。容易发现当 $a=0,b=d$ 时最优，此时 $f_i=f_{i-1}+f_{i-d-1}+1$，需要的询问次数为 $\min\limits_{f_i\ge n}i$，可以通过此题。