随着2012年AlexNet赢得了ImageNet挑战赛的冠军后,深度学习技术在各个领域都发挥着重要的作用,极大地提升了许多任务的SOTA。2014年,DeepFace首次在著名的非受限环境人脸数据集——LFW上取得了与人类相媲美的准确率(DeepFace: 97.35% vs. Human: 97.53%)。因此,本文主要关注深度学习技术在人脸识别领域的应用与发展。
概念和术语
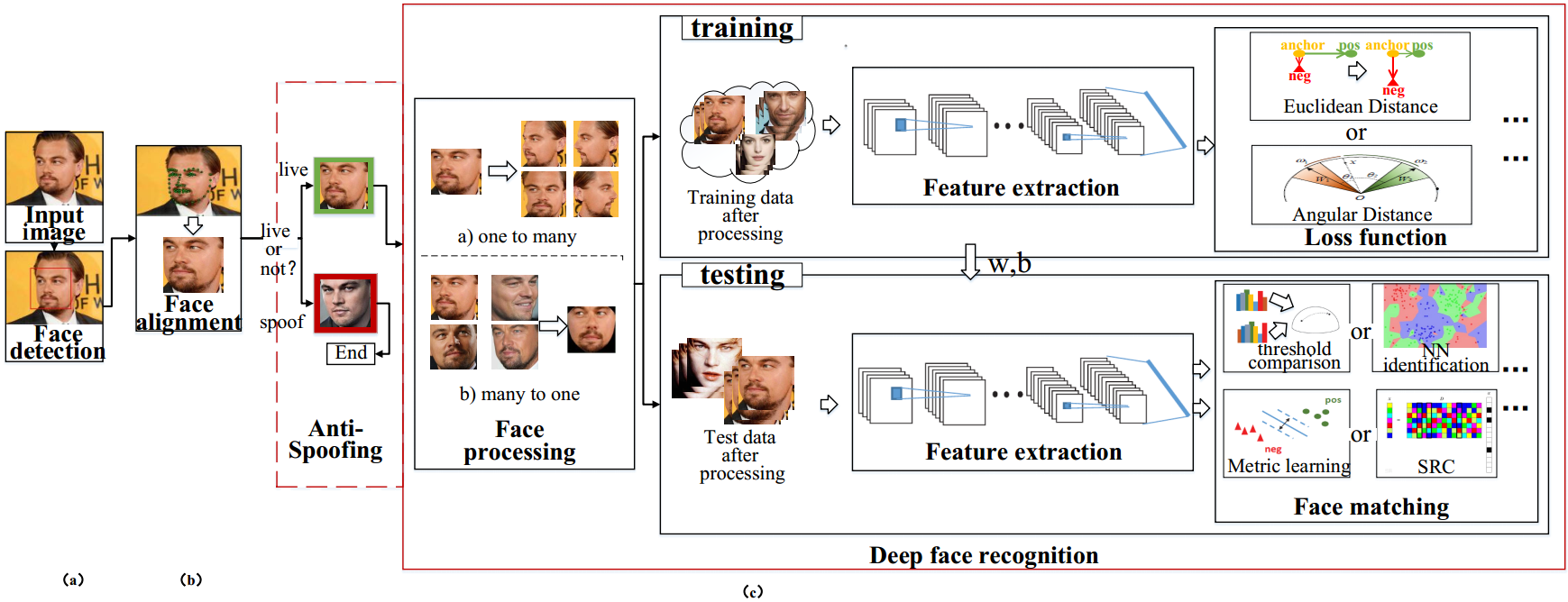
人脸系统一般包括三个部分:
-
人脸检测(face detection):对于一幅图像,检测其中人脸的位置;
-
人脸对齐(face alignment):根据人脸关键点,将人脸对齐到一个典型的角度;
-
人脸识别(face recognition):包括人脸处理、人脸表示和人脸匹配部分。
人脸识别任务主要包括:
网络结构
主流结构
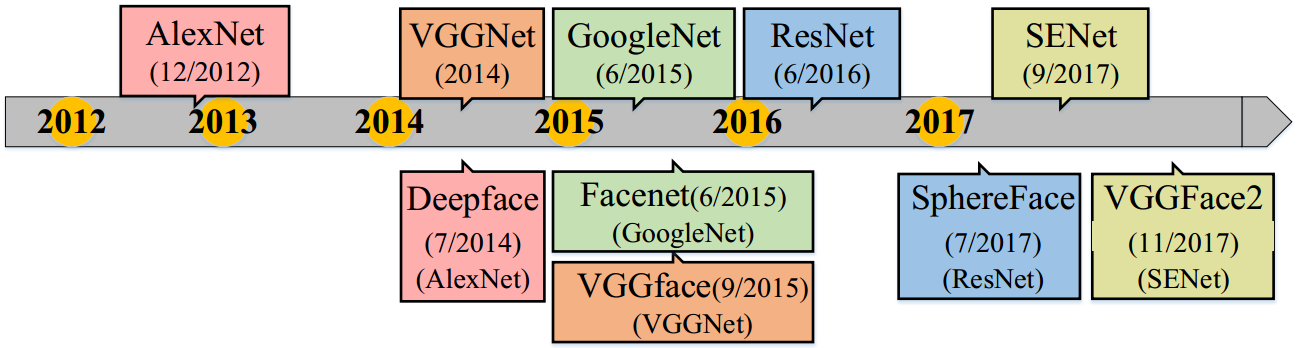
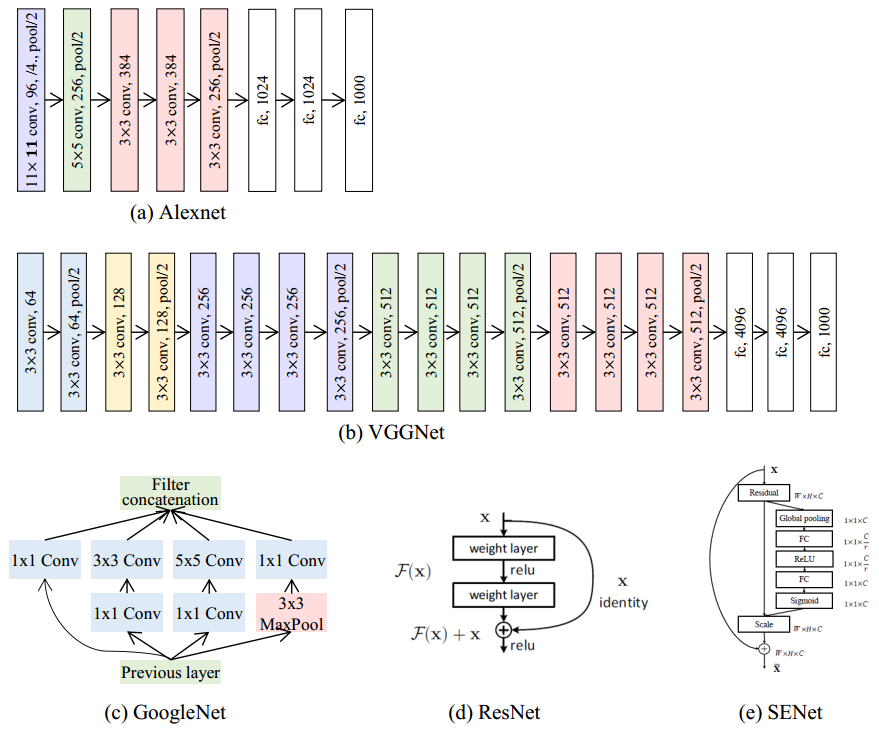
在人脸识别问题中,主流的网络结构基本上都借鉴于物体分类问题,一直从AlexNet到SENet。
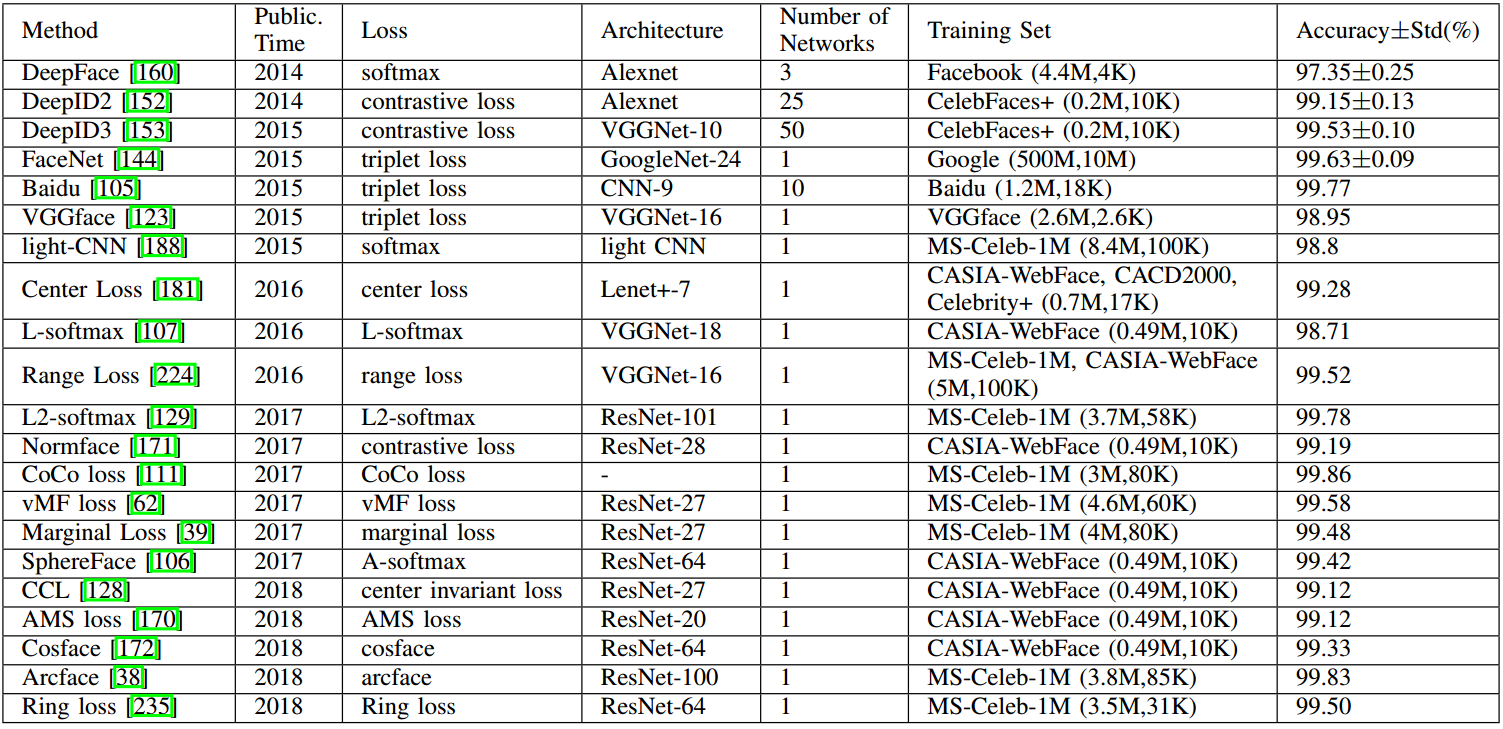
在2014年,DeepFace首次使用九层的卷积神经网络,经过3D人脸对齐处理,在LFW上达到了97.35%的准确率。在2015年,FaceNet在一个很大的私人数据集上训练GoogLeNet,采用triplet loss,得到99.63%的准确率。同年,VGGface从互联网中收集了一个大的数据集,并在其上训练VGGNet,得到了98.95%的准确率。在2017年,SphereFace使用64层的ResNet结构,采用angular softmax(A-softmax)loss,得到99.42%的准确率。在2017年末,VGGFace2作为一个新人脸的数据集被引入,同时使用SENet进行训练,在IJB-A和IJB-B上都取得SOTA。
-
AlexNet:AlexNet包括五个卷积层和三个全连接层,并且集成了如ReLU、dropout、数据增强等技术;
-
VGGNet:使用3×3卷积核,且每经过2×2的池化后特征图数量加倍,网络深度为16-19层;
-
GoogLeNet:提出了inception module,对不同尺度的特征图进行混合;
-
ResNet:通过学习残差表示,使得训练更深网络成为可能;
-
SENet:提出了Squeeze-and-Excitation操作,通过显式建模channel之间的相互依赖性,自适应地重新校准channel间的特征响应。
特殊结构
-
Light CNN
-
bilinear CNN
-
...
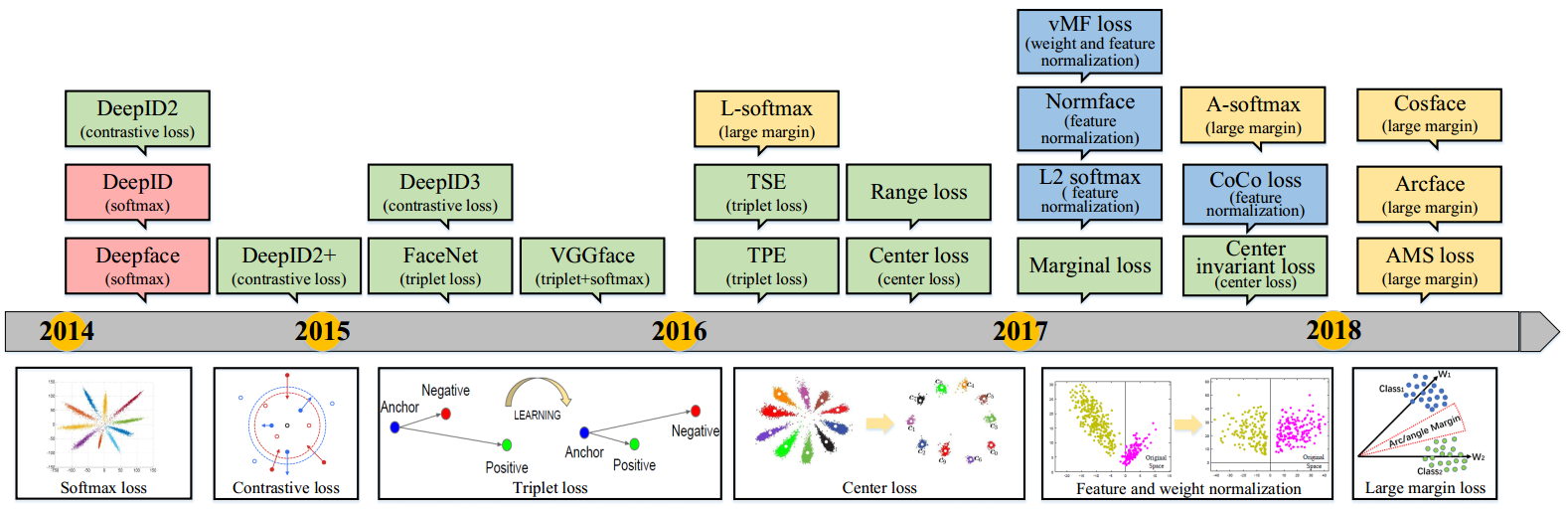
损失函数
在一开始,人们使用和物体分类同样的基于交叉熵的softmax loss,后来发现其不适用于人脸特征的学习,于是开始探索更具有判别性的loss。
基于欧几里德距离
contrastive loss
相关文献:
- 《Deep learning face representation by joint identification-verification》
- 《Deepid3: Face recognition with very deep neural networks》
DeepID系列使用的loss。
\[\operatorname { Verif } \left( f _ { i } , f _ { j } , y _ { i j } , \theta _ { v e } \right) = \left\{ \begin{array} { l l } { \frac { 1 } { 2 } \left\| f _ { i } - f _ { j } \right\| _ { 2 } ^ { 2 } } & { \text { if } y _ { i j } = 1 } \\ { \frac { 1 } { 2 } \max \left( 0 , m - \left\| f _ { i } - f _ { j } \right\| _ { 2 } \right) ^ { 2 } } & { \text { if } y _ { i j } = - 1 } \end{array} \right.
\]
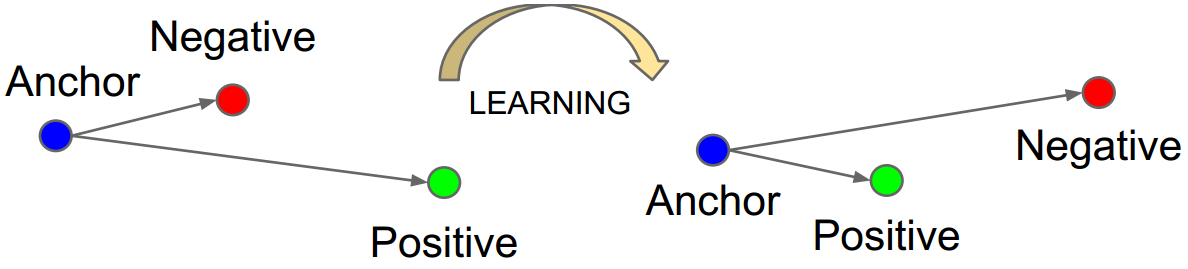
triplet loss
相关文献:
- 《Facenet: A unified embedding for face recognition and clustering》
\[\mathcal{L} = \sum _ { i } ^ { N } \left[ \left\| f \left( x _ { i } ^ { a } \right) - f \left( x _ { i } ^ { p } \right) \right\| _ { 2 } ^ { 2 } - \left\| f \left( x _ { i } ^ { a } \right) - f \left( x _ { i } ^ { n } \right) \right\| _ { 2 } ^ { 2 } + \alpha \right] _ { + }
\]
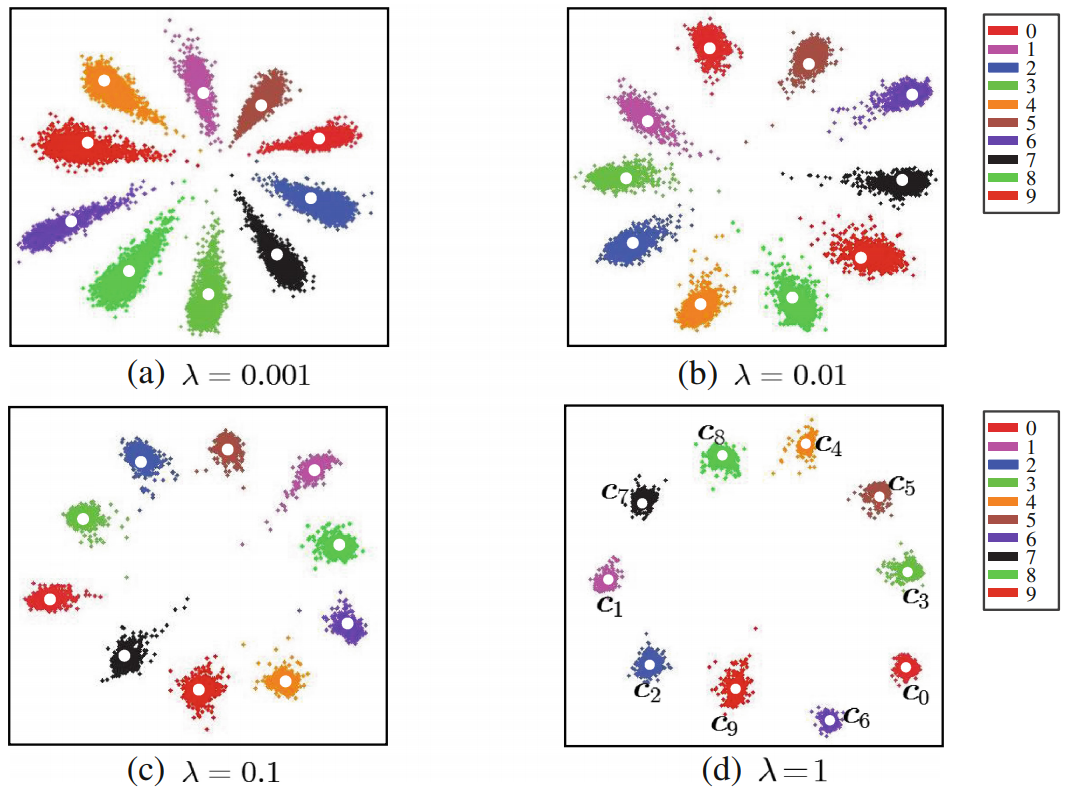
center loss
相关文献:
- 《A Discriminative Feature Learning Approach for Deep Face Recognition》
\[\begin{aligned} \mathcal { L } & = \mathcal { L } _ { S } + \lambda \mathcal { L } _ { C } \\ & = - \sum _ { i = 1 } ^ { m } \log \frac { e ^ { W _ { y _ { i } } ^ { T } \boldsymbol { x } _ { i } + b _ { y _ { i } } } } { \sum _ { j = 1 } ^ { n } e ^ { W _ { j } ^ { T } \boldsymbol { x } _ { i } + b _ { j } } } + \frac { \lambda } { 2 } \sum _ { i = 1 } ^ { m } \left\| \boldsymbol { x } _ { i } - \boldsymbol { c } _ { y _ { i } } \right\| _ { 2 } ^ { 2 } \end{aligned}
\]
range loss
相关文献:
- 《Range loss for deep face recognition with long-tail》
\[\mathcal { L } _ { R } = \alpha \mathcal { L } _ { R _ { intra } } + \beta \mathcal { L } _ { R _ { inter } }
\]
\[\mathcal { L } _ { R _ { i n t r a } } = \sum _ { i \subseteq I } \mathcal { L } _ { R _ { i n t r a }}^ { i } = \sum _ { i \subseteq I } \frac { k } { \sum _ { j = 1 } ^ { k } \frac { 1 } { \mathcal { D } _ { j } } }
\]
\[\begin{aligned} \mathcal { L } _ { R _ { \text {inter} } } & = \max \left( m - \mathcal { D } _ { C e n t e r } , 0 \right) \\ & = \max \left( m - \left\| \overline { x } _ { \mathcal { Q } } - \overline { x } _ { \mathcal { R } } \right\| _ { 2 } ^ { 2 } , 0 \right) \end{aligned}
\]
\[\mathcal { L } = \mathcal { L } _ { M } + \lambda \mathcal { L } _ { R } = - \sum _ { i = 1 } ^ { M } \log \frac { e ^ { W _ { y _ { i } } ^ { T } x _ { i } + b _ { v _ { i } } } } { \sum _ { j = 1 } ^ { n } e ^ { W _ { j } ^ { T } x _ { i } + b _ { j } } } + \lambda \mathcal { L } _ { R }
\]
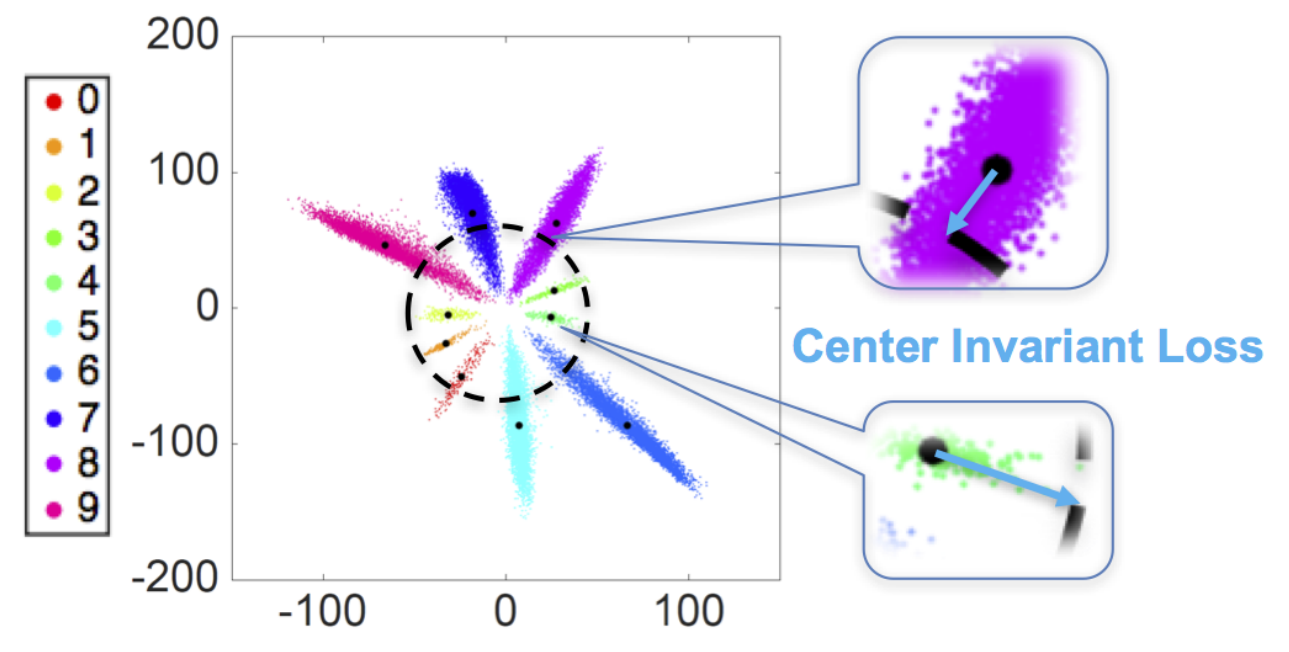
center-invariant loss
相关文献:
- 《Deep face recognition with center invariant loss》
\[\begin{aligned} L = & L _ { s } + \gamma L _ { I } + \lambda L _ { c } \\ = & - \log \left( \frac { e ^ { \mathbf { w } _ { y } ^ { T } \mathbf { x } _ { i } + b _ { y } } } { \sum _ { j = 1 } ^ { m } e ^ { \mathbf { w } _ { j } ^ { T } \mathbf { x } _ { i } + b _ { j } } } \right) + \frac { \gamma } { 4 } \left( \left\| \mathbf { c } _ { y } \right\| _ { 2 } ^ { 2 } - \frac { 1 } { m } \sum _ { k = 1 } ^ { m } \left\| \mathbf { c } _ { k } \right\| _ { 2 } ^ { 2 } \right) ^ { 2 } \\ & + \frac { \lambda } { 2 } \left\| \mathbf { x } _ { i } - \mathbf { c } _ { y } \right\| ^ { 2 } \end{aligned}
\]
基于角度/余弦间隔
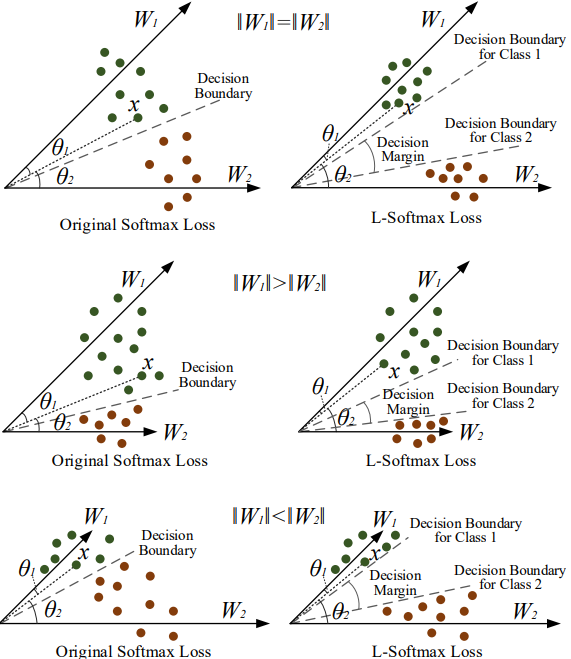
L-Softmax loss
相关文献:
- 《Large-margin softmax loss for convolutional neural networks》
\[L _ { i } = - \log \left( \frac { e ^ { \left\| \boldsymbol { W } _ { y _ { i } } \right\| \left\| \boldsymbol { x } _ { i } \right\| \psi \left( \theta _ { y _ { i } } \right) } } { e ^ { \left\| \boldsymbol { W } _ { y _ { i } } \right\| \boldsymbol { w } \left( \theta _ { \boldsymbol { y } _ { i } } \right) } + \sum _ { j \neq y _ { i } } e ^ { \left\| \boldsymbol { W } _ { j } \right\| \left\| \boldsymbol { x } _ { i } \right\| \cos \left( \theta _ { j } \right) } } \right)
\]
\[\psi ( \theta ) = ( - 1 ) ^ { k } \cos ( m \theta ) - 2 k , \quad \theta \in \left[ \frac { k \pi } { m } , \frac { ( k + 1 ) \pi } { m } \right]
\]
\[f _ { y _ { i } } = \frac { \lambda \left\| \boldsymbol { W } _ { y _ { i } } \right\| \left\| \boldsymbol { x } _ { i } \right\| \cos \left( \theta _ { y _ { i } } \right) + \left\| \boldsymbol { W } _ { y _ { i } } \right\| \left\| \boldsymbol { x } _ { i } \right\| \psi \left( \theta _ { \boldsymbol { y } _ { i } } \right) } { 1 + \lambda }
\]
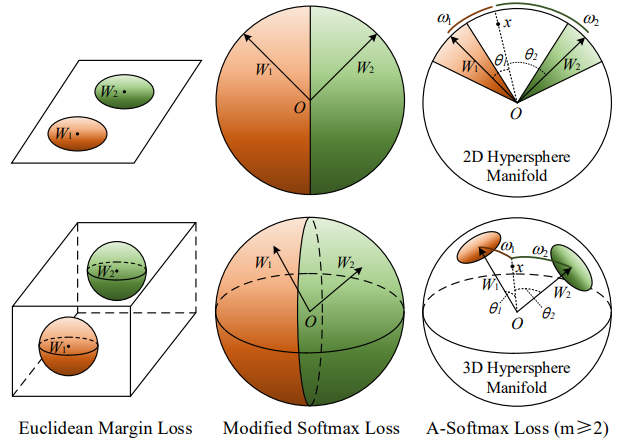
A-Softmax loss
相关文献:
- 《Sphereface: Deep hypersphere embedding for face recognition》
\[L _ { \mathrm { ang } } = \frac { 1 } { N } \sum _ { i } - \log \left( \frac { e ^ { \left\| \boldsymbol { x } _ { i } \right\| \psi \left( \theta _ { y _ { i } , i } \right) } } { e ^ { \left\| \boldsymbol { x } _ { i } \right\| \psi \left( \theta _ { y _ { i } } , i \right) } + \sum _ { j \neq y _ { i } } e ^ { \left\| \boldsymbol { x } _ { i } \right\| \cos \left( \theta _ { j , i } \right) } } \right)
\]
\[\psi \left( \theta _ { y _ { i } , i } \right) = ( - 1 ) ^ { k } \cos \left( m \theta _ { y _ { i } , i } \right) - 2 k
\]
\[\theta _ { y _ { i } , i } \in \left[ \frac { k \pi } { m } , \frac { ( k + 1 ) \pi } { m } \right] \text { and } k \in [ 0 , m - 1 ]
\]
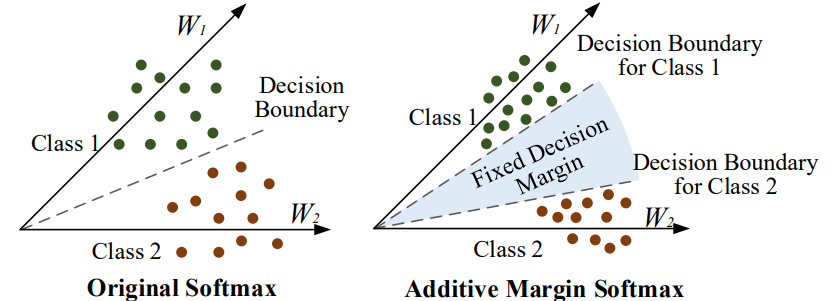
AM-Softmax loss
相关文献:
- 《Additive margin softmax for face verification》
\[\begin{aligned} \mathcal { L } _ { A M S } & = - \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \log \frac { e ^ { s \cdot \left( \cos \theta _ { y _ { i } } - m \right) } } { e ^ { s \cdot \left( \cos \theta _ { y _ { i } } - m \right) } + \sum _ { j = 1 , j \neq y _ { i } } ^ { c } e ^ { s \cdot c o s \theta _ { j } } } \\ & = - \frac { 1 } { n } \sum _ { i = 1 } ^ { n } \log \frac { e ^ { s \cdot \left( W _ { y _ { i } } ^ { T } f _ { i } - m \right) } } { e ^ { s \cdot \left( W _ { y _ { i } } ^ { T } \boldsymbol { f } _ { i } - m \right) } + \sum _ { j = 1 , j \neq y _ { i } } ^ { c } e ^ { S W _ { j } ^ { T } \boldsymbol { f } _ { i } } } \end{aligned}
\]
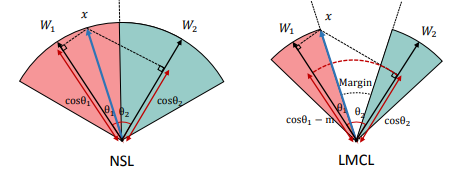
CosFace
相关文献:
- 《Cosface: Large margin cosine loss for deep face recognition》
\[L _ { l m c } = \frac { 1 } { N } \sum _ { i } - \log \frac { e ^ { s \left( \cos \left( \theta _ { y _ { i } , i } \right) - m \right) } } { e ^ { s \left( \cos \left( \theta _ { y _ { i } } , i \right) - m \right) } + \sum _ { j \neq y _ { i } } e ^ { s \cos \left( \theta _ { j , i } \right) } }
\]
\[\begin{aligned} \text { subject to } \\ W & = \frac { W ^ { * } } { \left\| W ^ { * } \right\| } \\ x & = \frac { x ^ { * } } { \left\| x ^ { * } \right\| } \\ \cos \left( \theta _ { j } , i \right) & = W _ { j } ^ { T } x _ { i } \end{aligned}
\]
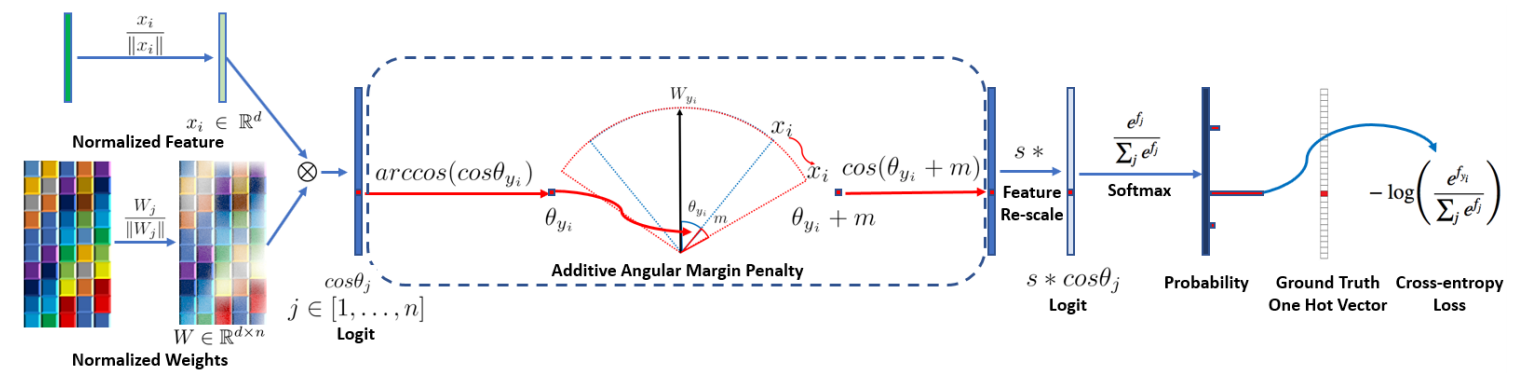
ArcFace
相关文献:
- 《Arcface: Additive angular margin loss for deep face recognition》
\[L = - \frac { 1 } { N } \sum _ { i = 1 } ^ { N } \log \frac { e ^ { s \left( \cos \left( \theta _ { y _ { i } } + m \right) \right) } } { e ^ { s \left( \cos \left( \theta _ { y _ { i } } + m \right) \right) } + \sum _ { j = 1 , j \neq y _ { i } } ^ { n } e ^ { s \cos \theta _ { j } } }
\]
Softmax及其变种
L2-Softmax
相关文献:
- 《L2-constrained softmax loss for discriminative face verification》
\[\begin{array} { l l } { \text { minimize } } & { - \frac { 1 } { M } \sum _ { i = 1 } ^ { M } \log \frac { e ^ { W _ { y _ { i } } ^ { T } f \left( \mathbf { x } _ { i } \right) + b _ { y _ { i } } } } { \sum _ { j = 1 } ^ { C } e ^ { W _ { j } ^ { T } f \left( \mathbf { x } _ { i } \right) + b _ { j } } } } \\ { \text { subject to } } & { \left\| f \left( \mathbf { x } _ { i } \right) \right\| _ { 2 } = \alpha , \forall i = 1,2 , \ldots M } \end{array}
\]
Normface
相关文献:
- 《NormFace: L2 Hypersphere Embedding for Face Verification》
\[\mathcal { L } _ { S' } = - \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \log \frac { e ^ { s \tilde { W } _ { y _ { i } } ^ { T } \tilde { \mathbf { f } } _ { i } } } { \sum _ { j = 1 } ^ { n } e ^ { s \tilde { W } _ { j } ^ { T } \mathbf { f } _ { i } } }
\]
\[\tilde { \mathbf { x } } = \frac { \mathbf { x } } { \| \mathbf { x } \| _ { 2 } } = \frac { \mathbf { x } } { \sqrt { \sum _ { i } \mathbf { x } _ { i } ^ { 2 } + \epsilon } }
\]
CoCo loss
相关文献:
- 《Rethinking feature discrimination and polymerization for large-scale recognition》
\[\mathcal { L } ^ { C O C O } \left( \boldsymbol { f } ^ { ( i ) } , \boldsymbol { c } _ { k } \right) = - \sum _ { i \in \mathcal { B } , k } t _ { k } ^ { ( i ) } \log p _ { k } ^ { ( i ) } = - \sum _ { i \in \mathcal { B } } \log p _ { l _ { i } } ^ { ( i ) }
\]
\[\hat { \boldsymbol { c } } _ { k } = \frac { \boldsymbol { c } _ { k } } { \left\| \boldsymbol { c } _ { k } \right\| } , \hat { \boldsymbol { f } } ^ { ( i ) } = \frac { \alpha \boldsymbol { f } ^ { ( i ) } } { \left\| \boldsymbol { f } ^ { ( i ) } \right\| } , p _ { k } ^ { ( i ) } = \frac { \exp \left( \hat { \boldsymbol { c } } _ { k } ^ { T } \cdot \hat { \boldsymbol { f } } ^ { ( i ) } \right) } { \sum _ { m } \exp \left( \hat { \boldsymbol { c } } _ { m } ^ { T } \cdot \hat { \boldsymbol { f } } ^ { ( i ) } \right) }
\]
Ring loss
相关文献:
- 《Ring loss: Convex feature normalization for face recognition》
\[L _ { R } = \frac { \lambda } { 2 m } \sum _ { i = 1 } ^ { m } \left( \left\| \mathcal { F } \left( \mathbf { x } _ { i } \right) \right\| _ { 2 } - R \right) ^ { 2 }
\]
参考文献