虚树入门
鬼知道为什么我又要开这个新坑,就挺离谱的。
虚树这东西是在订正模拟赛题目时遇到的,正解需要这个东西,但是我不会...
然后去学了一下感觉这个东西本身也不是很难,当然需要结合着题目来讲,就会很容易懂了。
我们引入一道例题,并配合题目进行讲解。
CF613D Kingdom and its Cities
有一颗 \(n\) 个节点的树,一些节点设为了重要节点。
重要节点是不会被选中的。重要节点之外的节点就是非重要节点,选到这些节点之后,与之相连的边就会断掉,求能否选择一些节点让重要节点两两不连通。
重要节点会选择 \(m\) 次,每次选择 \(k\) 个节点。
\(\sum k \leq 10^5\) , \(n\leq 10^5\)
首先考虑不行的情况,如果有两个重要节点之间是直接连边的,那么就是不行的,否则都是行的。
考虑怎么转移做这个东西,分类讨论一下。
当 \(u\) 为关键节点的时候,将每个没有断开的子孙全部断开就是了。
当 \(u\) 不为关键节点时,如果他有多个关键节点都没有断开,那么就将他自己断开就是了。
这么做的话每次都要遍历一遍全树,这让我们的复杂度变得不可接受,为 \(O(nm)\) 。
考虑到其实对于选择的点不同有些点是可以不用选上的,我们是否可以将这些点给删去?
当然可以。
我们考虑哪些节点是无所谓的,发现每次其实只会更你重要节点的 \(\text{LCA}\) 有关,那么你就只需要保留的是这些节点以及它们的 \(\text{LCA}\) 就行了。
这么删去无关节点之后形成的树就是虚树。
虚树建立出来之后就会让你的复杂度变小这是显而易见的。
然后我的虚树的建立可能比较不一样,这是从神仙 \(\color{red}{\text{p}}\color{black}{\text{_b_p_b}}\) 那里学到的。
把点按dfn排序,相邻点的lca丢进去,再排序,每个点在虚树上的父亲就是自己和前驱的lca。
很妙,这个东西的证明就不证明了吧,联合 \(dfn\) 序想一下就知道这是正确的。
然后这个东西还很好写,这样做你就可以通过本题目了。
const int N = 5e5;
int n, m, num, cnt, q, siz[N], dep[N], dfn[N], id[N], ask[N], f[N];
int top[N], son[N], mark[N], tp;
vector<int> ver[N];
int cmp(int a, int b) { return dfn[a] < dfn[b]; }
void dfs1(int x, int fa) {
dfn[x] = ++cnt;
id[cnt] = x;
siz[x] = 1;
dep[x] = dep[fa] + 1;
for (int i = 0; i < ver[x].size(); i++) {
int to = ver[x][i];
if (to == fa)
continue;
f[to] = x;
dfs1(to, x);
siz[x] += siz[to];
if (siz[to] > siz[son[x]])
son[x] = to;
}
}
void dfs2(int now, int x) {
top[now] = x;
if (son[now])
dfs2(son[now], x);
for (int i = 0; i < ver[now].size(); i++) {
int to = ver[now][i];
if (to == f[now] || to == son[now])
continue;
dfs2(to, to);
}
}
int LCA(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] >= dep[top[y]])
x = f[top[x]];
else
y = f[top[y]];
}
return dep[x] < dep[y] ? x : y;
}
int dp[N], dp2[N];
vector<int> p[N];
int getans(int x) {
int ret = 0;
for (int i = 0; i < p[x].size(); i++)
ret += getans(p[x][i]);
if (mark[x]) {
for (int i = 0; i < p[x].size(); i++)
if (mark[p[x][i]])
ret++;
} else {
int bel = 0;
for (int i = 0; i < p[x].size(); i++)
if (mark[p[x][i]])
bel++;
if (bel > 1)
ret++;
else if (bel == 1)
mark[x] = 1;
}
return ret;
}
signed main() {
n = read();
for (int i = 1; i < n; i++) {
int u = read(), v = read();
ver[u].push_back(v);
ver[v].push_back(u);
}
dfs1(1, 0);
dfs2(1, 1);
q = read();
while (q--) {
m = read();
for (int i = 1; i <= m; i++)
ask[i] = read(), mark[ask[i]] = 1;
int fl = 0;
for (int i = 1; i <= m; i++)
if (mark[f[ask[i]]]) {
fl = 1;
break;
}
if (fl) {
for (int i = 1; i <= m; i++)
mark[ask[i]] = 0;
write(-1);
putc('\n');
continue;
}
num = m;
sort(ask + 1, ask + num + 1, cmp);
for (int i = 2; i <= m; i++) {
int lca = LCA(ask[i], ask[i - 1]);
if (lca != ask[i] && lca != ask[i - 1])
ask[++num] = lca;
}
sort(ask + 1, ask + num + 1);
tp = num;
num = unique(ask + 1, ask + num + 1) - (ask + 1);
sort(ask + 1, ask + num + 1, cmp);
for (int i = 2; i <= num; i++) {
int lca = LCA(ask[i], ask[i - 1]);
p[lca].push_back(ask[i]);
}
write(getans(ask[1]));
putc('\n');
for (int i = 1; i <= num; i++)
mark[ask[i]] = 0;
for (int i = 1; i <= num; i++)
p[ask[i]].clear();
}
flush();
return 0;
}
P4103 [HEOI2014]大工程
一颗边权为单位边权的 \(n\) 个节点的树,执行 \(q\) 次操作,每次操作选择 \(k\) 个点,在 \(k\) 个节点中两两建通道,通带的代价为树上两点的距离。
求新通道中代价和,代价最小值,代价最大值。
\(n \leq 10^6\) , \(\sum k\leq 2\times 10^6\)
遇到这种题目现在就已经很明显了吧...
先考虑朴素的转移,进行树上 \(dp\) 。
发现可行,但是中途发现是有很多无关节点的,仍然只与选中点,以及它们的 \(\text{LCA}\) 有关,那么建立出虚树,然后进行虚树 \(dp\) 就行了。
这个 \(dp\) 太简单就不讲了。
简单来说一个思路就是考虑以父亲为中转站,然后儿子之间进行配对。
const int N = 2e6, INF = 2e9;
int n, q, m, num, cnt, dfn[N], siz[N], son[N], f[N], top[N], dep[N];
int ask[N], mark[N], ans1, ans2, ans3;
vector<int> ver[N], p[N];
void dfs1(int x, int fa) {
dfn[x] = ++cnt;
siz[x] = 1;
dep[x] = dep[fa] + 1;
for (int i = 0; i < ver[x].size(); i++) {
int to = ver[x][i];
if (to == fa)
continue;
f[to] = x;
dfs1(to, x);
siz[x] += siz[to];
if (siz[to] > siz[son[x]])
son[x] = to;
}
}
void dfs2(int now, int x) {
top[now] = x;
if (son[now])
dfs2(son[now], x);
for (int i = 0; i < ver[now].size(); i++) {
int to = ver[now][i];
if (to == son[now] || to == f[now])
continue;
dfs2(to, to);
}
}
int LCA(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] >= dep[top[y]])
x = f[top[x]];
else
y = f[top[y]];
}
return dep[x] < dep[y] ? x : y;
}
int cmp(int x, int y) { return dfn[x] < dfn[y]; }
int mx[N], mn[N], s[N], g[N];
void dp(int x) {
s[x] = mark[x];
g[x] = 0;
if (mark[x])
mx[x] = mn[x] = 0;
else
mx[x] = -INF, mn[x] = INF;
for (int i = 0; i < p[x].size(); i++) {
int to = p[x][i];
dp(to);
int l = dep[to] - dep[x];
ans1 += (g[x] + s[x] * l) * s[to] + g[to] * s[x];
s[x] += s[to];
g[x] += g[to] + l * s[to];
ans2 = min(ans2, mn[x] + mn[to] + l);
ans3 = max(ans3, mx[x] + mx[to] + l);
mn[x] = min(mn[x], mn[to] + l);
mx[x] = max(mx[x], mx[to] + l);
}
}
signed main() {
n = read();
for (int i = 1; i < n; i++) {
int a = read(), b = read();
ver[a].push_back(b);
ver[b].push_back(a);
}
dfs1(1, 0);
dfs2(1, 1);
q = read();
while (q--) {
m = read();
for (int i = 1; i <= m; i++)
ask[i] = read(), mark[ask[i]] = 1;
sort(ask + 1, ask + m + 1, cmp);
num = m;
for (int i = 2; i <= m; i++) {
int lca = LCA(ask[i], ask[i - 1]);
if (lca != ask[i] && lca != ask[i - 1])
ask[++num] = lca;
}
sort(ask + 1, ask + num + 1);
num = unique(ask + 1, ask + num + 1) - (ask + 1);
sort(ask + 1, ask + num + 1, cmp);
for (int i = 2; i <= num; i++) {
int lca = LCA(ask[i], ask[i - 1]);
p[lca].push_back(ask[i]);
}
ans1 = 0;
ans2 = INF;
ans3 = -INF;
dp(ask[1]);
printf("%lld %lld %lld\n", ans1, ans2, ans3);
for (int i = 1; i <= num; i++)
p[ask[i]].clear(), mark[ask[i]] = 0;
}
return 0;
}
P3233 [HNOI2014]世界树
一个边权均为 \(1\) 的 \(n\) 个节点的树。
\(q\) 次操作,每次选定 \(m\) 个节点作为特殊节点,我们想找出每个特殊节点可以控制的节点数目,对于每个节点,他被离他最近的特殊节点支配。
\(n \leq 3\times 10^5\) , \(\sum m \leq 3\times 10^5\)
恶心的要死的题。
这道题依旧还是很明显的暗示了你往虚树上想。
然后这道题的难点不在于虚树,在于想到虚树后你怎么做这个东西。
首先我们考虑对于我们选中的这些节点他们的答案是由哪里来的。
两个地方的贡献,一个是虚树上节点的贡献,一个是虚树外的节点的贡献。
我们首先考虑虚树上的节点的贡献,这个东西其实很好算的。
首先我们考虑说对于一个议事处,首先他本身肯定是被他自己控制的。
然后这个就确定了,但是虚树上就是会有非议事处节点,这个时候你就要去更新这个东西。
这个很明显,他只会被在虚树上的儿子和父亲更新。
然后这个你可以通过两个 \(\text{dfs}\) 解决。
我们思考一下对于虚树外的节点怎么贡献他们的答案。
先对这个虚树外的节点分个类,有两种可能情况。
节点是在虚树上某个节点 \(u\) 的子树内,那很明显的是这些节点都是被 \(u\) 控制的。
那我们让 \(u\) 的子树大小减去他的子节点方向上的所有节点数就是这些节点的贡献。
我们考虑怎么计算这个答案,等价于计算 \(u\) 在儿子 \(v\) 方向上的直接儿子。
这个很明显可以转化为减去 \(v\) 的 \(dep_v-dep_u-1\) 级祖先的子树大小。
这个东西很明显可以长链,重剖,倍增乱搞。
然后考虑第二种情况,对于节点是在虚树上节点 \(u\) 和儿子 \(v\) 之间的。
那么这个东西就是说你是有可能是控制儿子的那个点控制你,也有可能是控制父亲的那个点控制你。
然后你就是要去判断是到哪个节点的时候你这个东西是属于父亲那边的,其他是属于儿子那边的。
那么很显然的你只要找到一个分界点,满足的是上面都属于父亲那边,下面都属于儿子那边。
这个操作让你想到了二分,然后他也是可以二分的。
还有一个细节需要注意。
我们要保证所有的节点都被算到贡献,所以你的虚树根节点一定要是从深度最低的根节点开始的。
而你的所给的虚树节点中建出来的虚树不一定是从根节点开始的。
比如只有一个节点的时候。
然后样例就有这么一个情况还是比较良心的,但我还是调了一天 。
然后就这么做,然后思路就是这样了,写起来难写的要死。
也可能是我太菜了,所以才觉得难写。

const int N = 1e6;
int n, m, q, cnt, dfn[N], dep[N], top[N], siz[N], ask[N], son[N], f[N];
int num, tot, mark[N], dp[N], in[N], pl[N], ans[N], g[N];
vector<int> ver[N], p[N];
void dfs1(int x, int fa) {
dfn[x] = ++cnt;
dep[x] = dep[fa] + 1;
siz[x] = 1;
for (int i = 0; i < ver[x].size(); i++) {
int to = ver[x][i];
if (to == fa)
continue;
f[to] = x;
dfs1(to, x);
siz[x] += siz[to];
if (siz[to] > siz[son[x]])
son[x] = to;
}
}
void dfs2(int now, int x) {
top[now] = x;
in[now] = ++tot;
pl[tot] = now;
if (son[now])
dfs2(son[now], x);
for (int i = 0; i < ver[now].size(); i++) {
int to = ver[now][i];
if (to == f[now] || to == son[now])
continue;
dfs2(to, to);
}
}
int LCA(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] >= dep[top[y]]) // ok
x = f[top[x]]; // ok
else
y = f[top[y]];
}
return dep[x] < dep[y] ? x : y; // ok
}
int jump(int x, int k) {
int rt = 1;
// cout << "cnmSb\n";
while (k >= in[x] - in[top[x]] + 1 && x != rt) { // ok
k -= (in[x] - in[top[x]] + 1); // ok
x = f[top[x]]; // ok
} // ok
return pl[in[x] - k]; // ok
}
int getdis(int x, int y) { return dep[x] + dep[y] - (dep[LCA(x, y)] << 1); }
void get1(int x) {
if (mark[x])
dp[x] = x;
else
dp[x] = -1;
for (int i = 0; i < p[x].size(); i++) {
int to = p[x][i];
get1(to);
if (dp[to] != -1) {
if (dp[x] == -1) {
dp[x] = dp[to]; // ok
} else {
int d1 = getdis(x, dp[to]), d2 = getdis(x, dp[x]); // ok
if (d1 < d2 || (d1 == d2 && dp[to] < dp[x]))
dp[x] = dp[to]; // ok
}
}
}
}
// ok
void get2(int x) {
for (int i = 0; i < p[x].size(); i++) {
int to = p[x][i];
if (dp[to] == -1) {
dp[to] = dp[x]; // ok
} else {
int d1 = getdis(to, dp[x]); // ok
int d2 = getdis(to, dp[to]); // ok
if (d1 < d2 || (d1 == d2 && dp[x] < dp[to]))
dp[to] = dp[x]; // ok
}
get2(to);
}
}
// ok
void get3(int x) {
ans[dp[x]] += siz[x];
for (int i = 0; i < p[x].size(); i++) {
int to = p[x][i];
ans[dp[x]] -= siz[jump(to, dep[to] - dep[x] - 1)];
get3(to);
}
}
// ok
void get4(int x) {
for (int i = 0; i < p[x].size(); i++) {
int to = p[x][i];
if (dp[x] != dp[to]) {
int d1 = getdis(x, dp[x]); // ok
int d2 = getdis(to, dp[to]); // ok
int len = dep[to] - dep[x] - 1; // ok
int l = 0, r = len, p = len + 1; // ok
while (l <= r) {
int mid = (l + r) >> 1;
if (d1 + mid < d2 + len + 1 - mid ||
(d1 + mid == d2 + len + 1 - mid && dp[x] < dp[to]))
p = mid, l = mid + 1; // ok
else
r = mid - 1; // ok
}
if (p == 0)
ans[dp[to]] += siz[jump(to, len)] - siz[to]; // ok
else if (p == len + 1)
ans[dp[x]] += siz[jump(to, len)] - siz[to]; // ok
else {
ans[dp[x]] += siz[jump(to, len)] - siz[jump(to, len - p)]; // ok
ans[dp[to]] += siz[jump(to, len - p)] - siz[to]; // ok
}
} else {
ans[dp[x]] += siz[jump(to, dep[to] - dep[x] - 1)] - siz[to]; // ok
}
get4(to);
}
}
// ok
int cmp(int x, int y) { return dfn[x] < dfn[y]; }
signed main() {
n = read();
for (int i = 1; i < n; i++) {
int a = read(), b = read();
ver[a].push_back(b);
ver[b].push_back(a);
}
dfs1(1, 0);
dfs2(1, 1);
q = read();
while (q--) {
int fl = 0;
m = read();
for (int i = 1; i <= m; i++)
ask[i] = read(), mark[ask[i]] = 1, g[i] = ask[i];
sort(ask + 1, ask + m + 1, cmp);
num = m;
for (int i = 2; i <= m; i++) {
int lca = LCA(ask[i], ask[i - 1]);
if (ask[i] != lca && ask[i - 1] != lca)
ask[++num] = lca;
}
sort(ask + 1, ask + num + 1);
// cout << "cnmSb\n";
num = unique(ask + 1, ask + num + 1) - (ask + 1); // ok
sort(ask + 1, ask + num + 1, cmp);
for (int i = 2; i <= num; i++) {
int lca = LCA(ask[i], ask[i - 1]);
p[lca].push_back(ask[i]);
}
if (ask[1] != 1)
p[1].push_back(ask[1]);
get1(1);
get2(1);
get3(1);
get4(1);
/*
for(int i=1;i<=m;i++){
printf("%lld ",dp[g[i]]);
}
printf("\n");
*/
for (int i = 1; i <= m; i++) {
printf("%lld ", ans[g[i]]);
}
printf("\n");
for (int i = 1; i <= num; i++) {
mark[ask[i]] = 0;
p[ask[i]].clear();
ans[ask[i]] = 0;
dp[ask[i]] = 0;
}
p[1].clear();
dp[1] = 0;
ans[1] = 0;
mark[1] = 0;
}
return 0;
}
P2495 [SDOI2011]消耗战
给定一棵𝑛个点的树(边带权)以及若干组关键点,对每一组求删边的最少代价(删边的代价为边权)可以使关键点与1 号节点不连通。
\(𝑛≤2.5×10^5,∑𝑘 ≤5×10^5\) 。
这道题同样的还是建立虚树。
仍然考虑我们去进行 \(dp\) ,我们考虑的时候我们要将一个子树的答案向上传,所以就以子树为状态设立转移。
设立 \(dp_u\) 表示在子树 \(u\) 中的答案。
考虑当点 \(u\) 为关键点的时候,他是必须断的,而他断了那么其实下面的点就不用在断了,所以这个时候 \(dp_u=mn_u\) 。
其中 \(mn_u\) 表示的是 \(u\) 到 \(1\) 最小的边权。
考虑不是关键点的时候,可断可不断,那么我们将这个与他子树答案和进行比较取更小的答案就行了。
也就是 \(dp_u=\min(\sum dp_v,mn_u)\) 。
然后就可以解决这个问题了。
顺便附赠一组数据方便调试
input:
10
1 2 6432
2 3 9694
3 4 9714
4 5 8890
4 6 9170
1 7 6361
1 8 1627
2 9 9824
7 10 9947
5
3 4 7 2
5 7 2 10 6 3
5 3 7 4 8 10
3 3 2 10
2 6 8
output:
12793
12793
14420
12793
8059
const int N = 1e6, INF = 2e16;
int n, q, m, num, cnt, son[N], top[N], siz[N], dfn[N], dep[N], f[N], mn[N];
int ask[N], mark[N], dp[N];
vector<int> ver[N], val[N], p[N];
void dfs1(int x, int fa) {
siz[x] = 1;
dfn[x] = ++cnt;
dep[x] = dep[fa] + 1;
for (int i = 0; i < ver[x].size(); i++) {
int to = ver[x][i];
int w = val[x][i];
if (to == fa)
continue;
f[to] = x;
mn[to] = min(mn[x], w);
dfs1(to, x);
siz[x] += siz[to];
if (siz[to] > siz[son[x]])
son[x] = to;
}
}
void dfs2(int now, int x) {
top[now] = x;
if (son[now])
dfs2(son[now], x);
for (int i = 0; i < ver[now].size(); i++) {
int to = ver[now][i];
if (to == f[now] || to == son[now])
continue;
dfs2(to, to);
}
}
int LCA(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] <= dep[top[y]])
y = f[top[y]];
else
x = f[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
int cmp(int x, int y) { return dfn[x] < dfn[y]; }
void getans(int x) {
// cout << x << " " << mark[x] << " " << dp[x] << " " << mn[x] << "\n";
int ret = 0;
for (int i = 0; i < p[x].size(); i++) {
int to = p[x][i];
getans(to);
// if (x == 1)
// cout << to << " " << dp[to] << "\n";
ret = ret + dp[to];
}
if (mark[x]) {
dp[x] = mn[x];
} else {
dp[x] = min(mn[x], ret);
}
// cout << x<<f[x] << " " << mark[x] << " " << dp[x] << " " << mn[x] << "\n";
}
signed main() {
n = read();
for (int i = 1; i <= n; i++)
mn[i] = INF;
for (int i = 1; i < n; i++) {
int u = read(), v = read(), w = read();
ver[u].push_back(v);
val[u].push_back(w);
ver[v].push_back(u);
val[v].push_back(w);
}
dfs1(1, 0);
dfs2(1, 1);
q = read();
while (q--) {
m = read();
for (int i = 1; i <= m; i++)
ask[i] = read(), mark[ask[i]] = 1;
sort(ask + 1, ask + m + 1, cmp);
num = m;
for (int i = 2; i <= m; i++) {
int lca = LCA(ask[i], ask[i - 1]);
if (lca != ask[i] && lca != ask[i - 1])
ask[++num] = lca;
}
sort(ask + 1, ask + num + 1);
num = unique(ask + 1, ask + num + 1) - (ask + 1);
sort(ask + 1, ask + num + 1, cmp);
for (int i = 2; i <= num; i++) {
int lca = LCA(ask[i], ask[i - 1]);
p[lca].push_back(ask[i]);
}
getans(ask[1]);
printf("%lld\n", dp[ask[1]]);
for (int i = 1; i <= num; i++)
dp[ask[i]] = 0, mark[ask[i]] = 0, p[ask[i]].clear();
}
return 0;
}
P4242 树上的毒瘤
一颗 \(n\) 个节点的树,每个点都有自己的权值 \(c\) 。进行 \(q\) 次操作,操作有两种。
一种是改变两个节点路径之间节点的权值。
一种是查询给定点集中,所有点到其他点的颜色段数和。
$n , q \leq 10^5 $ , \(\sum m \leq 2\times 10^5\)
又是超级难写题。
个人认为这道题的思路其实是很简单的。
首先你要会求颜色段数,这个很简单对吧,就直接树剖加上线段树就完事了,也就是 这道题 。
然后会了这个我们就可以快速求出树上任意两点之间的颜色段数。
首先这题还是老套路的虚树模式,直接先建出虚树来。
考虑怎么做题,我们考虑是肯定要设立一个 \(dp\) 。
但是现在没啥思路,我们就去看看建出来的虚树。
这个树你肯定要给他赋一个边权但是边权怎么赋值?
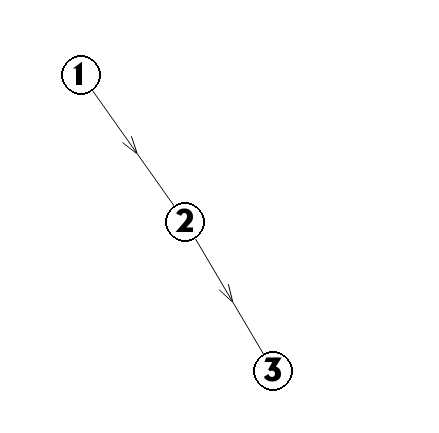
你考虑下图。
我们希望做到的是点 \(1\) 到点 \(2\) 的边权加上点 \(2\) 到点 \(3\) 的边权之间是有某种关系的,最好是能相等的。
但是因为可能父亲的颜色段与父亲的父亲产生冲突,这个是会有影响的。
那我们直接不管父亲的颜色段,将边权设为两点颜色段数减去 \(1\) 。
最后需要用的时候我们在加上 \(1\) 就好了。
然后这个东西就很对了。
那么一条路径的权值就是边权和加上 \(1\) 。
然后你这个时候在统计路径就变成了一个经典的换根 \(dp\) 。
然后你考虑你一个点向 \(m\) 个点找路径那你就加上 \(m\) 就好了。
然后就用树剖加上换根 \(dp\) 写完了这道题。
const int N = 3e5;
int n, q, m, num, cnt, c[N], siz[N], dep[N], f[N], son[N], top[N];
int dfn[N], col[N], dfn2[N], tot, aske[N], mark[N], id[N];
vector<int> ver[N], p[N];
void dfs1(int x, int fa) {
siz[x] = 1;
dfn2[x] = ++tot;
dep[x] = dep[fa] + 1;
f[x] = fa;
for (int i = 0; i < ver[x].size(); i++) {
int to = ver[x][i];
if (to == fa)
continue;
dfs1(to, x);
siz[x] += siz[to];
if (siz[to] > siz[son[x]])
son[x] = to;
}
}
void dfs2(int now, int x) {
top[now] = x;
dfn[now] = ++cnt;
col[cnt] = c[now];
if (son[now])
dfs2(son[now], x);
for (int i = 0; i < ver[now].size(); i++) {
int to = ver[now][i];
if (to == f[now] || to == son[now])
continue;
dfs2(to, to);
}
}
int LCA(int x, int y) {
while (top[x] != top[y]) {
if (dep[top[x]] <= dep[top[y]])
y = f[top[y]];
else
x = f[top[x]];
}
return dep[x] < dep[y] ? x : y;
}
int s[N], tag[N];
int ls(int p) { return p << 1; }
int rs(int p) { return p << 1 | 1; }
void push_up(int p, int mid) {
s[p] = s[ls(p)] + s[rs(p)];
if (col[mid] == col[mid + 1])
s[p]--;
}
void pushdown(int p, int mid) {
tag[ls(p)] = tag[rs(p)] = tag[p];
col[mid] = col[mid + 1] = tag[p];
s[ls(p)] = 1, s[rs(p)] = 1;
tag[p] = 0;
}
void build(int p, int l, int r) {
if (l == r) {
s[p] = 1;
return;
}
int mid = (l + r) >> 1;
build(ls(p), l, mid), build(rs(p), mid + 1, r);
push_up(p, mid);
}
void update(int p, int l, int r, int nx, int ny, int k) {
if (nx <= l and r <= ny) {
s[p] = 1;
col[l] = col[r] = tag[p] = k;
return;
}
int mid = (l + r) >> 1;
if (tag[p])
pushdown(p, mid);
if (nx <= mid)
update(ls(p), l, mid, nx, ny, k);
if (ny > mid)
update(rs(p), mid + 1, r, nx, ny, k);
push_up(p, mid);
}
int ask(int p, int l, int r, int nx, int ny) {
if (nx <= l && r <= ny)
return s[p];
int mid = (l + r) >> 1, ans = 0;
if (tag[p])
pushdown(p, mid);
if (nx <= mid)
ans = ask(ls(p), l, mid, nx, ny);
if (ny > mid)
ans += ask(rs(p), mid + 1, r, nx, ny);
if (nx <= mid && ny > mid) {
if (col[mid] == col[mid + 1])
ans--;
}
return ans;
}
void addtree(int x, int y, int val) {
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]])
swap(x, y);
update(1, 1, n, dfn[top[x]], dfn[x], val);
x = f[top[x]];
}
if (dep[x] > dep[y])
swap(x, y);
update(1, 1, n, dfn[x], dfn[y], val);
}
int asktree(int x, int y) {
int ans = 0, u = x, v = y;
while (top[x] != top[y]) {
if (dep[top[x]] < dep[top[y]])
swap(x, y);
ans = (ans + ask(1, 1, n, dfn[top[x]], dfn[x]));
x = f[top[x]];
}
if (dep[x] > dep[y])
swap(x, y);
ans = (ans + ask(1, 1, n, dfn[x], dfn[y]));
while (top[u] != top[v]) {
if (dep[top[u]] < dep[top[v]])
swap(u, v);
if (col[dfn[top[u]]] == col[dfn[f[top[u]]]])
--ans;
u = f[top[u]];
}
return ans;
}
int cmp(int x, int y) { return dfn2[x] < dfn2[y]; }
int dp[N], dp2[N], sz[N];
void get1(int x) {
if (mark[x])
sz[x] = 1;
else
sz[x] = 0;
dp[x] = 0;
for (int i = 0; i < p[x].size(); i++) {
int to = p[x][i];
int val = asktree(to, x) - 1;
get1(to);
sz[x] += sz[to];
dp[x] += dp[to] + val * sz[to];
}
}
void get2(int x) {
for (int i = 0; i < p[x].size(); i++) {
int to = p[x][i];
int val = asktree(to, x) - 1;
dp2[to] = dp2[x] + (m - 2 * sz[to]) * val;
get2(to);
}
}
signed main() {
n = read(), q = read();
for (int i = 1; i <= n; i++)
c[i] = read();
for (int i = 1; i < n; i++) {
int a = read(), b = read();
ver[a].push_back(b);
ver[b].push_back(a);
}
dfs1(1, 0);
dfs2(1, 1);
build(1, 1, n);
while (q--) {
int op = read();
if (op == 1) {
int u = read(), v = read(), y = read();
addtree(u, v, y);
} else {
m = read();
for (int i = 1; i <= m; i++)
aske[i] = read(), mark[aske[i]] = 1, id[i] = aske[i];
sort(aske + 1, aske + m + 1, cmp);
num = m;
for (int i = 2; i <= m; i++) {
int lca = LCA(aske[i], aske[i - 1]);
if (lca != aske[i] && lca != aske[i - 1])
aske[++num] = lca;
}
sort(aske + 1, aske + num + 1);
num = unique(aske + 1, aske + num + 1) - (aske + 1);
sort(aske + 1, aske + num + 1, cmp);
for (int i = 2; i <= num; i++) {
int lca = LCA(aske[i], aske[i - 1]);
p[lca].push_back(aske[i]);
}
get1(aske[1]);
dp2[aske[1]] = dp[aske[1]];
get2(aske[1]);
for (int i = 1; i <= m; i++)
write(dp2[id[i]] + m), putc(' ');
putc('\n');
for (int i = 1; i <= num; i++)
p[aske[i]].clear(), mark[aske[i]] = 0, dp2[aske[i]] = 0,
dp[aske[i]] = 0, sz[aske[i]] = 0, id[i] = 0;
}
}
flush();
return 0;
}
结语
其实如果看了这篇文章后可以发现的是,作者都只是写了一些简单的板子题,没有思维的那种。
真正的难题在于想到虚树,建虚树。
作者在这篇文章前的言论是有错误的,虚树的建立其实才是关键,不应该有偏驳,这是在写完这些题去做升级题的时候了解到的。
希望大家看过这个垃圾文章能巩固基础( )
然后这一切都还是因为作者还太菜了。
有幸的话,作者将会把这篇文章升级,加入更多虚树拓展。
但现在很抱歉,这篇文章鸽子了。


