莫队算法
莫队算法
普通莫队
1.例题:小Z的袜子
2.能够解决怎么样的问题?
莫队算法能够将一些不强制在线的区间查询问题,使用离线分块的思想,然后利用双指针,将算法的复杂度降低。
3.算法实现原理:
因为是不带修改的,所以我们可以用双关键字进行排序,第一关键字是左端点所在块的编号,第二关键字是右端点的位置,编号越靠前越优先,右端点也是越靠前越优先。进行排序完之后,我们就可以直接用双指针暴力更新答案了。
4.莫队常数优化:如果块号相同,那么我们可以分块的奇偶性来排序,如果为奇数,那么按右端点升序排序,如果为偶数,那么按右端点降序排序。
5.复杂度分析:
莫队算法的优势就在于分块排序优化了复杂度。假设范围大小为n,有m个询问,m=O(n)。如果我们按照读入的顺序来枚举每个询问,或者按照左端点排序和右端点排序,那么你可以想象到L和R疯狂转移的情况,这样时间复杂度最坏依然是O(nm)=\(O(n^{2})\)
而使用分块排序,再分析相邻查询转移次数。我们假设块的长度是B,块的总数是\(\frac{n}{B}\)。
① 对于L的移动:同一块内最多移动B次。若下一个询问与当前的L不在同一块,那么最长只需要2B的长度即可到达目标端点,计算量最高2mB。
② 对于R的移动:R当L在同一块内时有序,所以枚举完一个块,R最多共移动n次,换块时,再至多移动n次。总共有\(\frac{n}{B}\)个块,计算量最高为\(\frac{n}{B}(n + n) = \frac{2n^{2}}{B}\)。
合起来总的复杂度为\(2mB + \frac{2n^{2}}{B}\),当取\(B = \sqrt{\frac{n^{2} }{m} }\)时复杂度最低:\(O(n\sqrt{n})\)。当m较小时取\(\sqrt{n}\)即可。
6.例题代码:
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define lc p<<1
#define rc p<<1|1
#define int long long
#define vc vector<char>
#define vi vector<int>
#define vvi vector<vector<int>>
#define vpi vector<pair<int,int>>
#define vvc vector<vector<char>>
#define vvpi vector<vector<pair<int,int>>>
typedef long long ll;
typedef tuple<int,int,int> tp;
typedef pair<int,int> PII;
typedef pair<ll,pair<ll,ll>> PIII;
typedef pair<ll,pair<ll,pair<ll,ll>>> pIIII;
const int N = 1e5 + 7;
const int inf = 0x3f3f3f3f;
const int mod = 998244353;
const int none = -1e9 - 1;
int B,n,m,k;
struct query {
int l,r,id;
ll p,c;
query(){};
query(int l0,int r0,int id0) : l(l0),r(r0),id(id0) {
this->p = 0;
this->c = (r - l + 1)*(r - l)/2;
}
bool operator <(const query &a) const {
if(l/B != a.l/B) return l < a.l;
if(l/B % 2 == 1) return r < a.r;
return r > a.r;
}
}Q[N];
void solve() {
int n,q;cin >> n >> q;
vi a(n + 1);
vector<ll> color(n + 1);
B = sqrt(n);
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= q; i++) {
int l,r;cin >> l >> r;
Q[i] = query(l,r,i);
}
sort(Q + 1,Q + 1 + q);
// for(int i = 1; i <= q; i++) {
// cout << Q[i].l << " " << Q[i].r << "\n";
// }
auto add = [&](int x,query &t) {
t.p += color[x]++;
};
auto del = [&](int x,query &t) {
t.p -= --color[x];
};
Q[0] = query(0,0,0);
for(int i = 1,l = 1,r = 0; i <= q; i++) {
int l1 = Q[i].l,r1 = Q[i].r,id = Q[i].id;
Q[i].p = Q[i - 1].p;
while(l > l1) add(a[--l],Q[i]);
while(r < r1) add(a[++r], Q[i]);
while(l < l1) del(a[l++],Q[i]);
while(r > r1) del(a[r--],Q[i]);
}
sort(Q + 1,Q + 1 + q,[&](query &t1,query &t2) {
return t1.id < t2.id;
});
for(int i = 1; i <= q; i++) {
int gcd = __gcd(Q[i].p,Q[i].c);
if(gcd != 0) Q[i].p /= gcd,Q[i].c /= gcd;
if(Q[i].p == 0) cout << "0/1\n";
else cout << Q[i].p << "/" << Q[i].c << "\n";
}
}
signed main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
int t = 1;
//cin >> t;
while(t--) {
solve();
}
//system("pause");
return 0;
}
/*
Do smth instead of nothing and stay organized
Don't get stuck on one approach
*/
带修莫队
- 例题:数颜色
- 算法分析:由于多了一个时间戳,所以不能按照原来的排序方式,否则时间复杂度就会回到\(O(n^{2})\),所以我们要改变排序的规则,第一关键字是左端点编号的大小,第二关键字是右端点所在块的编号,第三关键字是所在的修改的时间戳。
- 时间复杂度分析:
假设这个是排完序之后的样子:

那么转移如下:
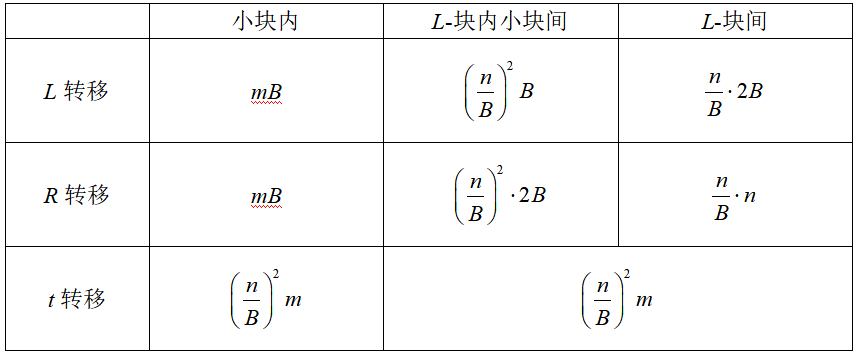
综上所述,时间复杂度的分析如下:
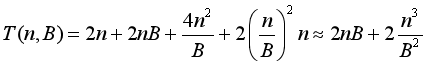
当B取 \(n^{\frac{2}{3}}\)时整体取最小值 - 代码如下:
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define lc p<<1
#define rc p<<1|1
#define int long long
#define vc vector<char>
#define vi vector<int>
#define vvi vector<vector<int>>
#define vpi vector<pair<int,int>>
#define vvc vector<vector<char>>
#define vvpi vector<vector<pair<int,int>>>
typedef long long ll;
typedef tuple<int,int,int> tp;
typedef pair<int,int> PII;
typedef pair<ll,pair<ll,ll>> PIII;
typedef pair<ll,pair<ll,pair<ll,ll>>> pIIII;
const int N = 2e5 + 7;
const int inf = 0x3f3f3f3f;
const int mod = 998244353;
const int none = -1e9 - 1;
int B;
struct query {
int l,r,tim,id;
query(){};
query(int l0,int r0,int tim0,int id0) : l(l0),r(r0),tim(tim0),id(id0) {};
bool operator <(const query &a) const {
if(l/B != a.l/B) return l < a.l;
else if(r/B != a.r/B) return r < a.r;
return tim < a.tim;
}
}Q[N];
void solve() {
int n,m;cin >> n >> m;
vi a(n + 1),color(N*10);
int cntq = 0,cntc = 0,cnt = 0;
vpi change(m + 1);
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
B = pow(n,2.0/3.0);
for(int i = 1; i <= m; i++) {
char ch;cin >> ch;
if(ch == 'Q') {
++cntq;
int l,r;cin >> l >> r;
Q[cntq] = query(l,r,cntc,cntq);
} else {
++cntc;
int p,x;cin >> p >> x;
change[cntc] = {p,x};
}
}
auto add = [&](int x) {
if(color[x] == 0) cnt += 1;
color[x]++;
};
auto del = [&](int x) {
if(color[x] == 1) cnt -= 1;
color[x]--;
};
sort(Q + 1,Q + 1 + cntq);
vi ans(m + 1);
for(int i = 1,l = 1,r = 0,now = 0; i <= cntq; i++) {
int l1 = Q[i].l,r1 = Q[i].r,id = Q[i].id;
while(l > l1) add(a[--l]);
while(r < r1) add(a[++r]);
while(l < l1) del(a[l++]);
while(r > r1) del(a[r--]);
while(now < Q[i].tim) {
int p = change[++now].fi;
if(p >= l && p <= r) del(a[p]),add(change[now].se);
swap(a[p],change[now].se);
}
while(now > Q[i].tim) {
int p = change[now].fi;
if(p >= l && p <= r) del(a[p]),add(change[now].se);
swap(a[p],change[now--].se);
}
ans[id] = cnt;
}
for(int i = 1; i <= cntq; i++) {
cout << ans[i] << "\n";
}
}
signed main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
int t = 1;
//cin >> t;
while(t--) {
solve();
}
//system("pause");
return 0;
}
/*
Do smth instead of nothing and stay organized
Don't get stuck on one approach
*/
树上莫队
- 例题:Count on a tree II
- 算法实现:整个实现原理是和普通莫队时一样的,但是问题是如何将一棵树形结构变成序列结构?我们可以使用欧拉序,那么u到v的路径就可以就可以分两种情况来讨论:
假设lca是u,v的最近公共祖先,fst[i]表示i在欧拉序中第一次出现的时间,lst[i]表示i最后一次在欧拉序中出现的时间
<1>,如果lca是u或者v中的某一个,那么在欧拉序中u,v之间的路径就是fst[u] - fst[v],因为u作为lca,lst[u]肯定在fst[v]之前,所以可以这样表示。其中如果要计算颜色数量的话,那么出现两次的点其实是不在路径里面的,因为出现两次其实就相当于进去然后再出来。
<2>否则的话,假设fst[v] > lst[u],那么lst[u]-fst[v]的这一段序列就是u到v的路径。 - 代码如下:
#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define lc p<<1
#define rc p<<1|1
#define int long long
#define vc vector<char>
#define vi vector<int>
#define vvi vector<vector<int>>
#define vpi vector<pair<int,int>>
#define vvc vector<vector<char>>
#define vvpi vector<vector<pair<int,int>>>
typedef long long ll;
typedef tuple<int,int,int> tp;
typedef pair<int,int> PII;
typedef pair<ll,pair<ll,ll>> PIII;
typedef pair<ll,pair<ll,pair<ll,ll>>> pIIII;
const int N = 5e5 + 7;
const int inf = 0x3f3f3f3f;
const int mod = 998244353;
const int none = -1e9 - 1;
int B;
struct query {
int l,r,id;
int Lca;
query(){}
query(int l0,int r0,int id0) : l(l0),r(r0),id(id0) {
Lca = 0;
}
bool operator < (const query &a)const {
return (l/B == a.l/B ? r < a.r : l < a.l);
}
}q[N];
bool vis[N];
void solve() {
int n,m;cin >> n >> m;
B = sqrt(n*2);
map<int,int> mp;
int cnt = 0;
vi color(n*2 + 100000),fst(n*2 + 100000),lst(n*2 + 100000);
vi father(n*2 + 100000),dep(n*2 + 100000),dfn(n*2 + 100000);
vvi f(n + 1,vi(20));
for(int i = 1; i <= n; i++) {
int t;cin >> t;
if(mp.find(t) == mp.end()) mp[t] = ++cnt;
color[i] = mp[t];
}
vvi g(n + 1,vi());
for(int i = 1; i <= n - 1; i++) {
int u,v;cin >> u >> v;
g[u].push_back(v);
g[v].push_back(u);
}
int tot = 0;
function<void(int,int)> dfs = [&](int u,int fa) -> void {
dep[u] = dep[fa] + 1;
f[u][0] = fa;
dfn[++tot] = u;
fst[u] = tot;
for(int i = 1; i <= 19; i++)
f[u][i] = f[f[u][i - 1]][i - 1];
for(auto v : g[u]) {
if(v == fa) continue;
dfs(v,u);
}
dfn[++tot] = u;
lst[u] = tot;
};
dfs(1,0);
auto lca = [&](int u,int v) -> int {
if(dep[u] < dep[v]) swap(u,v);
for(int i = 19; i >= 0; i--)
if(dep[f[u][i]] >= dep[v])
u = f[u][i];
if(u == v) return v;
for(int i = 19; i >= 0; i--)
if(f[u][i] != f[v][i])
u = f[u][i],v = f[v][i];
return f[u][0];
};
for(int i = 1; i <= m; i++) {
int l,r;cin >> l >> r;
int Lca = lca(l,r);
if(Lca == l || Lca == r) {
if(fst[r] < fst[l]) swap(l,r);
q[i] = query(fst[l],fst[r],i);
} else {
if(lst[r] < fst[l]) swap(l,r);
q[i] = query(lst[l],fst[r],i);
q[i].Lca = Lca;
}
}
sort(q + 1,q + 1 + m);
vi sum(n*2 + 100000),ans(m + 10);
int res = 0;
auto update = [&](int x) {
if(!(vis[x] ^= 1) && (--sum[color[x]]) == 0) res--;
if(vis[x] && (sum[color[x]]++) == 0) res++;
};
for(int i = 1, l = 1,r = 0; i <= m; i++) {
while(l > q[i].l) update(dfn[--l]);
while(r < q[i].r) update(dfn[++r]);
while(l < q[i].l) update(dfn[l++]);
while(r > q[i].r) update(dfn[r--]);
if(q[i].Lca) update(q[i].Lca);
ans[q[i].id] = res;
if(q[i].Lca) update(q[i].Lca);
}
for(int i = 1; i <= m; i++) {
cout << ans[i] << "\n";
}
}
signed main() {
std::ios::sync_with_stdio(0);
std::cin.tie(0);
int t = 1;
//cin >> t;
while(t--) {
solve();
}
//system("pause");
return 0;
}
/*
Do smth instead of nothing and stay organized
Don't get stuck on one approach
*/



