Educational Codeforces Round 27 F. Guards In The Storehouse
Polycarp owns a shop in the capital of Berland. Recently the criminal activity in the capital increased, so Polycarp is thinking about establishing some better security in the storehouse of his shop.
The storehouse can be represented as a matrix with n rows and m columns. Each element of the matrix is either . (an empty space) or x (a wall).
Polycarp wants to hire some guards (possibly zero) to watch for the storehouse. Each guard will be in some cell of matrix and will protect every cell to the right of his own cell and every cell to the bottom of his own cell, until the nearest wall. More formally, if the guard is standing in the cell (x0, y0), then he protects cell (x1, y1) if all these conditions are met:
- (x1, y1) is an empty cell;
- either x0 = x1 and y0 ≤ y1, or x0 ≤ x1 and y0 = y1;
- there are no walls between cells (x0, y0) and (x1, y1). There can be a guard between these cells, guards can look through each other.
Guards can be placed only in empty cells (and can protect only empty cells). The plan of placing the guards is some set of cells where guards will be placed (of course, two plans are different if there exists at least one cell that is included in the first plan, but not included in the second plan, or vice versa). Polycarp calls a plan suitable if there is not more than one empty cell that is not protected.
Polycarp wants to know the number of suitable plans. Since it can be very large, you have to output it modulo 109 + 7.
The first line contains two numbers n and m — the length and the width of the storehouse (1 ≤ n, m ≤ 250, 1 ≤ nm ≤ 250).
Then n lines follow, ith line contains a string consisting of m characters — ith row of the matrix representing the storehouse. Each character is either . or x.
Output the number of suitable plans modulo 109 + 7.
1 3
.x.
3
2 2
xx
xx
1
2 2
..
..
10
3 1
x
.
x
2
In the first example you have to put at least one guard, so there are three possible arrangements: one guard in the cell (1, 1), one guard in the cell (1, 3), and two guards in both these cells.
题意:
在地图上放士兵守卫, " . " 代表那个位置可以放士兵 , " x " 代表那个位置是墙
士兵的守卫范围为:
① 士兵右侧连续的的 " . " 直到墙或者地图边缘
② 士兵下方连续的的 " . " 直到墙或者地图边缘
③ 士兵所处的位置
求 放置士兵使得士兵守卫的不到的位置 <=1 的方案数 (不包括墙)
思路:
由于 1 ≤ nm ≤ 250 所以始终 min ( n,m ) ≤ 15 这是个有用的信息
容易发现 , 放完左上方位置的士兵后左上的情况不会受下面或者右边的影响
因此可以考虑dp
dp [ i ] 表示 按如图编号顺序 从上到下 从左往右 放置第 i 个士兵的局面
状态有两种
1)当前局面已经有一个位置守卫不到
2)当前所有位置都能被守护
但是我们发现一个问题 我们 怎样知道当前位置 放置/不放置 士兵会造成什么影响呢
所以我们需要知道 两个东西
1)上方是否有士兵能守卫到当前位置
2)左侧是否有士兵能守卫到当前位置
这时候对第一点 考虑到状压dp ( 因为min(n,m)<=15 ) 2进制的当前位为 1 则上方有士能守卫到这个位置 为 0 则没有
对第二点考虑增加一维 表示 dp 的状态 1 代表左侧有士能守卫到这个位置 0 则没有
所以 dp方程变成了 4 维 dp [ i ] [ j ] [ k ] [ h ] 表示
放置第 i 个士兵 , j 代表2进制表示上方的状态 , k 代表 是否左侧有士兵能守卫当前位置 0为没有 1为有 , h表示已经被考虑过的位置有多少位置无法被守卫
转移方式如下图
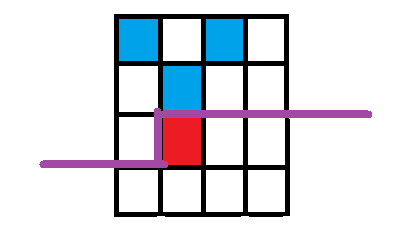
紫色线的左侧和上方为被考虑过的位置 红色为当前位置 蓝色为放置完士兵
那么 图中状态就是
dp [ i ] [ j ] [ k ] [ h ]
i = 9
j = 1110 (二进制) ///分别表示 第一列 第二列 第三列 第四列
k = 0 ( 左侧无士兵 )
h = 0 (没有被守卫到的位置为 0 个)
如果当前位置放置士兵 转移到

dp [ i ] [ j ] [ k ] [ h ]
i = 10
j = 1110 (二进制) ///分别表示 第一列 第二列 第三列 第四列
k = 1 ( 左侧有士兵 )
h = 0 (没有被守卫到的位置为 0 个)
否则转移到
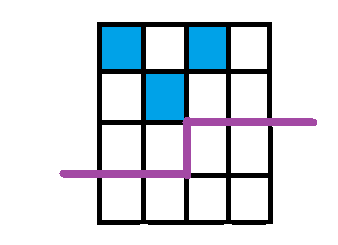
dp [ i ] [ j ] [ k ] [ h ]
i = 10
j = 1110 (二进制) ///分别表示 第一列 第二列 第三列 第四列
k = 0 ( 左侧无士兵 )
h = 0 (没有被守卫到的位置为 0 个)
注意到两点
① 放行末的士兵时 由于要转移到下一行的第一个 那么 他转移时所有状态中的( dp[ i ] [ j ] [ k ] [h ] ) k 只能是 0
② 由于 min (n , m ) <=15 所以当列数比较多时要把 地图行列翻转 使得列数<=15
具体的转移情况稍微看一下就出来了 代码中也有
为了节省空间 转移时可以用滚动数组把dp的第一维降下来
代码:
#include <stdio.h> #include <string.h> #include <ctype.h> #include <stdlib.h> #include <assert.h> #include <math.h> #include <set> #include <map> #include <stack> #include <queue> #include <vector> #include <string> #include <iostream> #include <algorithm> #include <functional> #define mp make_pair #define pb push_back #define mes(a,b) memset(a,b,sizeof(a)) #define mes0(a) memset(a,0,sizeof(a)) #define lson l,mid,pos<<1 #define rson mid+1,r,pos<<1|1 #define rep(i,a,b) for(int i=a;i<=b;i++) #define fi first #define se second #define sss(a) a::iterator #define all(a) a.begin(),a.end() using namespace std; typedef double DB; typedef long long LL; typedef pair<int,int> pii; typedef pair<long long ,int> pli; typedef pair<int,long long > pil; typedef pair<string,int> psi; typedef pair<long long ,long long > pll; const int inf = 0x3f3f3f3f; const long long INF = 0x3f3f3f3f3f3f3f3f; const double pi = acos(-1.0); const int maxn = 100000+10; const int mod = 1e9+7; char MAP[260][260]; int n,m; int dp[2][(1<<15)][2][3]; /// 滚动 , 状压 , 左侧状态, 已填完的是否有空 int main() { dp[0][0][0][0]=1; int op=0; ///滚动 scanf("%d%d",&n,&m); if (m<=n){ for (int i=0;i<n;i++){ scanf("%s",MAP[i]); } }else { for (int i=0;i<n;i++){ getchar(); for (int j=0;j<m;j++){ MAP[j][i]=getchar(); } } swap(n,m); } for (int i=0;i<n;i++){ int j; for (j=0;j<m;j++){ int flag=(j!=m-1); int now=m-j-1; int k; memset(dp[op^1],0,sizeof(dp[op^1])); if (MAP[i][j]=='.'){ for (k=0;k<(1<<m);k++){ ///dp[op][k][w][h]; /// m 1/0 是否填进去 /// 滚动数组, 状压 , 左侧状态, 已填完的是否有空 for (int m=0;m<2;m++){ for (int w=0;w<2;w++){ int st=(k>>now)&1; int S=k|((m|st)<<now); st=(m|w|st)^1; for (int h=0;h<2;h++){ dp[op^1][S][(w|m)&flag][h+st]+=dp[op][k][w][h]; dp[op^1][S][(w|m)&flag][h+st]%=mod; } } } } op^=1; } else { for (k=0;k<(1<<m);k++){ ///dp[op][k][w][h]; /// m 1/0 是否填进去 /// 滚动数组 , 状压 , 左侧状态, 已填完的是否有空 for (int w=0;w<2;w++){ int st=(k>>now)&1; int S=(k^(st<<now)); for (int h=0;h<2;h++){ dp[op^1][S][0][h]+=dp[op][k][w][h]; dp[op^1][S][0][h]%=mod; } } } op^=1; } } } int ans=0; for (int i=0;i<(1<<m);i++){ for (int j=0;j<2;j++){ ans+=dp[op][i][0][j]; ans%=mod; } } cout<<ans<<endl; return 0; }



