1-7、基础开胃菜

文章内容来自王晓华老师

常用技巧

哨兵位
设置哨兵位是程序设计中常用的技巧之一，常用在线性表的处理过程中，比如查找和移动数据操作。哨兵位通常起到两个作用，一个是作为一个临时存储空间使用，另一个是减少不必要的越界判断，简化算法代码复杂度。比如环形链表通常会设置一个表头节点，无论向前或向后遍历，均以这个表头节点为遍历越界（重复）的依据，这样维护链表的时候就不需要专门存储一个表头指针，这个表头节点可以理解为哨兵位。

//带哨兵位的插入排序，ls[0]是哨兵位，数据从 ls[1]开始存放
void insert_sort(int *ls, int n)
{
    for (int i = 2; i <= n; ++i)
    {
        if (ls[i] < ls[i - 1])
        {
            ls[0] = ls[i];//i位置的数存入哨兵位，因为 i 位置会被后面的移动数据操作覆盖
            int j = i;
            while(ls[j - 1] > ls[0])//不用再判断 j 是否越界，直接判断当前位置的值是否大于哨兵位
            {
                ls[j] = ls[j - 1];
                j--;
            }
            ls[j] = ls[0];
        }
    }
}

 

--lua 带哨兵位的插入排序，ls[0]是哨兵位，数据从 ls[1]开始存放
function insert_sort(list, pos)
    for i = 2, pos do
        if(list[i] < list[i-1]) then
            list[0] = list[i]

            local j = i
            while(list[j - 1] > list[0]) do
                list[j] = list[j - 1]
                j = j - 1
            end
            list[j] = list[0]
        end
    end
end

 

巧用数组下标
数组的下标是一个隐含的很有用的属性，巧妙地使用这个属性，对简化算法实现有很大的帮助。比如将阿拉伯数字转换成中文数字的算法，就使用了这种定义中文字符数组：
const char *chnNumChar[CHN_NUM_CHAR_COUNT] = { “零”, “一”, “二”, “三”, “四”, “五”, “六”, “七”, “八”, “九” };

利用数组下标只需一行代码就可找到阿拉伯数字对应的中文数字，比如数字 5 对应的中文数字就是：
const char *chn_five = chnNumChar[5];

 

已知数列由 n 个最大值不超过 32 的正整数组成，请统计一下数列中各个数字出现的次数

int count[33] = { 0 };
    for (int i = 0; i < n; i++)
    {
        count[ numbers[i] ]++;
 }

 

取余的用法
取余运算基本上还是一个除法运算，如果仅仅是判断奇偶数，判断（number & 1）是否等于 0 是更好的方法。更一般的情况，当取余运算的除数是 2 的 n 次方的时候，用 & 运算符代替取余会更高效。比如当 x=2n 的时候，a % x 的结果与 a & (x - 1) 的结果是等价的。（&位操作）

计算机没有环形数据存储方式，只能用线性表模拟，类似这样的模拟环形数据结构中，取余运算也常常用于下标计算。比如用数组模拟环形数组的情况，从任意位置开始遍历数组，当到达数组最后一个元素时，需要回绕的数据的第一个元素继续遍历，可以这样处理：

    int elements[N];

    int pos = x; //遍历起始位置
    for (int i = 0; i < N; i++)
    {
        if (pos < N)
        {
            //使用element[pos]
        }
        else
        {
            pos = 0;//回绕到开始
            //使用element[pos]
        }

        pos++;
    }

 

如果对 pos 位置做取余操作，也可以起到同样的效果，而且循环结构内的代码可以简化：

    for (int i = 0; i < N; i++)
    {
        //使用element[pos]

        pos = (pos + 1) % N;
    }

 

一重循环遍历二维数组
二维表的遍历一般需要两重循环来实现，但是两重循环的代码不如一重循环的代码清爽，很多情况下用一重循环遍历二维表也是一种不错的选择。用一重循环遍历二维表关键是对下标的处理，对于一个 M × N 的二维表，可用以下方法解出对应的二维下标：
int row = i / M
int col = i % M
反过来，也可以用以下公式将二维坐标还原为一维坐标：
int i = row * M + col
很多九宫格类型的游戏棋盘的初始化就是用的这种方法。

for(int i = 0; i < 9; i++)
{
　　int row = i / 3;
　　int col = i % 3;
　　game->cells[row][col].fixed = false;
}

 

棋盘（迷宫）类算法方向遍历
二维棋盘和迷宫的搜索常常是沿着与某个位置相临的 4 个或 8 个方向展开，对这些方向的遍历就是搜索算法的主要结构

如果从 i 行 j 列开始向上、下、左、右四个方向搜索，则这四个方向可转换为以下行、列坐标关系：
• 向左搜索：行坐标 i 不变，列坐标 j-1
• 向上搜索：行坐标 i-1，列坐标不变
• 向右搜索：行坐标 i 不变，列坐标 j+1
• 向下搜索：行坐标 i+1，列坐标不变
根据以上关系，首先定义二维数组下标偏移量，然后定义一个偏移量数组，分别表示向四个方向的数组下标偏移量：

typedef struct 
{
int x_off;
int y_off;
}OFFSET;

OFFSET dir_offset[] = {{0,-1},{-1,0},{0,1},{1,0}};

 

假设当前位置的二维数组下标是 x、y，则对此位置开始向四个方向搜索的代码可以如此实现：

for(int i = 0; i < count_of(dir_offset); i++)
{
int new_x = x + dir_offset[i].x_off;
int new_y = y + dir_offset[i].y_off;
……
}

这种算法实现避免了对每个方向都进行下标计算，即便是增加两个斜线方向，从 4 个方向搜索扩展到 8 个方向搜索，只需调整dir_offset数组即可，摆脱了冗长的 switch-case 代码结构。

 

单链表
单链表有很多有意思的问题，比如“判断单链表是否有环”、“如何一次遍历就找到链表中间位置节点”、“单链表中倒数第 k 个节点”等问题，解决这三个问题需要使用双指针的技巧，

比如第一个问题，设置一个“慢指针”和一个“快指针”，从链表头开始遍历，慢指针一次向后移动一个节点，快指针一次移动两个节点。如果链表没有环，则快指针会先到达最后一个节点（NULL），否则的话，快指针会追上慢指针（相遇）。

第二个问题同样设置一快一慢两个指针，慢指针一次移动一个节点，快指针一次移动两个节点，当快指针移动到结尾时，慢指针指向的就是中间节点。

第三个问题也是双指针，其中一个先移动 k 个节点，然后两个指针以相同的速度一起移动，当先移动的指针移动到结尾的时候，后移动的指针指向的就是倒数第 k 个节点。

单链表逆序

 

 

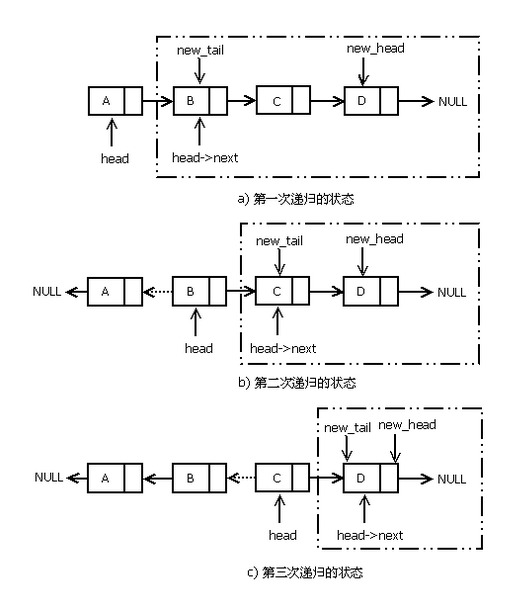
递归方法的核心就是确定递归子问题，链表类的问题找递归子问题的方法基本固定，就是每次除去链表头部第一个节点，剩下的序列作为分解的子问题。

主要的算法实现思路是先将当前的表头节点从链表中拆出来，然后对剩余的节点组成的子链表进行逆序，最后将当前的表头节点连接到新链表的尾部。

如图（2）所示，每一轮递归都是先对子链表逆序，然后将拆出来的 head 节点附加到新的子链表的尾部。虽然递归调用的顺序是从 a 到 c 的顺序，但是递归逆序的实际操作过程需要从 c 到 a 反着来理解。

图（2-c）就是递归符合退出条件时的状态，此时子链表只剩一个节点，直接返回这个节点作为子链表的 new_head 节点。随后的递归操作将子链表的 head 节点附加到new_head节点的尾部，如代码所示：

LINK_NODE *reverse_link(LINK_NODE *head)
{
    LINK_NODE *newHead;

    if ((head == nullptr) || (head->next == nullptr))
        return head;

    newHead = reverse_link(head->next); /*递归逆转子链表部分*/
    head->next->next = head; /*回朔部分*/
    head->next = nullptr;

    return newHead;
}

-- lua
function reverse_link(head)
    local newHead
    if(not head or not head.next) then
        return head
    end

    newHead = reverse_link(head.next)

    head.next.next = head
    head.next = nil

    return newHead
end

这段代码的关键点是头节点 head 的下一个节点 head→next 将是逆序后的新链表的尾节点，也就是说，被摘除的头接点 head 需要被链接到 head→next 才能完成整个链表的逆序。

 

利用英文字母的 ASCII 编码特点
ASCII 表中 26 个英文字母是连续的，小写字母 a-z 对应的 ASCII 码值是 0x61-0x7A，大写字母 A-Z 对应的 ASCII 码值是 0x41-0x5A。如果将字母'A'以整数看待，它就是 0x41，同样，将整数 0x41 当作字符看待，它就是字母'A'。
判断一个 char 是大写英文字母还是小写英文字母，就可以利用这种连续的特点，直接做范围判断：

ASCII 码表中小写字母和对应的大写字母之间的 ASCII 码值相差 0x20，可以利用这个特点进行大小写的转换，小写字母减 0x20 可以得到对应的大写字母，大写字母加上 0x20 可以得到对应的小写字母

 

常见问题

数组链表
数组的特点是存储空间固定，数据存取高效，但是缺点是数据插入和删除需要移动数组元素，不适合插入和删除比较频繁的场合。

链表的特点恰恰是插入和删除比较高效，但是缺点是需要动态申请存储空间，在一些系统上，内存申请和释放的开销比较大，使用链表存在性能问题。

如果存储的数据元素的个数是固定或总数是受限的，可以考虑用数组链表这种存储方式。数组链表的存储空间是数组，但是每个元素的指针域存放的不是指针，而是链接元素对应的数组下标，依靠数组下标形成链式关系。

用数组存储二叉树
根据二叉树的特点，二叉树父子节点的数组下标关系有以下规律：
• 父节点 i 的左子节点是 2∗i+12∗i+1
• 父节点 i 的右子节点是 2∗i+22∗i+2
• 子节点 i 的父节点是 ⌊(i−1)/2⌋

//先序遍历数组存储的二叉树
void pre_order(char array_tree[], int root)
{
　　if ((root >= MAX_TREE_NODE) || (array_tree[root] == -1))
　　{
　　　　return;
　　}

　　std::cout << array_tree[root];
　　pre_order(array_tree, 2 * root + 1);
　　pre_order(array_tree, 2 * root + 2);
}

 

-- lua
function order(tree_list, root)
    if(root >= #tree_list or tree_list[root] == -1) then
        return
    end

    print("==========root", tree_list[root])
    order(tree_list, 2 * root + 1)
    order(tree_list, 2 * root + 2)
end

 

topN 问题和最小堆
从大量的数据中找出符合条件的 n 个数据就是所谓的 topN 问题，

常见的问题比如：从 N 个无序的数中找出最小的前 k 个数（或最大的前 k 个数）。

对这种问题，如果 N 的规模不大，可以考虑先对 N 个数进行升序排序（或降序排序），然后输出前 k 个数。排序算法的时间复杂度最好就是 O(nlg(n))，这个方法基本上也是 O(nlg(n)) 的时间复杂度。但是当 N 的规模大到一定程度时，完整的对 N 个数进行排序仍然是个很大的开销，在这种情况下，通常采用的方法是用一个小的有序数据结构维护前 k 个被选出来的最小数，依次遍历 N 个数，如果某个数比选出来的前 K 个数中最大的那个数小，则将这个数插入到这个小的有序数据结构中，同时淘汰掉最大的那个数。当 N 个数都处理完，这个有序数据结构中的 k 个数就是最小的前 k 个数。这个方法的主要处理就是维护前 k 个有序的数需要的比较操作，有序表的比较操作次数是 lg(k) 次，因此这个方法的时间复杂度是 O(nlg(k))。一般情况下，k 都是远远小于 N 的，因此这种方法大大优于直接排序的方法。

常用的 hash 算法（字符串比较）

常用设计原则与策略

程序设计的一致性原则

以空间换时间的策略
　　预先准备好这些结果，避免每次都计算