JS-10种排序算法整理

参考文章  https://www.cnblogs.com/beli/p/6297741.html

排序算法说明:

（1）对于评述算法优劣术语的说明

稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面；
不稳定：如果a原本在b的前面，而a=b，排序之后a可能会出现在b的后面；

内排序：所有排序操作都在内存中完成；
外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；

时间复杂度: 一个算法执行所耗费的时间。
空间复杂度: 运行完一个程序所需内存的大小。

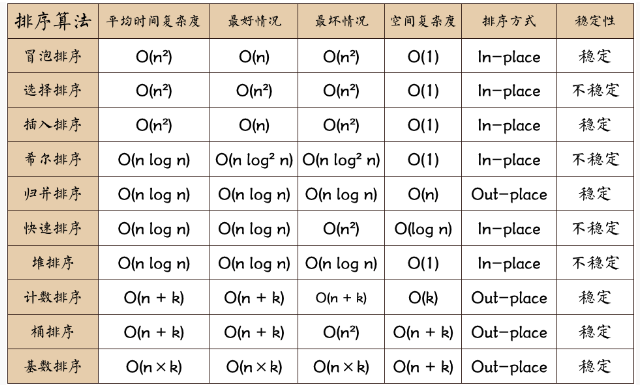
(2)排序算法图片总结:

　　

 

1.冒泡排序

　　解析：1.比较相邻的两个元素，如果前一个比后一个大，则交换位置。

　　　　　2.第一轮的时候最后一个元素应该是最大的一个。

　　　　　3.按照步骤一的方法进行相邻两个元素的比较，这个时候由于最后一个元素已经是最大的了，所以最后一个元素不用比较。

　　

function sort(elements){
    for (let i = 0; i < elements.length - 1; i++){
        for(let j = 0; j < elements.length - 1 - i; j++){
            if(elements[j] < elements[j + 1]){
                let temp = elements[j];
                elements[j] = elements[j + 1];
                elements[j + 1] = temp;
            }
        }
    }
}

 

2.快速排序

解析：快速排序是对冒泡排序的一种改进，第一趟排序时将数据分成两部分，一部分比另一部分的所有数据都要小。然后递归调用，在两边都实行快速排序。

function quickSort(elements){
    if (elements.length <= 1 ){
        return elements;
    }
    var mid = Math.floor(elements.length / 2);
    var val = elements[mid];

    var left = [];
    var right = [];
    for (let i = 0; i <elements.length; i++){
        if (elements[i] > val){
            right.push(elements[i]);
        }else if(element[i] < val){
            left.push(elements[i]);
        }
    }
    // concat() 方法用于连接两个或多个数组。此方法返回一个新数组，不改变原来的数组。
    // arrayObject.concat(array1,array2,...,arrayN)
    return quickSort(left).conact([val], quickSort(right));
}

 

3.插入排序

解析：

 （1） 从第一个元素开始，该元素可以认为已经被排序

 （2） 取出下一个元素，在已经排序的元素序列中从后向前扫描

 （3） 如果该元素（已排序）大于新元素，将该元素移到下一位置

 （4） 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置

 （5）将新元素插入到下一位置中

 （6） 重复步骤2

理解：

　　数组分成已排序和未排序，从第0个开始，第0个认为是已排序

　　取第i个，那么从i - 1遍历到0，不停的和前一个元素交换位置，直到找到第一个val比i的值小或者等于的位置，插入在他之后

function insertSort(element){
    for (let i = 0; i < element.length; i++){
        // 如果i的值比i-1大，那就不需要排序了
        if (element[i] < element[i - 1]){
            let startJ = i - 1;
            let keyVal = element[i];

            //由于keyVal小于element[startJ]，那么把关键字element[startJ]往后移动一个位置
            while (startJ >= 0 && keyVal < element[startJ]){
                element[startJ + 1] = element[startJ];
                startJ--;
            }
            element[startJ + 1] = keyVal;
        }
    }
}

 

4.选择排序

解析:

　　首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

　　以此类推，直到所有元素均排序完毕。

function selectionSort(elements){
    var minIndex = 0;
    for (let i = 0; i < elements.length - 1; i++){
        minIndex = i;
        for(let j = i + 1; j < elements.length; j++){
            if (elements[minIndex] > elements[j]){
                minIndex = j;
            }
        }

        var temp = elements[i];
        elements[i] = elements[minIndex];
        elements[minIndex] = temp;
    }
    return elements;
}

 

5.希尔排序（这个没有自己实现）

解析:

　　先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序

理解：

　　缩小增量排序

　　先以固定间隔a将数组分成 len / a组，然后对每组进行直接插入排序，直到间隔为1进行最后一趟排序

 

6.归并排序

解析:

　　归并排序是一种稳定的排序方法。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

　　参考链接 https://www.cnblogs.com/zichi/p/4796727.html

// 归并排序
function mergeSort(arr){ // 自上而下的递归方法
    var len = arr.length;
    if(len < 2){
        return arr;
    }

    var middle = Math.floor(len / 2);
    var left = arr.slice(0, middle); // arrayObject.slice(start,end) 方法可从已有的数组中返回选定的元素。返回一个新的数组，包含从 start 到 end （不包括该元素）的 arrayObject 中的元素
    var right = arr.slice(middle);
    return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right){
    var result = [];

    while(left.length && right.length){
        if(left[0] <= right[0]){
            result.push(left.shift());
        }else{
            result.push(right.shift());
        }
    }

    while(left.length){
        result.push(left.shift());
    }
    while(right.length){
        right.push(left.shift());
    }
    return result;
}

// 迭代实现 解决栈溢出错误的方案
function merge(left, right) {
    var result = [];
  
    while (left.length && right.length) {
      if (left[0] < right[0])
        result.push(left.shift());
      else
        result.push(right.shift());
    }
  
    return result.concat(left, right);
  }
  
  function mergeSort(a) {
    if (a.length === 1)
      return a;
  
    var work = [];
    for (var i = 0, len = a.length; i < len; i++)
      work.push([a[i]]);
  
    work.push([]); // 如果数组长度为奇数
  
    for (var lim = len; lim > 1; lim = ~~((lim + 1) / 2)) {
      for (var j = 0, k = 0; k < lim; j++, k += 2) 
        work[j] = merge(work[k], work[k + 1]);
  
      work[j] = []; // 如果数组长度为奇数
    }
  
    return work[0];
  }
  
  console.log(mergeSort([1, 3, 4, 2, 5, 0, 8, 10, 4]));

 

7.堆排序

解析:

　　堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

// 堆
//对于给定的某个结点的下标 i，可以很容易的计算出这个结点的父结点、孩子结点的下标：
// Parent(i) = floor(i/2)，i 的父节点下标
// Left(i) = 2i，i 的左子节点下标
// Right(i) = 2i + 1，i 的右子节点下标

// 堆排序
// 堆排序就是把最大堆堆顶的最大数取出，将剩余的堆继续调整为最大堆，再次将堆顶的最大数取出，这个过程持续到剩余数只有一个时结束。在堆中定义以下几种操作：
// 最大堆调整（Max-Heapify）：将堆的末端子节点作调整，使得子节点永远小于父节点
// 创建最大堆（Build-Max-Heap）：将堆所有数据重新排序，使其成为最大堆
// 堆排序（Heap-Sort）：移除位在第一个数据的根节点，并做最大堆调整的递归运算
function heapSort(array){
    function swap(array, i, j){ // 交换位置
        var temp = array[i];
        array[i] = array[j];
        array[j] = temp;
    }

    /**
     * 从 index 开始检查并保持最大堆性质
     *
     * @array
     *
     * @index 检查的起始下标
     *
     * @heapSize 堆大小
     *
     **/
    function maxHeapify(array, index, heapSize){
        var iMax, iLeft, iRight;

        while(true){
            iMax = index;
            iLeft = 2 * index + 1;
            iRight = 2 * (index + 1);

            if(iLeft < heapSize && array[index] < array[iLeft]){
                iMax = iLeft;
            }
            if(iRight < heapSize && array[index] < array[iRight]){
                iMax = iRight;
            }

            if(iMax != index){
                swap(array, iMax, index);
                index = iMax;
            }else{
                break;
            }
        }
    }

    function buildMaxHeap(array){
        var i;
        var iParent = Math.floor(array.length / 2) - 1;

        for(let i = iParent; i >= 0; i--){
            maxHeapify(array, i, array.length);
        }
    }

    // 先调用Build-Max-Heap将数组改造为最大堆
    // 由于堆顶元素必然是堆中最大的元素，堆顶和堆底元素交换，操作之后，堆中存在的最大元素被分离出堆
    // 重复n-1次之后，数组排列完毕
    function sort(array){
        buildMaxHeap(array, heapSize);

        for(let i = array.length - 1; i > 0; i--){
            swap(array, 0, i);
            maxHeapify(array, 0, i);
        }
        return array;
    }

    return sort(array);
}

 

8.计数排序

 解析:

　　计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。

// 1.查找待排序数组中最大和最小的元素
// 2.统计每个值为i的元素的出现次数
// 3.对所有计数开始累加(从min开始,每一项和前一项相加)
// 4.反向填充目标数组,将每个元素i放在新数组的第C[i]项,每放一个元素,计数-1.

function countingSort(array){
    var len = array.length;
    var B = [];
    var C = [];
    var min =  max = array[0];

    for (let i = 0; i < len; i ++){
        min = array[i] < min ? array[i] : min;
        max = array[i] > max ? array[i] : max;

        C[array[i]] = (C[array[i]] || 0) + 1;
    }

    // 第一种思路 先求和，得出的是array[i]占用的区间 上个元素值 ~ 当前元素值，然后遍历array找位置（正序或者倒序都可？）
    for (let i = min; i < max; i++){
        C[i + 1] = (C[i] || 0) + (C[i + 1] || 0);
    }
    // 数组从0开始 所以放置的位置是C[array[i]] - 1
    for(let i = len; i > 0; i--){
        B[C[array[i]] - 1] = array[i];
        C[array[i]]--; // 这里是为了重复的元素找位置
    }
    // 第二种思路 更简单易懂 但是效率低
    for (let i = min; i < max; i++){
        if (C[i]){
            for(let j = 0; i < C[i]; j++){
                B.push(i);
            }
        }
    }

    return B;
}

 

9.桶排序

解析:

　　假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排

　　

// 操作步骤说明：
// （1）设置桶的数量为5个空桶，找到最大值110，最小值7，每个桶的范围20.8=(110-7+1)/5 。
// （2）遍历原始数据，以链表结构，放到对应的桶中。数字7，桶索引值为0，计算公式为floor((7 – 7) / 20.8)， 数字36，桶索引值为1，计算公式floor((36 – 7) / 20.8)。
// （3）当向同一个索引的桶，第二次插入数据时，判断桶中已存在的数字与新插入数字的大小，按照左到右，从小到大的顺序插入。如：索引为2的桶，在插入63时，桶中已存在4个数字56，59，60，65，则数字63，插入到65的左边。
// （4）合并非空的桶，按从左到右的顺序合并0，1，2，3，4桶。
// （5）得到桶排序的结构

function bucketSort(array, num){ // num为设置的桶的数量
    if (array.length <= 1){
        return array;
    }

    var len = array.length;
    var buckets = [];
    var result = [];
    var space = 0;
    var min = max = array[0];
    var regex = '/^[1-9]+[0-9]*$/';
    var re = new RegExp(regex);

    num = num || ((num > 1 && re.test(num)) ? num : 10);
    
    // 找到最大、最小值
    for(let i = 0; i < len; i++){
        max = array[i] > max ? array[i] : max;
        min = array[i] < min ? array[i] : min;
    }
    // 设定桶的容量
    space = (max - min + 1) / num;

    for(let i = 0; i < len; i++){
        // array[i]根据val去找放在哪个桶 index = floor((val – min) / space)
        var index = Math.floor((array[i] - min) / space);
        if(buckets[index]){ // 非空桶 倒着找位置
            var k = buckets.length - 1;
            while(k >= 0 && buckets[index][k] > array[i]){
                buckets[index][k + 1] = buckets[index][k];
                k--;
            }

            // 找到一个小于等于array[i]的位置k，插入其后
            buckets[index][k + 1] = array[i];
        }else{ //空桶 初始化
            buckets[index] = [];
            buckets[index].push(array[i]);
        }
    }

    var n = 0;
    while(n < num){
        result = result.concat(buckets[n]);
        n ++;
    }
    return result;
}

 

10. 基数排序

解析:

　　基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优

　　先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以是稳定的。

/**
 * 类似我们比较大小时先比较个位 再比较百位的思想
 * 基数排序适用于：
 * (1)数据范围较小，建议在小于1000
 * (2)每个数值都要大于等于0
 * @author damonare
 * @param arr 待排序数组
 * @param maxDigit 最大位数
*/
function radixSort(arr, maxDigit){
    var mod = 10;
    var dev = 1;
    var counter = [];

    // 第一趟比个位  第二趟十位 以此类推
    for(var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10){
        for (var j = 0; j < arr.length; j++){
            var index = parseInt((arr[j] % mod) / dev);
            if (counter[index] == null){
                counter[index] = [];
            }
            counter[index].push(arr[j]);
        }

        var pos = 0;
        for (let j = 0; j < counter.length; j++){
            var value = null;
            if(counter[j] != null){
                value = counter[j].shift();
                while(value != null){
                    arr[pos] = value;
                    pos++;
                    value = counter[j].shift();
                }
            }
        }
    }
    return arr;
}

 

基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

基数排序：根据键值的每位数字来分配桶 计数排序：每个桶只存储单一键值 桶排序：每个桶存储一定范围的数值

 

对于基本排序算法，需要理解其原理，能用代码实现，并且能够知道对应的时间复杂度和空间复杂度，能够在不同的场景选用合适的算法