二叉树--堆的实现(数组,非指针)
堆的重要性质就是 儿子的值一定不小于父亲的值
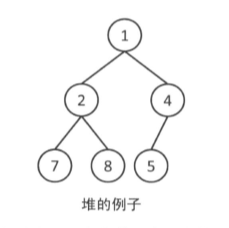
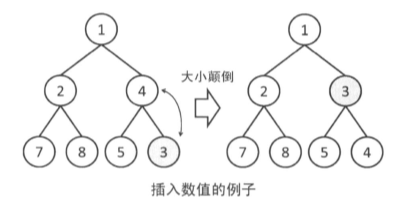
向堆中插入数值时,首先在堆的末尾插入该数值,然后不断向上提升知道没有大小颠倒为止。
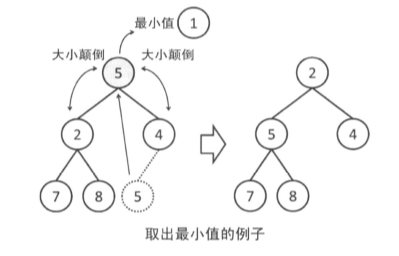
从堆中删除最小值时,首先把堆的最后一个节点的数值复制到根节点上,并且删除最后一个节点。然后不断向下交换直到没有大小颠倒为止。在向下交换的过程中,如果有2个儿子,那么选择数值较小的儿子(如果儿子比自己小的话)进行交换。
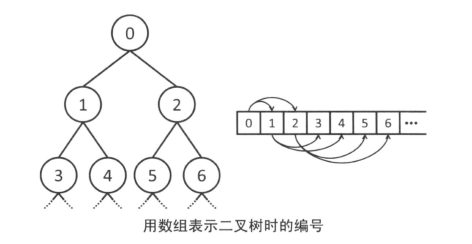
用数组表示二叉树时的编号
const int maxn=1e5+5;
int heap[maxn],sz;
void push(int x)
{
int i=sz++;//自己节点的编号
while(i>0)
{
int p=(i-1)/2;//父亲节点的编号
if(heap[p]<=x)//如果已经没有大小颠倒则退出
break;
heap[i]=heap[p];//把父亲节点的数值放下来,把自己提上去
i=p;
}
heap[i]=x;
}
int pop()
{
int ret=heap[0];//根节点即最小值
int x=heap[--sz];//要提到根的数值
int i=0;//从根开始向下交换
while(i*2+1<sz)
{
int lson=i*2+1,rson=i*2+2;
if(rson<sz&&heap[rson]<heap[lson])//比较儿子的值
lson=rson;
if(heap[lson]>=x)//已经没有大小颠倒则退出
break;
heap[i]=heap[lson];//把儿子的数值提上来
i=lson;
}
heap[i]=x;
return ret;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号