素数的快速筛选（埃氏筛法）

　　要枚举n以内的素数，可以用埃氏筛法。这是一个与辗转相除法一样古老的算法。

 

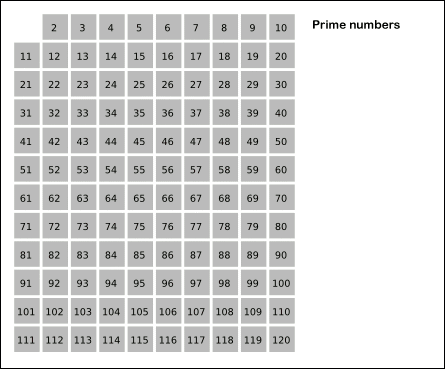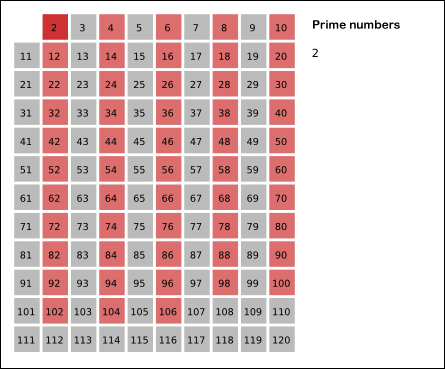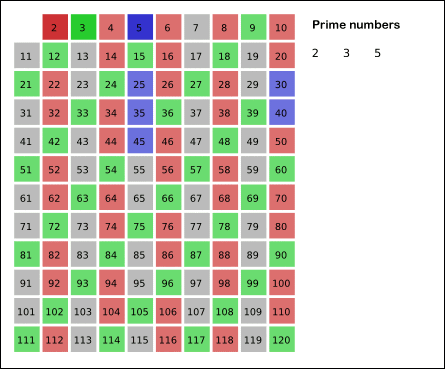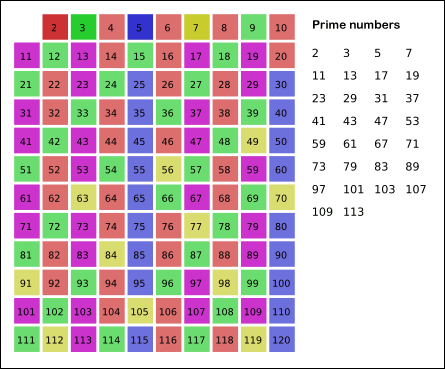
首先，将2到n范围内的所有整数写下来。其中最小的数字2是素数。将表中所有2的倍数都划去。表中剩余的最小数字是3，它不能被更小的数整除，所以是素数。再将表中所有3的倍数全都划去。依次类推，如果表中剩余的最小数字是m时，m就是素数。然后将表中所有m的倍数全部划去。像这样反复操作，就能依次枚举n以内的素数。

 

int prime[maxn];//第i个素数
bool is_prime[maxn];//is_prime[i]为true表示i是素数
int sieve(int n)//返回n以内的素数
{
    int cnt=0;
    for(int i=0;i<=n;i++)
        is_prime[i]=true;
    is_prime[0]=is_prime[1]=false;
    for(int i=2;i<=n;i++)
        if(is_prime[i])
        {
            prime[cnt++]=i;
            for(int j=2*i;j<=n;j+=i)
                is_prime[j]=false;
        }
    return cnt;
}

埃氏筛的复杂度仅有O（nloglogn），算是比较快的了。当数据量不是太大的时候，可以把它的复杂度看作是线性的。

最近在学Python，附上Python 3.6的代码：

def eratosthenes(n):
    P = [i for i in range(2, n+1)]
    p = 0
    while True:
        for i in P[p + 1:]:
            if i % P[p] == 0:
                P.remove(i)
        if P[p]**2 >= P[-1]:
            break
        p += 1
    return P

if __name__ == "__main__":
    print (eratosthenes(120))