Pytorch：单卡多进程并行训练
在深度学习的项目中，我们进行单机多进程编程时一般不直接使用multiprocessing模块，而是使用其替代品torch.multiprocessing模块。它支持完全相同的操作，但对其进行了扩展。Python的multiprocessing模块可使用fork、spawn、forkserver三种方法来创建进程。但有一点需要注意的是，CUDA运行时不支持使用fork，我们可以使用spawn或forkserver方法来创建子进程，以在子进程中使用CUDA。
算法的完整实现代码我已经上传到了GitHub仓库：Distributed-ML-PySpark（包括其它分布式机器学习算法），感兴趣的童鞋可以前往查看。
1 导引
我们在博客《Python：多进程并行编程与进程池》中介绍了如何使用Python的multiprocessing模块进行并行编程。不过在深度学习的项目中，我们进行单机多进程编程时一般不直接使用multiprocessing模块，而是使用其替代品torch.multiprocessing模块。它支持完全相同的操作，但对其进行了扩展。
Python的multiprocessing模块可使用fork、spawn、forkserver三种方法来创建进程。但有一点需要注意的是，CUDA运行时不支持使用fork，我们可以使用spawn或forkserver方法来创建子进程，以在子进程中使用CUDA。创建进程的方法可用multiprocessing.set_start_method(...) API来进行设置，比如下列代码就表示用spawn方法创建进程：
import torch.multiprocessing as mp
mp.set_start_method('spawn', force=True)
事实上，torch.multiprocessing在单机多进程编程中应用广泛。尤其是在我们跑联邦学习实验时，常常需要在一张卡上并行训练多个模型。注意，Pytorch多机分布式模块torch.distributed在单机上仍然需要手动fork进程。本文关注单卡多进程模型。
2 单卡多进程编程模型
我们在上一篇文章中提到过，多进程并行编程中最关键的一点就是进程间通信。Python的multiprocessing采用共享内存进行进程间通信。在我们的单卡多进程模型中，共享内存实际上可以直接由我们的CUDA内存担任。
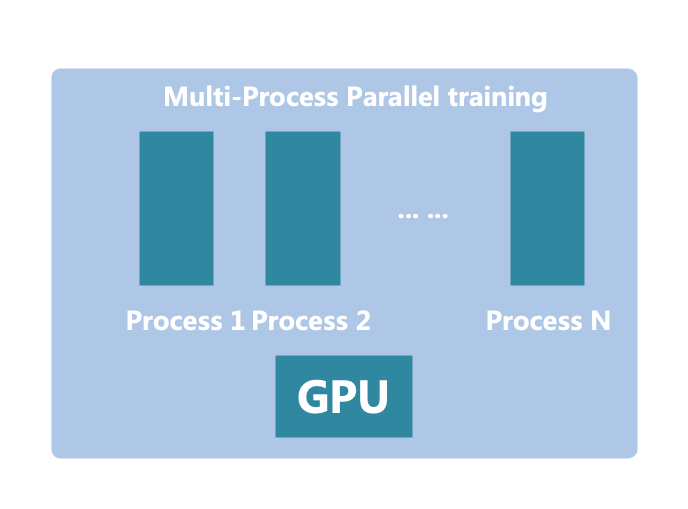
可能有读者会表示不对啊，Pytorch中每个张量有一个tensor.share_memory_()用于将张量的数据移动到主机的共享内存中呀，如果CUDA内存直接担任共享内存的作用，那要这个API干啥呢？实际上，tensor.share_memory_()只在CPU模式下有使用的必要，如果张量分配在了CUDA上，这个函数实际上为空操作（no-op）。此外还需要注意，我们这里的共享内存是进程间通信的概念，注意与CUDA kernel层面的共享内存相区分。
注意，Python/Pytorch多进程模块的进程函数的参数和返回值必须兼容于
pickle编码，任务的执行是在单独的解释器中完成的，进行进程间通信时需要在不同的解释器之间交换数据，此时必须要进行序列化处理。在机器学习中常使用的稀疏矩阵不能序列化，如果涉及稀疏矩阵的操作会发生异常:NotImplementedErrorCannot access storage of SparseTensorImpl，在多进程编程时需要转换为稠密矩阵处理。
3 实例： 同步并行SGD算法
我们的示例采用在博客《分布式机器学习：同步并行SGD算法的实现与复杂度分析（PySpark）》中所介绍的同步并行SGD算法。计算模式采用数据并行方式，即将数据进行划分并分配到多个工作节点(Worker)上进行训练。同步SGD算法的伪代码描述如下：
注意，我们此处的多进程共享内存，是无需划分数据而各进程直接对共享内存进行异步无锁读写的（参考Hogwild！算法[3]）。但是我们这里为了演示同步并行SGD算法，还是为每个进程设置本地数据集和本地权重，且每个epoch各进程进行一次全局同步，这样也便于我们扩展到同步联邦学习实验环境。
在代码实现上，我们需要先对本地数据集进行划，这里需要继承torch.utils.data.subset以自定义数据集类（参见我的博客《Pytorch：自定义Subset/Dataset类完成数据集拆分 》）：
class CustomSubset(Subset):
'''A custom subset class with customizable data transformation'''
def __init__(self, dataset, indices, subset_transform=None):
super().__init__(dataset, indices)
self.subset_transform = subset_transform
def __getitem__(self, idx):
x, y = self.dataset[self.indices[idx]]
if self.subset_transform:
x = self.subset_transform(x)
return x, y
def __len__(self):
return len(self.indices)
def dataset_split(dataset, n_workers):
n_samples = len(dataset)
n_sample_per_workers = n_samples // n_workers
local_datasets = []
for w_id in range(n_workers):
if w_id < n_workers - 1:
local_datasets.append(CustomSubset(dataset, range(w_id * n_sample_per_workers, (w_id + 1) * n_sample_per_workers)))
else:
local_datasets.append(CustomSubset(dataset, range(w_id * n_sample_per_workers, n_samples)))
return local_datasets
local_train_datasets = dataset_split(train_dataset, n_workers)
然后定义本地模型、全局模型和本地权重、全局权重：
local_models = [Net().to(device) for i in range(n_workers)]
global_model = Net().to(device)
local_Ws = [{key: value for key, value in local_models[i].named_parameters()} for i in range(n_workers)]
global_W = {key: value for key, value in global_model.named_parameters()}
然后由于是同步算法，我们需要初始化多进程同步屏障：
from torch.multiprocessing import Barrier
synchronizer = Barrier(n_workers)
训练算法流程（含测试部分）描述如下：
for epoch in range(epochs):
for rank in range(n_workers):
# pull down global model to local
pull_down(global_W, local_Ws, n_workers)
processes = []
for rank in range(n_workers):
p = mp.Process(target=train_epoch, args=(epoch, rank, local_models[rank], device,
local_train_datasets[rank], synchronizer, kwargs))
# We first train the model across `num_processes` processes
p.start()
processes.append(p)
for p in processes:
p.join()
aggregate(global_W, local_Ws, n_workers)
# We test the model each epoch
test(epoch, global_model, device, test_dataset, kwargs)
其中的pull_down()函数负责将全局模型赋给本地模型：
def pull_down(global_W, local_Ws, n_workers):
# pull down global model to local
for rank in range(n_workers):
for name, value in local_Ws[rank].items():
local_Ws[rank][name].data = global_W[name].data.clone()
aggregate()函数负责对本地模型进行聚合（这里我们采用最简单的平均聚合方式）：
def aggregate(global_W, local_Ws, n_workers):
# init the global model
for name, value in global_W.items():
global_W[name].data = torch.zeros_like(value)
for rank in range(n_workers):
for name, value in local_Ws[rank].items():
global_W[name].data += value.data
for name in local_Ws[rank].keys():
global_W[name].data /= n_workers
最后，train_epoch和test_epoch定义如下(注意train_epoch函数的结尾需要加上 synchronizer.wait()表示进程间同步)：
def train_epoch(epoch, rank, local_model, device, dataset, synchronizer, dataloader_kwargs):
torch.manual_seed(seed + rank)
train_loader = torch.utils.data.DataLoader(dataset, **dataloader_kwargs)
optimizer = optim.SGD(local_model.parameters(), lr=lr, momentum=momentum)
local_model.train()
pid = os.getpid()
for batch_idx, (data, target) in enumerate(train_loader):
optimizer.zero_grad()
output = local_model(data.to(device))
loss = F.nll_loss(output, target.to(device))
loss.backward()
optimizer.step()
if batch_idx % log_interval == 0:
print('{}\tTrain Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
pid, epoch + 1, batch_idx * len(data), len(train_loader.dataset),
1. * batch_idx / len(train_loader), loss.item()))
synchronizer.wait()
def test(epoch, model, device, dataset, dataloader_kwargs):
torch.manual_seed(seed)
test_loader = torch.utils.data.DataLoader(dataset, **dataloader_kwargs)
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
output = model(data.to(device))
test_loss += F.nll_loss(output, target.to(device), reduction='sum').item() # sum up batch loss
pred = output.max(1)[1] # get the index of the max log-probability
correct += pred.eq(target.to(device)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest Epoch: {} Global loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
epoch + 1, test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
我们在epochs=3、n_workers=4的设置下运行结果如下图所示(我们这里仅展示每个epoch同步通信后，使用测试集对全局模型进行测试的结果)：
Test Epoch: 1 Global loss: 0.5926, Accuracy: 8676/10000 (87%)
Test Epoch: 2 Global loss: 0.3062, Accuracy: 9165/10000 (92%)
Test Epoch: 3 Global loss: 0.2283, Accuracy: 9321/10000 (93%)
可以看到测试结果是趋于收敛的。
参考
- [1] Pytorch: multiprocessing
- [2] Pytorch: What is the shared memory?
- [3] Recht B, Re C, Wright S, et al. Hogwild!: A lock-free approach to parallelizing stochastic gradient descent[J]. Advances in neural information processing systems, 2011, 24.
