堆排序

堆排序

概述

堆排序（这里指从小到大）巧妙地运用了大顶堆（一种每个根节点都大于其两个子节点的特殊二叉树）的性质对数组进行排序，时间复杂度为O（NlogN）。不仅在排序之前要构建大顶堆，而且每轮交换都要重新下沉堆顶元素以维护大顶堆，显得不是很方便。但是因为这个方法设计巧妙，直观而容易理解，我们还是要学习她。

算法讲解

1.首先，待排序的数组初始如下，可以看成一个普通的二叉树。
（注意：这里的数组下标从0开始，后面的下标运算都是针对下标从0开始的数组而言的，因为从下标开始的数组下表之间的关系又有不同）

2.之后，从最后一个根节点（即下标为array.length/2-1的点,这里是大小为6的节点开始向上遍历所有根节点，并同时将不满足最大值条件的根节点与其子节点交换，以构建大顶堆

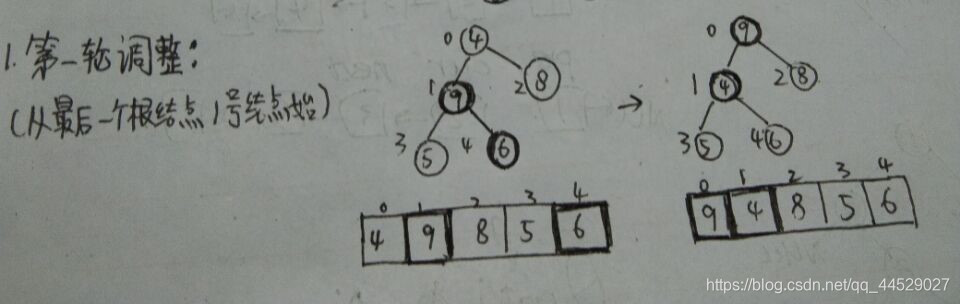
注意：重点来了，我们已经把大小为4的节点和大小为9的节点进行了交换，但是交换下去的大小为4的节点管不住大小为5、6的节点，怎么办？

继续将4节点递归地往下调整即可：

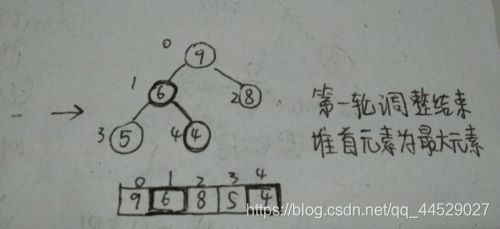
当递归走向出口。也就是第一轮调整结束时，堆顶元素已经是当前堆的最大元素了
3.于是，我们接着将堆顶元素与堆尾元素交换即可

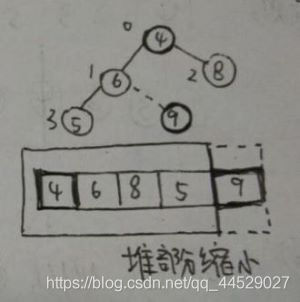
注意:交换之后的元素9属于排序好的数组，不再属于堆了（实际上的堆是数组未排序的部分），之后堆尾元素为5，堆的大小为4
4.然后再调整数组中尚未排序的部分（也就是新堆），即将堆顶元素递归地下沉，使新堆保持堆的性质。
5.如此循环往复，完成排序。

代码

1.堆排序实现函数

void heapsort(vector<int> &array){
    /*从数组未排序的部分（堆)的最后一个根节点开始，逐步向上遍历每一个根节点并调整堆，
    使其符合大顶堆的性质*/
    for(int i=array.size()/2-1;i>=0;--i){
        adjust(array,i,array.size());
    }
    for(int i=array.size()-1;i>=0;i--){
        /*经过一轮调整后，数组首元素已经为最大元素
        将最大元素移动到当前堆的最后一个元素的位置，之后该元素不再属于堆
        然后再维护堆，看是否需要将新的的首元素下沉，使其符合堆的性质*/
        swap(array[0],array[i]);
        adjust(array,0,i);   //交换后堆的大小缩小为i
    }
}

2.堆的向下调整函数

void adjust(vector<int> &array,int parent,int size){

    /*若parent不是最大节点，通过递归的调用使其不断下沉，以符合堆的性质*/
    /***注意：这里的数组下标从0开始，故求n双亲的下标为（n-1）/2；
    但数组下标若从1开始，求n双亲的下标为n/2；
    同理，如果数组下标从0开始，两个儿子下标为n*2+1和n*2+2；
    但数组下标若从1开始，则两个儿子下标为n*2和n*2+1；***/
    int  max=parent;
    int left=2*parent+1;
    int right=2*parent+2;
    if(left<size&&array[max]<array[left]){
        max=left;
    }
    if(right<size&&array[max]<array[right]){
        max=right;
    }
    if(max==parent) return;
    else{
        //如果当前根节点非最大节点，那么将其与最大节点交换
        //也就是让子节点上来，根节点parent下沉到子节点的位置，然后继续向下递归地调整
        swap(array[max],array[parent]);
        adjust(array,max,size);
    }
}

3、主函数检测

int main(){
    vector<int> array;

    cout<<"依次输入数组的值："<<endl;
    int temp;
    while(cin>>temp){
        array.push_back(temp);
    }

    
    cout<<"排序前数组为:"<<endl;
    for(auto i:array){
        cout<<i;
    }
    cout<<endl;

    heapsort(array);

    cout<<"排序后数组为"<<endl;
    for(auto i:array){
        cout<<i;
    }
    cout<<endl;

    system("pause");
    return 0;
}

输出