数据结构与算法（十二）——算法-动态规划

一、青蛙跳台阶&斐波那契数列

1、问题

　　一只青蛙跳台阶，每次可以跳 1 层或 2 层。青蛙跳到 n 层一共有多少种跳法？

2、思想

　　先把问题规模缩小，考虑 n = 1时，n = 2的解。那么，显然有：

　　（1）边界条件：dp[1] = 1、dp[2] = 2
　　（2）再考虑 n = 3时，逆向思维一下，要跳 3 层，是不是只能是从第 2 阶跳 1 层到或者是从第 1 阶跳 2 层到。所以dp[3] = dp[2] + dp[1]。
　　（3）同理n = 4时，是不是也是只能是从第 3 阶跳 1 层到或者是从第 2 阶跳 2 层到。所以dp[4] = dp[3] + dp[2]。
　　（3）……
　　（4）同理可得，状态转移方程：dp[n] = dp[n - 1] + dp[n - 2]。

3、代码示例

// 递归.时间复杂度:O(2^n).空间复杂度:O(1)
public int jumpFloor(int target) {
    if (target == 1) {
        return 1;
    }
    if (target == 2) {
        return 2;
    }

    return jumpFloor(target - 1) + jumpFloor(target - 2);
}

// 循环（dp数组）.时间复杂度:O(n).空间复杂度:O(n)
public int jumpFloor2(int target) {
    if (target == 1) {
        return 1;
    }

    int[] dp = new int[target + 1];
    dp[1] = 1;
    dp[2] = 2;
    for (int i = 3; i <= target; i++) {
        dp[i] = dp[i - 1] + dp[i - 2];
    }
    return dp[target];
}

// 滚动数组.时间复杂度:O(n).空间复杂度:O(1)
public int jumpFloor3(int target) {
    if (target == 1) {
        return 1;
    }
    int num1 = 1, num2 = 2, temp = num2;

    for (int i = 3; i <= target; i++) {
        temp = num1 + num2;
        num1 = num2;
        num2 = temp;
    }

    return temp;
}

二、网格路径

1、问题

　　有一个 m*n 的网格，从 [1, 1] 出发，每次只能向右或向下，抵达 [m, n] 一共有多少种方案？如图：

2、思想

　　先把问题规模缩小，考虑从 [1, 1]到 [1, 2]，到 [1, 3]，到 [1, 4]……和从 [1, 1]到[2, 1]，到 [3, 1]……，是不是只能一直向右和向下，那么，显然有：
　　（1）边界条件：dp[1][n]  = 1、dp[m][1] = 1
　　（2）再考虑到 [2, 2] ，是不是只有 [1, 2] 向下或者 [2, 1] 向右。所以dp[2][2] = dp[1][2] + dp[2][1]。
　　（3）同理可得，状态转移方程：dp[m][n] = dp[m - 1][n] + dp[m][n - 1]。

3、代码示例

// 3*6. m=3,n=6
public static int gridPath(int m, int n) {
    int[][] dp = new int[m + 1][n + 1];
    for (int i = 1; i <= n; i++) {
        dp[1][i] = 1;
    }

    for (int i = 1; i <= m; i++) {
        dp[i][1] = 1;
    }

    // 遍历二维数组
    for (int i = 2; i <= m; i++) {
        for (int j = 2; j <= n; j++) {
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
        }
    }

    return dp[m][n];
}

三、最长递增子序列

1、问题

　　问题很好理解。例如：[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列，但它不是递增的。

　　nums = [10,9,2,5,3,7,101,18] --> 4 [2,3,7,101] 或者 [2,3,7,18]
　　nums = [0,1,0,3,2,3] --> 4 [0,1,2,3]
　　nums = [7,7,7,7,7,7,7] --> 1 [7]

2、思想

　　定义：dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。为了理解这个定义，比如：dp[3] 就是以 nums[3] = 4 结尾的最长递增子序列（1,3,4）的长度，也就是3。

　　根据这个定义，最终结果（子序列的最大长度）应该是 dp 数组中的最大值。

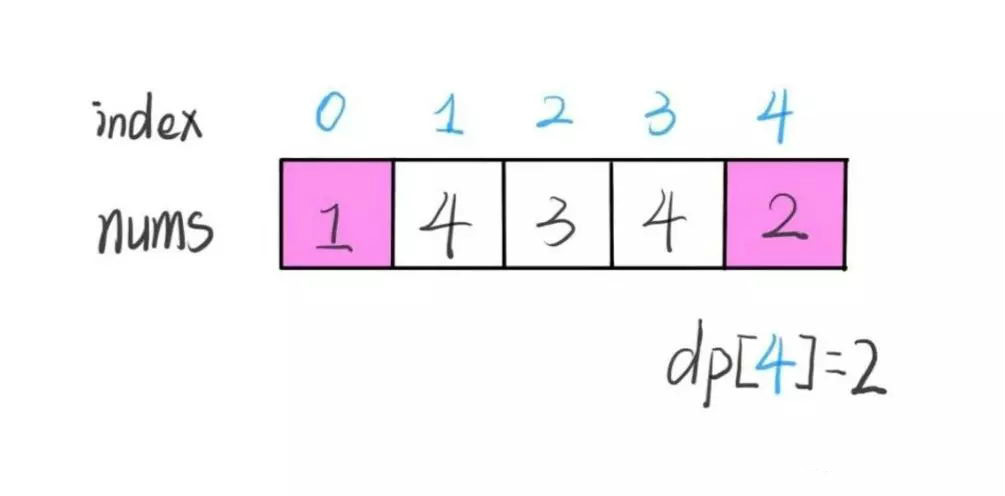
　　过程动图

　　那么，显然有：
　　（1）边界条件：dp[*] = 1
　　（2）动态转移方程：dp[i] = nums[i] > nums[j] && max(dp[i], dp[j] + 1)

3、代码示例

// 时间复杂度 O(N^2)
public int lis(int[] nums) {
    int[] dp = new int[nums.length];
    // dp数组全部初始化为 1
    Arrays.fill(dp, 1);

    for (int i = 0; i < nums.length; i++) {
        for (int j = 0; j < i; j++) {
            if (nums[i] > nums[j]) {
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
    }

    int res = 0;
    for (int i : dp) {
        res = Math.max(res, i);
    }

    return res;
}

四、最长回文子串

1、问题

　　给定一个字符串 s，长度为 n，找到 s 中最长的回文子串。

　　s = "abbac" --> "abba"
　　s = "cbbd" --> "bb"
　　s = "babad" --> "aba"

2、思想

　　定义：dp[i][j]表示 s 中 i 到 j 的字符串是否是回文串。那么，显然有：
　　（1）边界条件：dp[i][i] = true；dp[i][j] = true 当 s[i] = s[j] && j - i = 1
　　（2）状态转移方程：dp[i][j] = ( s[i] = s[j] && dp[i + 1][j - 1] )

3、代码示例

public int getLongestPalindrome(String s, int n) {
    boolean[][] dp = new boolean[n][n];
    int max = 1;

    // 字符串首尾字母长度差 (len = j - i) 0~n-1
    for (int len = 0; len < n; len++) {

        for (int i = 0; i < n - len; i++) {
            int j = i + len;

            // 如果字符串 i 到 j 的首尾相等，再根据字符串 i+1 到 j-1 来确定，即得到递推公式
            if (s.charAt(i) == s.charAt(j)) {
                // 边界条件
                if (len == 0 || len == 1) {
                    dp[i][j] = true;
                } else {
                    // 状态转移方程
                    dp[i][j] = dp[i + 1][j - 1];
                }

                if (dp[i][j]) {
                    // 更新最大长度
                    max = Math.max(max, len + 1);
                }
            }
        }
    }
    return max;
}

五、兑换硬币

1、问题

　　给定一个正整数数组 coins，表示不同面值的硬币，整数 amount 代表总金额。求可以凑成总金额所需的最少硬币个数，不能组成总金额，返回 -1。硬币数量无限。

　　coins = [1,3,5], amout = 11 -> 3（11 = 5 + 5 + 1）
　　coins = [2,5], amout = 3 -> -1

2、思想

　　用dp[i] = j 表示凑够 i 元最少需要 j 个硬币。先把问题规模缩小，考虑，如果有面值为1元、3元和5元的硬币若干枚，如何用最少的硬币凑够11元？答案很简单是 3（5+5+1）。则：
　　i = 0，表示凑够0元最少需要的硬币数。当然就是不选硬币，需要0个硬币。

　　dp[0] = 0

　　i = 1，只有1元可用，选择 1 元硬币，金额变为 i - 1 = 0，接下来只需要凑够 0 元即可。

　　dp[1] = dp[i - 1] + 1 = dp[0] + 1 = 0 + 1 = 1

　　i = 2，只有1元可用，选择 1 元硬币，金额变为 i - 1 = 1，接下来只需要凑够 1 元即可。

　　dp[2] = dp[i - 1] + 1 = dp[1] + 1 = 1 + 1 = 2

　　i = 3，可选硬币有 1 和 3，则分两种情况
　　①选择 1 元硬币，金额变为 i - 1 = 2，接下来只需要凑够 2 元即可。

　　dp[3] = dp[i - 1] + 1 = dp[2] + 1 = 3 （3个1元的）

　　②选择 3 元硬币，金额变为 i - 3 = 0，接下来只需要凑够 0 元即可。

　　dp[3] = dp[i - 3] + 1 = dp[0] + 1 = 1 （1个3元的）

　　显然，上述情况取小：

　　dp[3] = min{dp[i - 1] + 1, dp[i - 3] + 1} = 1

　　i = 4~amount，同理可得。

　　归纳一下：在已知dp[0]、dp[1]、dp[2]、……dp[i - 1]求 dp[i] 时，在可取的硬币面值（i >= coins[j]，coins[j]表示第 j 个硬币的面值），都取一次，则问题就可降级为 dp[i - coins[j]]，而这个值是已知，最后取小即可。
　　案例说明：

　　不妨：coins = [1,3,5,20]，求dp[11].
　　目的是凑成11，那么，从可选的硬币里选择一枚，所有情况如下：
　　选择coins[0]=1，则还需要凑11-1=10，即，在arr中凑10，所以dp[11]=dp[10] + 1。
　　选择coins[1]=3，则还需要凑11-3=8，即，在arr中凑8，所以dp[11]=dp[11-3] + 1。
　　选择coins[2]=5，则还需要凑11-5=6，即，在arr中凑6，所以dp[11]=dp[11-5] + 1。
　　注意：coins[3]=20 > 11，是不可选的。所以可选条件是 i >= coins[j]。
　　最后，在上述情况取小即可。

　　那么，有：
　　（1）边界条件：dp[0] = 0
　　（2）状态转移方程：dp[i] = min(dp[i], dp[i - coins[j]] + 1)。i - coins[j] >= 0

3、代码示例

// 兑换硬币
public int minMoney(int[] coins, int amount) {
    // 数组下标从 0 开始
    int[] dp = new int[amount + 1];

    // 若最小硬币是 1,那么兑换 amount 最多用 amount 个硬币。则 dp[amount] 最大等于 amount
    // 由于下面要取小，所以给一个越界值
    Arrays.fill(dp, amount + 1);

    // 边界条件
    dp[0] = 0;
    // 依次求dp[1]、dp[2]……dp[amount]
    for (int i = 1; i < amount + 1; i++) {

        // 遍历硬币的面值
        for (int coin : coins) {
            // 该硬币面值可取
            if (i - coin >= 0) {
                dp[i] = Math.min(dp[i], dp[i - coin] + 1);
            }
        }
    }

    // 要是流程走下来 dp 值是非法值.说明换不出来
    return dp[amount] == amount + 1 ? -1 : dp[amount];
}

　　注：贪心不正确
　　coins = [1,4,5,7], amout=17
　　贪心结果：7+7+1+1+1 -> 5
　　实际：7+5+4+1 ->4

六、0-1背包问题

1、问题

　　一共有N件物品，第i（i从1开始）件物品的重量为w[i]，价值为v[i]。在总重量不超过背包容量C的情况下，能够装入背包的最大价值是多少？
　　通俗的说，就是你有一个麻袋，你去超市顺便拿东西，在不超出麻袋容量的情况下，尽可能的拿的物品价值和最大。
　　要求：①装入背包的总价值最大，且重量不超出。②物品要么拿，要么不拿，不可重复拿。

2、思想

　　举一个案例，有一个背包，容量为4kg，现有物品：

物品	重量	价值
吉他（G）	1kg	1500
音响（S）	4kg	3000
电脑（L）	3kg	2000

　　显然：可取方案有G+L，价值3500；或S，价值3000。最佳方案：G+L，3500。
　　定义：dp[i][j]表示在前 i 个物品中选择，能够装入容量为 j 的背包中的最大价值。即：

物品\重量	0kg	1kg	2kg	3kg	4kg
	0	0	0	0	0
吉他（G）	0
音响（S）	0
电脑（L）	0

　　先把问题规模缩小，按一行一行（必须），背包容量为0、1、2、……C=4的顺序，填写上表。
　　表示物品只有吉他，有：

物品\重量	0kg	1kg	2kg	3kg	4kg
	0	0	0	0	0
吉他（G）	0	1500	1500	1500	1500
音响（S）	0
电脑（L）	0

　　表示物品有吉他、音响，有：

物品\重量	0kg	1kg	2kg	3kg	4kg
	0	0	0	0	0
吉他（G）	0	1500	1500	1500	1500
音响（S）	0	1500	1500	1500	3000
电脑（L）	0

　　表示物品有吉他、音响、电脑，有：

物品\重量	0kg	1kg	2kg	3kg	4kg
	0	0	0	0	0
吉他（G）	0	1500	1500	1500	1500
音响（S）	0	1500	1500	1500	3000
电脑（L）	0	1500	1500	2000	3500

　　那么，有：
　　（1）边界条件：dp[i][0] = dp[0][j] = 0。上表格第一列、第一行为0
　　（2）状态转移方程：dp[i][j] = max(dp[i - 1][j], v[i] + dp[i - 1][j - w[i]])

3、代码示例

public class Knapsack {
    private Goods[] goods;
    // 背包的容量
    private int c;
    // dp[i][j]:表示在前i个物品中选择,能够装入容量为j的背包中的最大价值
    private int[][] dp;
    private int[][] path;

    public Knapsack(Goods[] goods, int c) {
        if (goods == null || goods.length == 0 || c <= 0) {
            return;
        }
        this.goods = goods;
        this.c = c;

        this.dp = new int[goods.length][c + 1];
        this.path = new int[goods.length][c + 1];

        // 初始化第一列、第一行为0.可不写,默认就是0
//        for (int i = 0; i < dp.length; i++) {
//            dp[i][0] = 0;
//        }
//        for (int i = 0; i < dp[0].length; i++) {
//            dp[0][i] = 0;
//        }
    }

    // 动态规划
    public void dp() {
        for (int i = 1; i < dp.length; i++) {
            for (int j = 1; j < dp[0].length; j++) {
                // 表明当前物品放不了背包
                if (goods[i].weight > j) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], goods[i].value + dp[i - 1][j - goods[i].weight]);

                    // 用于记录物品选择策略
                    if (dp[i - 1][j] < goods[i].value + dp[i - 1][j - goods[i].weight]) {
                        path[i][j] = 1;
                    }
                }
            }
        }

    }

    // 获取物品的选择策略
    public List<Goods> getPlan() {
        // 1.查看 dp 填写情况
        for (int i = 0; i < dp.length; i++) {
            for (int j = 0; j < dp[i].length; j++) {
                System.out.print(dp[i][j] + " ");
            }
            System.out.println();
        }

        // 2.物品选择策略
        List<Goods> result = new ArrayList<>();
        int i = path.length - 1;
        int j = path[0].length - 1;
        // 从path的最后一个开始找
        while (i > 0 && j > 0) {
            if (path[i][j] == 1) {
                result.add(goods[i]);

                j = j - goods[i].weight;
            }
            i--;
        }
        return result;
    }
}

// 物品
class Goods {
    public String name;
    // 物品重量
    public int weight;
    // 物品价值
    public int value;

    public Goods(String name, int weight, int value) {
        this.name = name;
        this.weight = weight;
        this.value = value;
    }

    @Override
    public String toString() {
        return "Goods{" +
                "name='" + name + '\'' +
                ", weight=" + weight +
                ", value=" + value +
                '}';
    }
}

public class Main {
    public static void main(String[] args) {
        Goods[] goods = new Goods[4];

        // 为了使得 goods[1] 是第1个物品
        goods[0] = null;
        goods[1] = new Goods("吉他", 1, 1500);
        goods[2] = new Goods("音响", 4, 3000);
        goods[3] = new Goods("电脑", 3, 2000);

        // 背包容量
        final int C = 4;
        Knapsack knapsack = new Knapsack(goods, C);
        System.out.println("动态规划dp:");
        knapsack.dp();

        final List<Goods> plan = knapsack.getPlan();
        System.out.println("物品选择策略:");
        System.out.println(plan);
    }
}

// 结果
动态规划dp:
0 0 0 0 0 
0 1500 1500 1500 1500 
0 1500 1500 1500 3000 
0 1500 1500 2000 3500 
物品选择策略:
[Goods{name='电脑', weight=3, value=2000}, Goods{name='吉他', weight=1, value=1500}]

4、说明

　　0-1背包问题不太好理解。下面用一些图文帮助读者理解。
　　首先，我们深刻理解一下0-1背包的问题，如图：

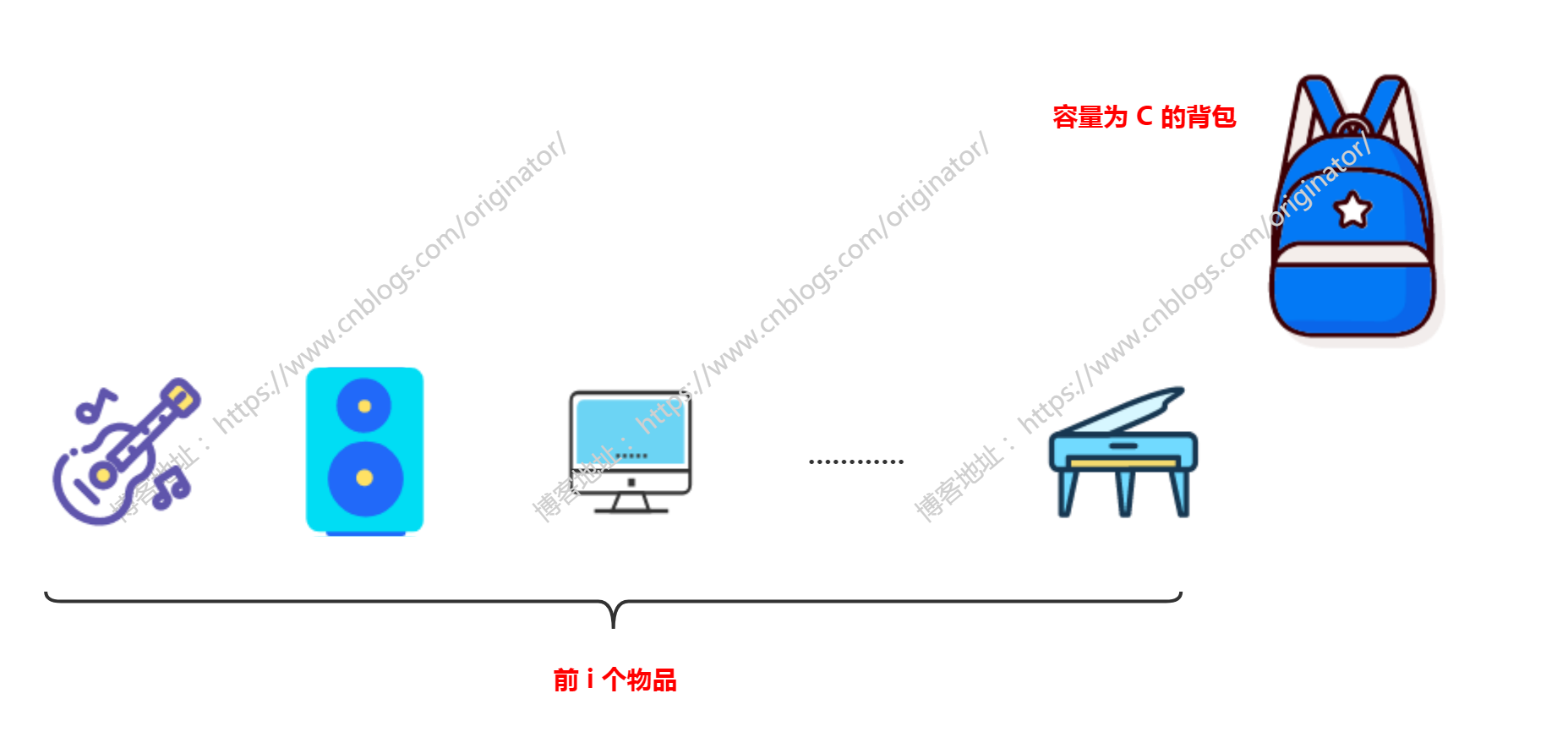
　　不妨假设，在这前 i 个物品中，选取总重量不超过背包容量 C 的物品，且使得物品总价值最大。选择策略叫方案A，此时的最大总价值设为 maxValue。这里理解一下前 i 个物品，由于动态规划问题是规模逐渐增大的，所以，要姑且把物品看成是"有序的"。

　　那么，我们思考一个问题，如果此时来了第 i + 1个物品（价值：V，重量：W），会怎么样呢？如图：

　　主要分为两种情况谈论：
　　1、W > C ：第 i + 1 个物品（钻石）不可取。那么，此时（总体物品是 i + 1个，但是）是不是就相当于没有第 i + 1 这个物品（因为在i + 1个物品中选择，不会取到第 i + 1这个物品），问题的解，是不是就等价于图一（在 i 个物品中选择，背包容量为C），所以，就是方案A，最大总价值就是 maxValue。
　　2、W <= C ：第 i + 1个物品（钻石）可取。又分为两种情况：即拿或不拿。（注：这是0-1背包，一个物品要么不选择，要么只选择一次）
　　　　2.1：不拿。同样，此时（这种情况下）问题的解，与上述（W > C）相同，即方案A，最大总价值就是 maxValue
　　　　2.2：拿。那么，第 i + 1 个物品（钻石）已经被选择了，此时背包容量还有（C - W）。由于第 i + 1个物品已经被选择了，此时问题规模，就是在前 i 个物品中，选取总重量不超过背包容量 C - W 的物品。价值就是dp[i][c - w]。
　　由于2.1和2.2属于一种情况。所以整个问题的解就是 max( maxValue， V + dp[i][c - w] )。

　　下面，再对上面填表的过程，以及代码做一些解释：