数据结构与算法(七)——图
一、图
1、介绍
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为:G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
无向完全图:在无向图中,任意两个顶点之间都存在边。含有 n 个顶点的无向完全图有 n*(n - 1)/2 条边。
有向完全图:在有向图中,任意两个顶点之间都存在弧。含有 n 个顶点的有向完全图有 n*(n - 1)条边。
通常认为边或弧数小于 n*logn (n是顶点个数)的图为稀疏图,反之为稠密图。
2、图的存储结构
邻接矩阵:适用稠密图
无向图
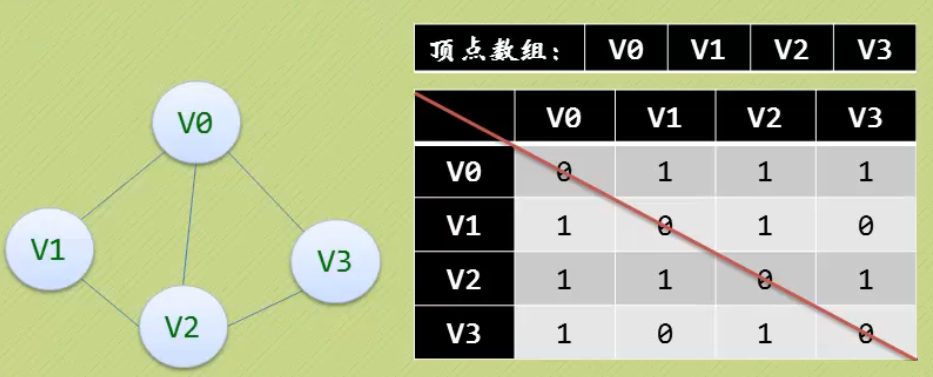
有向图
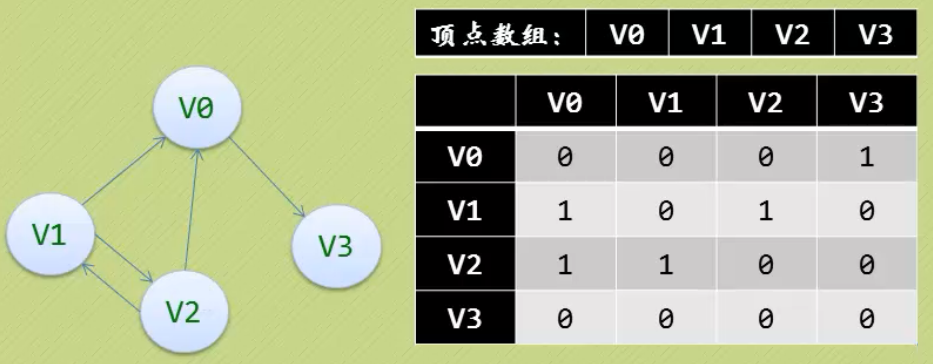
网
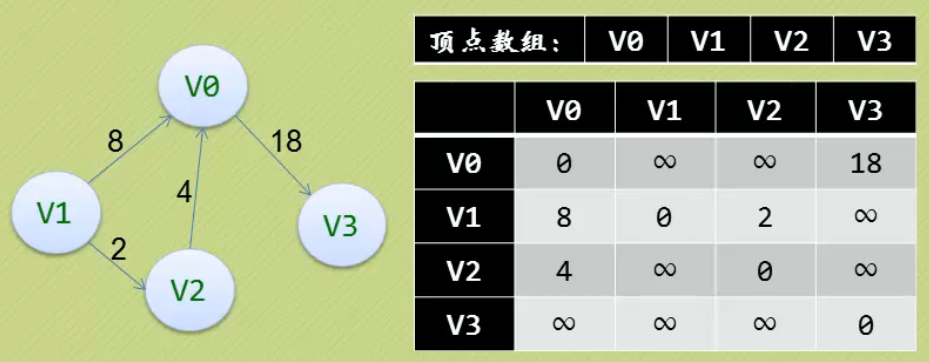
邻接表:适用稀疏图
无向图
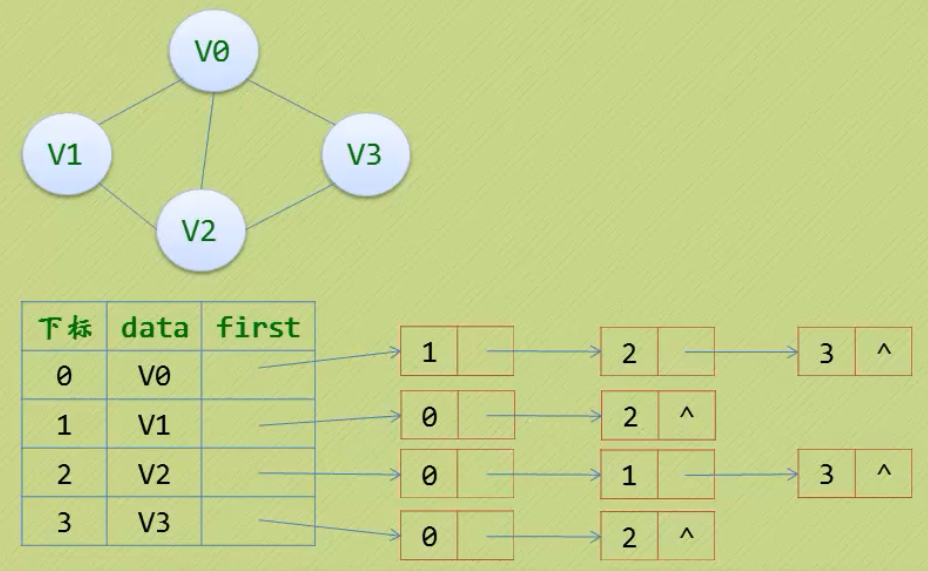
有向图-顶点当弧尾
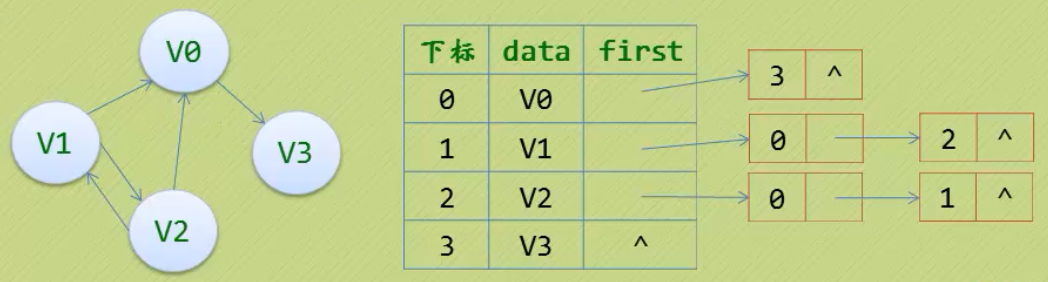
有向图-顶点当弧头
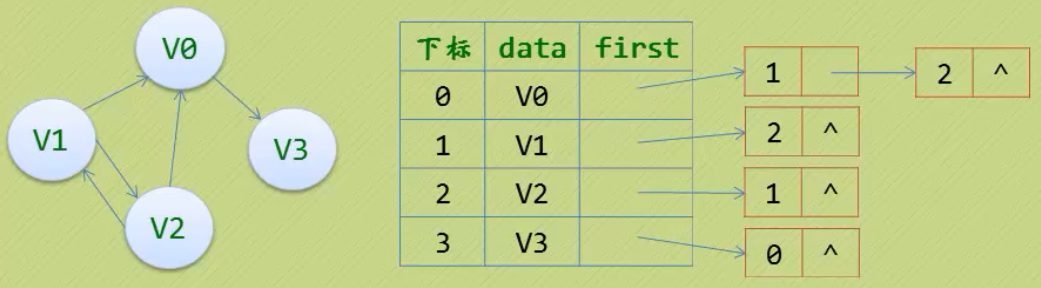
有向图-网
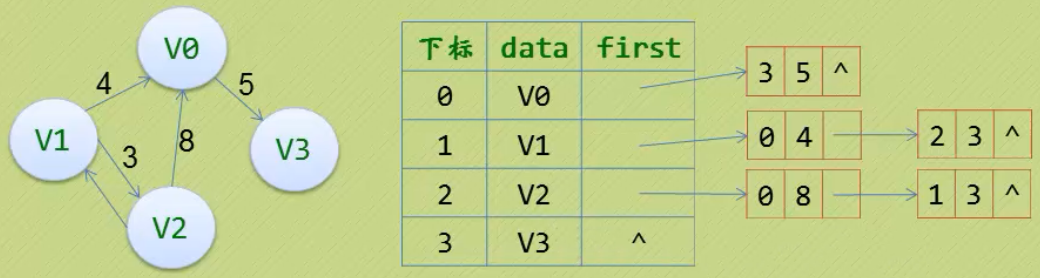
3、图的遍历
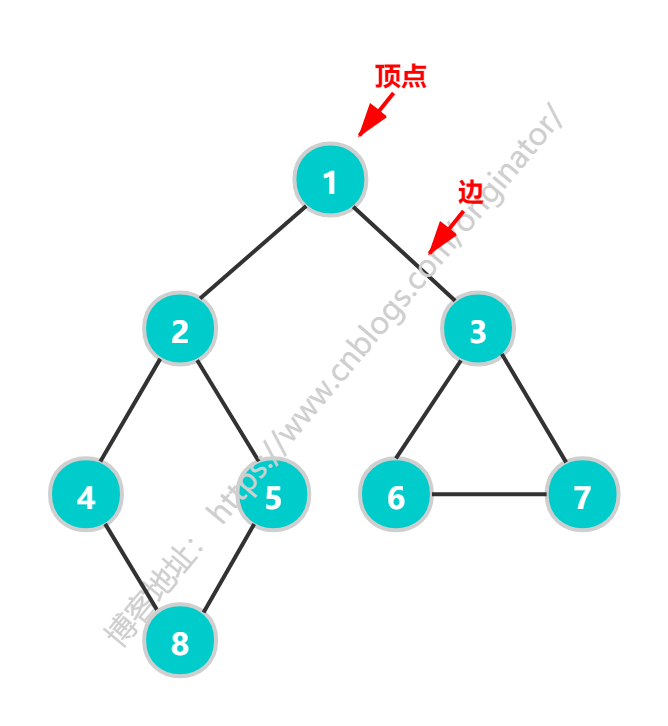
深度优先遍历顺序为:1->2->4->8->5->3->6->7
广度优先遍历顺序为:1->2->3->4->5->6->7->8
深度优先遍历(DepthFirstSearch:DFS):类似于树的前序遍历
思想:略。
代码示例:见后
广度优先遍历(BreadthFirstSearch:BFS):类似于树的层序遍历
思想:需要一个辅助队列。
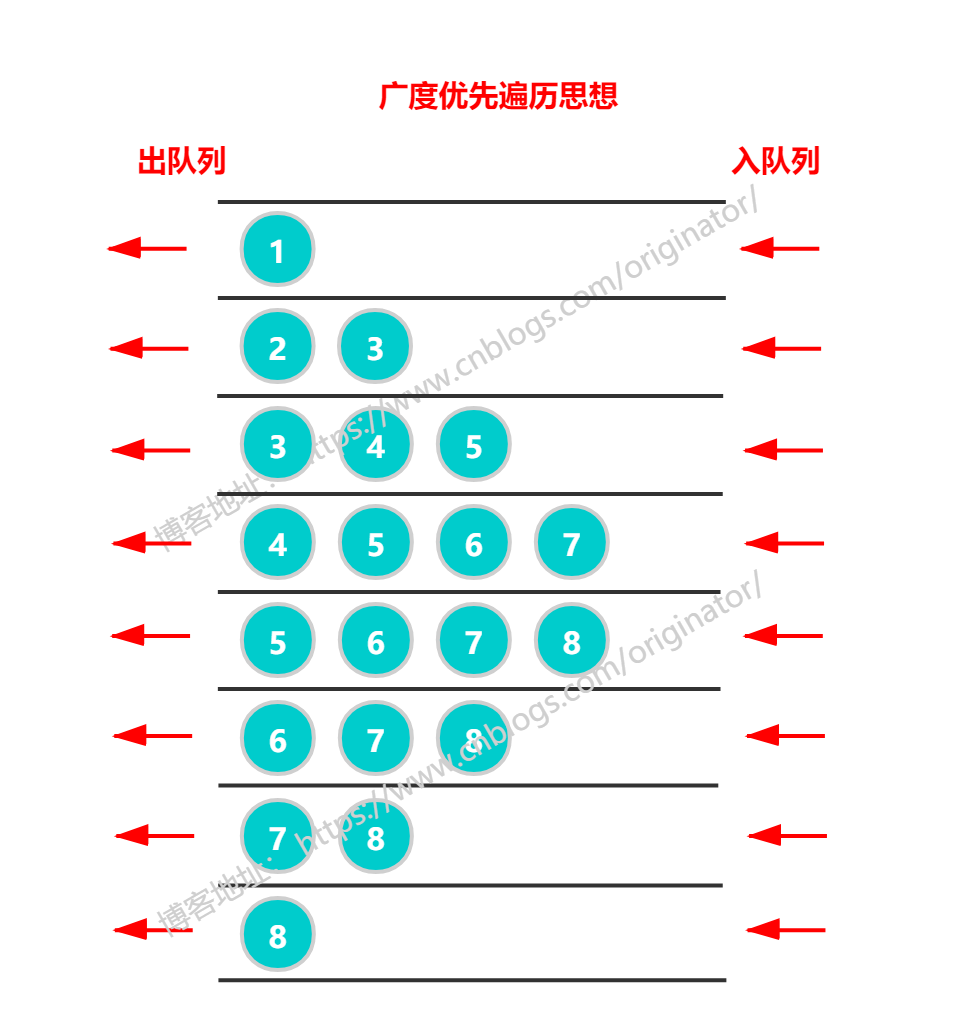
代码示例:深度优先、广度优先

1 public class Graph { 2 3 // 顶点集 4 private List<String> vertex; 5 // 邻接矩阵 6 private int[][] matrix; 7 8 public Graph(String[] vertex, int[][] matrix) { 9 if (vertex == null || vertex.length == 0 || matrix == null) { 10 return; 11 } 12 13 // 初始化顶点集 14 this.vertex = new ArrayList<>(Arrays.asList(vertex)); 15 16 // 初始化邻接矩阵 17 this.matrix = new int[vertex.length][vertex.length]; 18 for (int i = 0; i < vertex.length; i++) { 19 System.arraycopy(matrix[i], 0, this.matrix[i], 0, vertex.length); 20 } 21 } 22 23 // 深度优先遍历 24 public void dfs() { 25 // 记录某个结点是否被访问 26 boolean[] visited = new boolean[vertex.size()]; 27 for (int i = 0; i < vertex.size(); i++) { 28 if (!visited[i]) { 29 this.dfs(visited, i); 30 } 31 } 32 } 33 34 private void dfs(boolean[] visited, int i) { 35 System.out.print(vertex.get(i) + "->"); 36 visited[i] = true; 37 38 int w = this.getFirstNeighbor(i); 39 // 找到 40 while (w != -1) { 41 if (!visited[w]) { 42 dfs(visited, w); 43 } 44 // w已经被访问过 45 w = getNextNeighbor(i, w + 1); 46 } 47 48 } 49 50 // 广度优先遍历 51 public void bfs() { 52 // 记录某个结点是否被访问 53 boolean[] visited = new boolean[vertex.size()]; 54 for (int i = 0; i < vertex.size(); i++) { 55 if (!visited[i]) { 56 this.bfs(visited, i); 57 } 58 } 59 } 60 61 private void bfs(boolean[] visited, int i) { 62 System.out.print(vertex.get(i) + "->"); 63 visited[i] = true; 64 65 // 队列.记录结点访问顺序 66 Queue<Integer> queue = new LinkedList<>(); 67 queue.offer(i); 68 69 while (!queue.isEmpty()) { 70 final Integer u = queue.poll(); 71 72 // 得到u的第一个邻接结点的下标w 73 int w = this.getFirstNeighbor(u); 74 while (w != -1) { 75 if (!visited[w]) { 76 System.out.print(vertex.get(w) + "->"); 77 visited[w] = true; 78 queue.offer(w); 79 } 80 // 以u为前驱,找w后的下一个邻接点 81 w = this.getNextNeighbor(u, w + 1); 82 } 83 } 84 } 85 86 private int getFirstNeighbor(int index) { 87 return this.getNextNeighbor(index, 0); 88 } 89 90 // 根据前一个邻接结点的下标来获取下一个邻接结点 91 private int getNextNeighbor(int index, int v2) { 92 for (int j = v2; j < vertex.size(); j++) { 93 if (matrix[index][j] > 0) { 94 return j; 95 } 96 } 97 98 return -1; 99 } 100 101 // 显示图的邻接矩阵 102 public void showGraph() { 103 for (int[] link : this.matrix) { 104 System.out.println(Arrays.toString(link)); 105 } 106 } 107 108 }
代码示例:测试类

1 public class Main { 2 public static void main(String[] args) { 3 String[] vertex = {"1", "2", "3", "4", "5", "6", "7", "8"}; 4 5 int[][] matrix = { 6 /*1*//*2*//*3*//*4*//*5*//*6*//*7*//*8*/ 7 /*1*/ {0, 1, 1, 0, 0, 0, 0, 0}, 8 /*2*/ {0, 0, 0, 1, 1, 0, 0, 0}, 9 /*3*/ {0, 0, 0, 0, 0, 1, 1, 0}, 10 /*4*/ {0, 0, 0, 0, 0, 0, 0, 1}, 11 /*5*/ {0, 0, 0, 0, 0, 0, 0, 1}, 12 /*6*/ {0, 0, 0, 0, 0, 0, 1, 0}, 13 /*7*/ {0, 0, 0, 0, 0, 0, 0, 0}, 14 /*8*/ {0, 0, 0, 0, 0, 0, 0, 0}}; 15 16 Graph graph = new Graph(vertex, matrix); 17 18 graph.showGraph(); 19 System.out.print("深度优先:"); 20 graph.dfs(); 21 22 System.out.print("\n广度优先:"); 23 graph.bfs(); 24 } 25 }
二、最小生成树
生成树上边的权值之和达到最小。不成环。
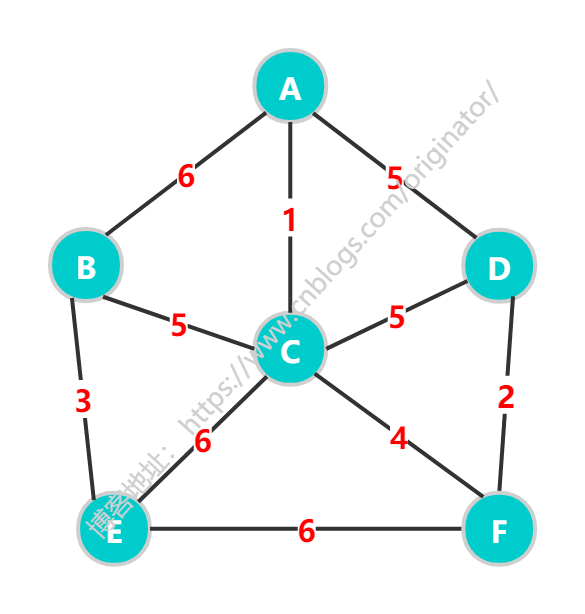
1、普里姆算法(Prim)
针对顶点来展开,适用于稠密图。
思想:
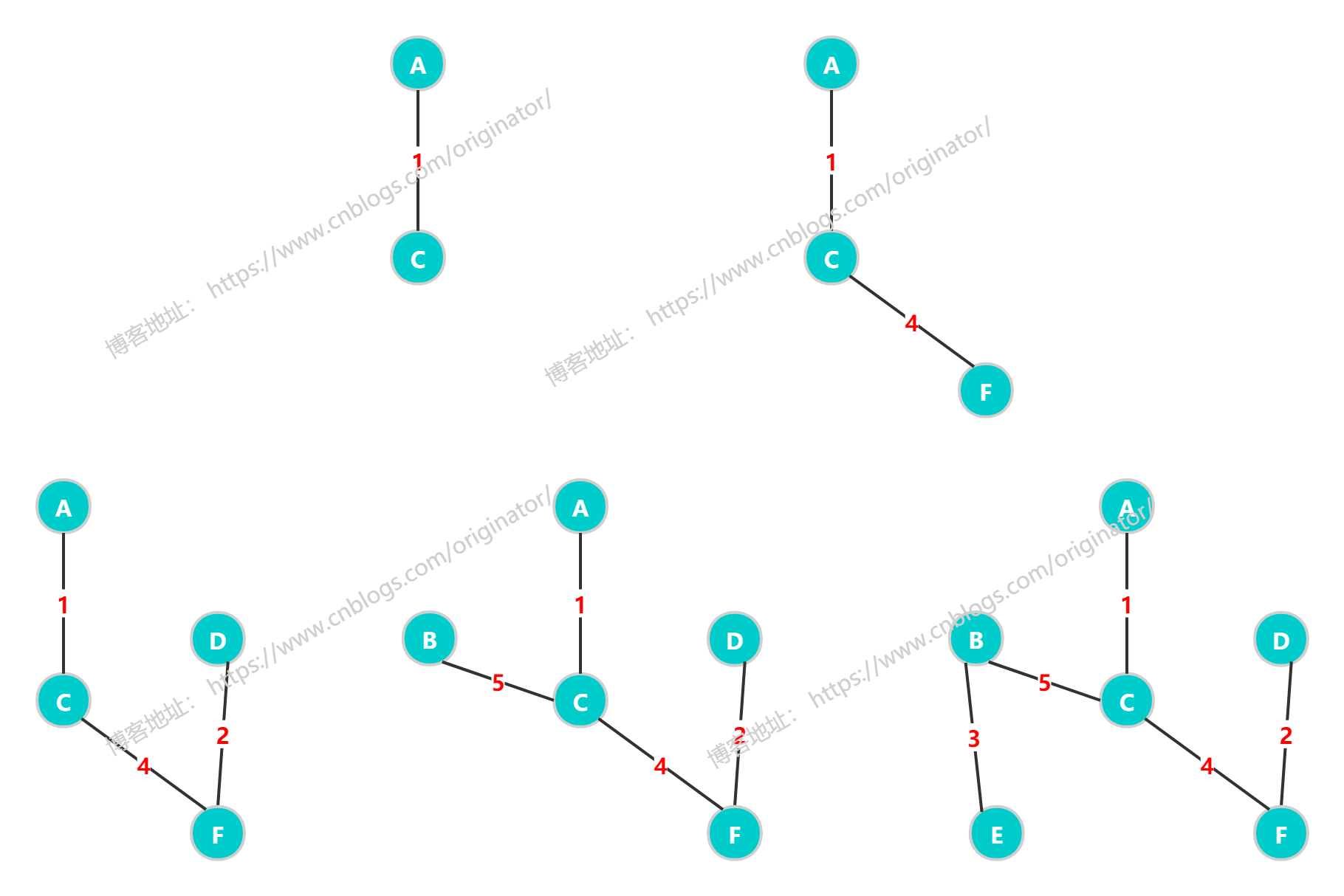
代码示例:Prim

1 public class Graph { 2 3 // 顶点集 4 private List<String> vertex; 5 // 邻接矩阵 6 private int[][] matrix; 7 8 public Graph(String[] vertex, int[][] matrix) { 9 if (vertex == null || vertex.length == 0 || matrix == null) { 10 return; 11 } 12 13 // 初始化顶点集 14 this.vertex = new ArrayList<>(Arrays.asList(vertex)); 15 16 // 初始化邻接矩阵 17 this.matrix = new int[vertex.length][vertex.length]; 18 for (int i = 0; i < vertex.length; i++) { 19 System.arraycopy(matrix[i], 0, this.matrix[i], 0, vertex.length); 20 } 21 } 22 23 /** 24 * prim 算法生成最小生成树 25 * 26 * @param v 表示从图的第v个顶点开始生成 'A'->0 'B'->1 27 */ 28 public List<Edge> prim(int v) { 29 if (v < 0 || v >= this.vertex.size()) { 30 return new ArrayList<>(); 31 } 32 33 final int size = this.vertex.size(); 34 boolean[] visited = new boolean[size]; 35 List<Edge> result = new ArrayList<>(); 36 37 // 当前结点标记为已访问 38 visited[v] = true; 39 int h1 = -1; 40 int h2 = -1; 41 int minWeight = Integer.MAX_VALUE; 42 for (int k = 1; k < size; k++) { 43 //这个是确定每一次生成的子图,和哪个结点的距离最近 44 for (int i = 0; i < size; i++) {// i结点表示被访问过的结点 45 for (int j = 0; j < size; j++) {//j结点表示还没有访问过的结点 46 if (visited[i] && !visited[j] && this.matrix[i][j] > 0 && this.matrix[i][j] < minWeight) { 47 //替换minWeight(寻找已经访问过的结点和未访问过的结点间的权值最小的边) 48 minWeight = this.matrix[i][j]; 49 h1 = i; 50 h2 = j; 51 } 52 } 53 } 54 //找到一条边是最小 55 //System.out.println("边<" + this.vertex.get(h1) + "," + this.vertex.get(h2) + "> 权值:" + minWeight); 56 result.add(new Edge(vertex.get(h1), vertex.get(h2), minWeight)); 57 58 //将当前这个结点标记为已经访问 59 visited[h2] = true; 60 //minWeight 重新设置为最大值 10000 61 minWeight = Integer.MAX_VALUE; 62 } 63 64 return result; 65 } 66 67 // 显示图的邻接矩阵 68 public void showGraph() { 69 for (int[] link : this.matrix) { 70 System.out.println(Arrays.toString(link)); 71 } 72 } 73 74 public static class Edge implements Comparable<Edge> { 75 private final String start; 76 private final String end; 77 private final int weight; 78 79 public Edge(String start, String end, int weight) { 80 this.start = start; 81 this.end = end; 82 this.weight = weight; 83 } 84 85 @Override 86 public String toString() { 87 return "Edge{" + 88 "start='" + start + '\'' + 89 ", end='" + end + '\'' + 90 ", weight=" + weight + 91 '}'; 92 } 93 94 @Override 95 public int compareTo(Edge o) { 96 return this.weight - o.weight; 97 } 98 } 99 100 }
代码示例:测试类

1 public class Main { 2 public static void main(String[] args) { 3 String[] vertex = {"A", "B", "C", "D", "E", "F"}; 4 5 int[][] matrix = { 6 /*A*//*B*//*C*//*D*//*E*//*F*/ 7 /*A*/ {0, 6, 1, 5, -1, -1}, 8 /*B*/ {6, 0, 5, -1, 3, -1}, 9 /*C*/ {1, 5, 0, 5, 6, 4}, 10 /*D*/ {5, -1, 5, 0, -1, 2}, 11 /*E*/ {-1, 3, 6, -1, 0, 6}, 12 /*F*/ {-1, -1, 4, 2, 6, 0}}; 13 14 Graph graph = new Graph(vertex, matrix); 15 16 graph.showGraph(); 17 final List<Graph.Edge> prim = graph.prim(1); 18 19 System.out.println("prim算法最小生成树为"); 20 for (Graph.Edge edge : prim) { 21 System.out.println(edge); 22 } 23 } 24 } 25 26 // 结果 27 [0, 6, 1, 5, -1, -1] 28 [6, 0, 5, -1, 3, -1] 29 [1, 5, 0, 5, 6, 4] 30 [5, -1, 5, 0, -1, 2] 31 [-1, 3, 6, -1, 0, 6] 32 [-1, -1, 4, 2, 6, 0] 33 prim算法最小生成树为 34 Edge{start='B', end='E', weight=3} 35 Edge{start='B', end='C', weight=5} 36 Edge{start='C', end='A', weight=1} 37 Edge{start='C', end='F', weight=4} 38 Edge{start='F', end='D', weight=2}
2、克鲁斯卡尔算法(Kruskal)
针对边来展开,适用于稀疏图。
思想:
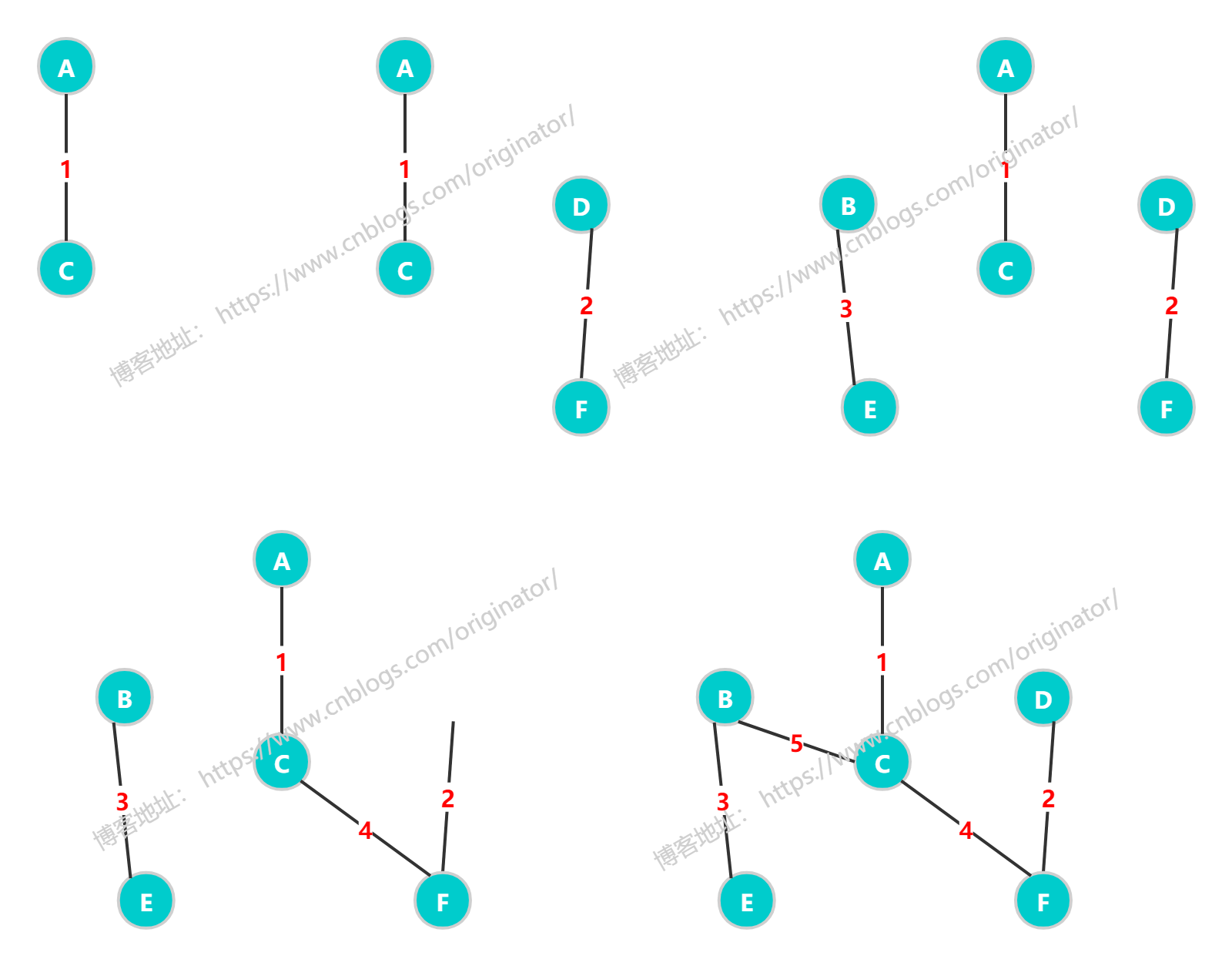
代码示例:Kruskal

1 public class Graph { 2 3 // 顶点集 4 private List<String> vertex; 5 // 邻接矩阵 6 private int[][] matrix; 7 8 public Graph(String[] vertex, int[][] matrix) { 9 if (vertex == null || vertex.length == 0 || matrix == null) { 10 return; 11 } 12 13 // 初始化顶点集 14 this.vertex = new ArrayList<>(Arrays.asList(vertex)); 15 16 // 初始化邻接矩阵 17 this.matrix = new int[vertex.length][vertex.length]; 18 for (int i = 0; i < vertex.length; i++) { 19 System.arraycopy(matrix[i], 0, this.matrix[i], 0, vertex.length); 20 } 21 } 22 23 // Kruskal算法 24 public List<Edge> kruskal() { 25 // 边集 26 List<Edge> edges = this.initEdges(); 27 if (edges.size() == 0) { 28 return new ArrayList<>(); 29 } 30 31 int[] ends = new int[edges.size()]; 32 final Map<String, Integer> vertexMap = this.getVertexMap(); 33 34 List<Edge> result = new ArrayList<>(); 35 36 //遍历edges 数组,将边添加到最小生成树中时,判断是准备加入的边否形成了回路,如果没有,就加入 rets, 否则不能加入 37 Collections.sort(edges); 38 39 for (Edge edge : edges) { 40 final int p1 = vertexMap.get(edge.start); 41 final int p2 = vertexMap.get(edge.end); 42 43 //获取p1这个顶点在已有最小生成树中的终点 44 int m = this.getEnd(ends, p1); 45 //获取p2这个顶点在已有最小生成树中的终点 46 int n = this.getEnd(ends, p2); 47 48 // 没有构成回路 49 if (m != n) { 50 // 设置m在"已有最小生成树"中的终点 51 ends[m] = n; 52 53 result.add(edge); 54 } 55 } 56 57 return result; 58 } 59 60 private Map<String, Integer> getVertexMap() { 61 Map<String, Integer> map = new HashMap<>(); 62 for (int i = 0; i < this.vertex.size(); i++) { 63 map.put(this.vertex.get(i), i); 64 } 65 return map; 66 } 67 68 /** 69 * 获取下标为i的顶点的终点,用于后面判断两个顶点的终点是否相同 70 * 71 * @param ends 数组就是记录了各个顶点对应的终点是哪个,ends 数组是在遍历过程中,逐步形成 72 * @param i 表示传入的顶点对应的下标 73 * @return 下标为i的这个顶点对应的终点的下标 74 */ 75 private int getEnd(int[] ends, int i) { // i = 4 [0,0,0,0,5,0,0,0,0,0,0,0] 76 while (ends[i] != 0) { 77 i = ends[i]; 78 } 79 return i; 80 } 81 82 // 显示图的邻接矩阵 83 public void showGraph() { 84 for (int[] link : this.matrix) { 85 System.out.println(Arrays.toString(link)); 86 } 87 } 88 89 private List<Edge> initEdges() { 90 // 初始化边集 91 List<Edge> edges = new ArrayList<>(); 92 for (int i = 0; i < vertex.size(); i++) { 93 for (int j = i + 1; j < vertex.size(); j++) { 94 if (matrix[i][j] > 0) { 95 edges.add(new Edge(vertex.get(i), vertex.get(j), matrix[i][j])); 96 } 97 } 98 } 99 100 return edges; 101 } 102 103 public static class Edge implements Comparable<Edge> { 104 private final String start; 105 private final String end; 106 private final int weight; 107 108 public Edge(String start, String end, int weight) { 109 this.start = start; 110 this.end = end; 111 this.weight = weight; 112 } 113 114 @Override 115 public String toString() { 116 return "Edge{" + 117 "start='" + start + '\'' + 118 ", end='" + end + '\'' + 119 ", weight=" + weight + 120 '}'; 121 } 122 123 @Override 124 public int compareTo(Edge o) { 125 return this.weight - o.weight; 126 } 127 } 128 129 }
代码示例:测试类

1 public class Main { 2 public static void main(String[] args) { 3 String[] vertex = {"A", "B", "C", "D", "E", "F"}; 4 5 int[][] matrix = { 6 /*A*//*B*//*C*//*D*//*E*//*F*/ 7 /*A*/ {0, 6, 1, 5, -1, -1}, 8 /*B*/ {6, 0, 5, -1, 3, -1}, 9 /*C*/ {1, 5, 0, 5, 6, 4}, 10 /*D*/ {5, -1, 5, 0, -1, 2}, 11 /*E*/ {-1, 3, 6, -1, 0, 6}, 12 /*F*/ {-1, -1, 4, 2, 6, 0}}; 13 14 Graph graph = new Graph(vertex, matrix); 15 graph.showGraph(); 16 17 final List<Graph.Edge> result = graph.kruskal(); 18 19 System.out.println("kruskal算法最小生成树为"); 20 for (Graph.Edge edge : result) { 21 System.out.println(edge); 22 } 23 } 24 } 25 26 // 结果 27 [0, 6, 1, 5, -1, -1] 28 [6, 0, 5, -1, 3, -1] 29 [1, 5, 0, 5, 6, 4] 30 [5, -1, 5, 0, -1, 2] 31 [-1, 3, 6, -1, 0, 6] 32 [-1, -1, 4, 2, 6, 0] 33 kruskal算法最小生成树为 34 Edge{start='A', end='C', weight=1} 35 Edge{start='D', end='F', weight=2} 36 Edge{start='B', end='E', weight=3} 37 Edge{start='C', end='F', weight=4} 38 Edge{start='B', end='C', weight=5}
未完成
作者:Craftsman-L
本博客所有文章仅用于学习、研究和交流目的,版权归作者所有,欢迎非商业性质转载。
如果本篇博客给您带来帮助,请作者喝杯咖啡吧!点击下面打赏,您的支持是我最大的动力!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号