数据结构与算法（六）——二叉树

一、排序二叉树（二叉查找树、二叉搜索树）

1、介绍

　　排序二叉树（Binary Sort Tree），性质：左孩子 < 根结点 < 右孩子。在一般情况下，查询效率比链表要高。
　　按照中序遍历可以得到一个从小到大的有序序列。

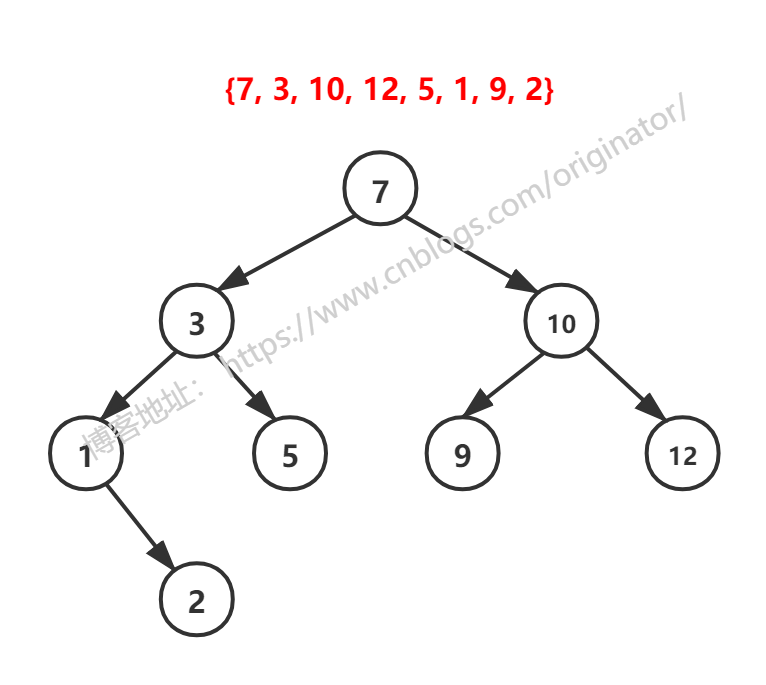
2、创建、添加、删除

　　创建和添加简单，删除情况比较复杂，有三种情况考虑：
　　①删除叶子结点（度为0），比如：2,5,9,12。
　　②删除只有左（右）孩子的结点（度为1），比如：1。
　　③删除有左（右）孩子的结点（度为2），比如：7,3,10。
　　删除度为2的结点，方法：取右子树的最小值替换它，且删除这个最小值。比如：删除7，用 7 的右子树最小值 9 替换7。且删除9。

　　代码示例：排序二叉树创建、添加、删除

// 二叉树
public class BinaryTree {
    // 根结点
    protected TreeNode root;

    /**
     * 获取树的高度
     *
     * @return
     */
    public int getHeight() {
        return this.getHeight(root);
    }

    protected int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        }

        final int left = this.getHeight(root.left);
        final int right = this.getHeight(root.right);

        return Math.max(left, right) + 1;
    }

    /**
     * 获取树的结点数
     *
     * @return
     */
    public int getSize() {
        return this.getSize(root);
    }

    private int getSize(TreeNode root) {
        if (root == null) {
            return 0;
        }

        final int left = this.getSize(root.left);
        final int right = this.getSize(root.right);

        return left + right + 1;
    }

    // 中序遍历
    public void infixOrder() {
        this.infixOrder(root);
    }

    private void infixOrder(TreeNode root) {
        if (root != null) {
            this.infixOrder(root.left);
            System.out.print("-->" + root.value);
            this.infixOrder(root.right);
        }
    }

    /**
     * 树结点结构
     */
    protected static class TreeNode {
        public int value;
        public TreeNode left;
        public TreeNode right;

        public TreeNode(int value) {
            this.value = value;
        }

        // 返回结点的度
        public int getDegree() {
            if (this.left == null && this.right == null) {
                return 0;
            }

            if ((this.left != null && this.right == null) || (this.left == null && this.right != null)) {
                return 1;
            }

            return 2;
        }

        @Override
        public String toString() {
            return "TreeNode{" +
                    "value=" + value +
                    '}';
        }
    }

}

public class BinarySortTree extends BinaryTree {

    public BinarySortTree() {

    }

    // arr = {7, 3, 10, 12, 5, 1, 9};
    public BinarySortTree(int[] arr) {
        if (arr == null || arr.length == 0) {
            return;
        }

        for (int i : arr) {
            this.add(i);
        }
    }

    /**
     * 添加结点
     *
     * @param value
     */
    public void add(int value) {
        TreeNode node = new TreeNode(value);

        if (root == null) {
            root = node;
            return;
        }

        this.add(root, node);
    }

    private void add(TreeNode root, TreeNode node) {
        if (node.value <= root.value) {
            if (root.left == null) {
                root.left = node;
            } else {
                this.add(root.left, node);
            }
        } else {
            if (root.right == null) {
                root.right = node;
            } else {
                this.add(root.right, node);
            }
        }
    }

    /**
     * 删除结点
     *
     * @param value
     */
    public void delNode(int value) {
        if (this.checkRoot(value)) {
            return;
        }

        // 1.查找要删除的结点
        final TreeNode targetNode = this.search(value);
        if (targetNode == null) {
            return;
        }

        this.delNode(targetNode);
    }

    private void delNode(TreeNode targetNode) {
        // 2.查找 targetNode 的父结点
        final int value = targetNode.value;
        final TreeNode parent = this.searchParent(value);

        // 度为0
        if (targetNode.getDegree() == 0) {
            if (parent.left != null && parent.left.value == value) {
                parent.left = null;
            } else if (parent.right != null && parent.right.value == value) {
                parent.right = null;
            }
        }
        // 度为1
        else if (targetNode.getDegree() == 1) {
            // 是左子结点
            if (targetNode.left != null) {
                if (parent.left.value == value) {
                    parent.left = targetNode.left;
                } else {
                    parent.right = targetNode.left;
                }
            } else {
                if (parent.left.value == value) {
                    parent.left = targetNode.right;
                } else {
                    parent.right = targetNode.right;
                }
            }
        }
        // 度为2
        else {
            targetNode.value = this.delRightTreeMin(targetNode.right);
        }

    }

    // 单独处理根结点
    private boolean checkRoot(int value) {
        if (root == null) {
            return true;
        }

        if (root.value == value) {
            if (root.getDegree() == 0) {
                root = null;
                return true;
            }

            if (root.getDegree() == 1) {
                if (root.left != null) {
                    root = root.left;
                } else {
                    root = root.right;
                }
                return true;
            }
        }

        return false;
    }

    private int delRightTreeMin(TreeNode node) {
        TreeNode temp = node;

        while (temp.left != null) {
            temp = temp.left;
        }

        this.delNode(temp);

        return temp.value;
    }

    /**
     * 查找指定结点 value
     *
     * @param value
     * @return
     */
    private TreeNode search(int value) {
        return this.search(root, value);
    }

    private TreeNode search(TreeNode root, int value) {
        if (root != null) {
            if (value == root.value) {
                return root;
            }

            // 递归左孩子
            if (value < root.value) {
                return this.search(root.left, value);
            } else {
                // 递归右孩子
                return this.search(root.right, value);
            }
        }

        return null;
    }

    /**
     * 查找指定结点 value 的父结点
     *
     * @param value
     * @return
     */
    private TreeNode searchParent(int value) {
        return this.searchParent(root, value);
    }

    private TreeNode searchParent(TreeNode root, int value) {
        if (root != null) {
            if ((root.left != null && root.left.value == value) ||
                    (root.right != null && root.right.value == value)) {
                return root;
            }

            // 递归左子树
            if (value < root.value) {
                return this.searchParent(root.left, value);
            } else {
                // 递归右子树
                return this.searchParent(root.right, value);
            }
        }

        return null;
    }

}

　　代码示例：测试类

public class Main {

    public static void main(String[] args) {
        // 1.创建
        int[] arr = {7, 3, 10, 12, 5, 1, 9};
        BinarySortTree sortTree = new BinarySortTree(arr);

        // 2.中序遍历
        sortTree.infixOrder();
        System.out.println("");

        // 3.添加
        sortTree.add(2);
        sortTree.infixOrder();
        System.out.println("");

        // 4.删除
        sortTree.delNode(10);
        sortTree.delNode(3);
        sortTree.delNode(9);
        sortTree.delNode(12);
        sortTree.delNode(1);
        sortTree.delNode(2);
        sortTree.delNode(5);
        //sortTree.delNode(7);
        sortTree.infixOrder();
    }
}

// 结果
-->1-->3-->5-->7-->9-->10-->12
-->1-->2-->3-->5-->7-->9-->10-->12
-->7

二、平衡二叉树（Self-balancing binary search tree ，AVL树）

1、介绍

　　给定一个数列，{1,2,3,4,5}，构建排序二叉树为：

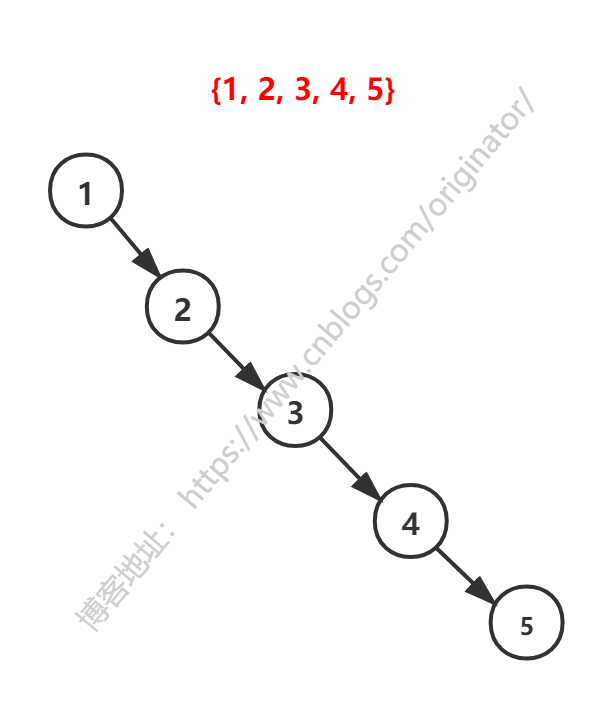
　　排序二叉树存在的问题：左子树都为空，从形式上看，像一个单链表；插入速度没有影响，查询速度明显降低（因为每次需要比较左子树），比单链表还慢。
　　解决：引入平衡二叉树。
　　定义：自平衡的排序二叉树。性质：左右两个子树的高度差绝对值不超过1，且左右子树也是平衡二叉树。
　　在平衡二叉树中插入结点要随时保证插入后整棵二叉树是平衡的，所以可能需要通过一次或多次旋转来重新平衡这个树。可以保证查询效率较高。
　　平衡二叉树是在排序二叉树的基础上定义的，所以，平衡二叉树是一颗排序二叉树。

2、左旋　　

　　右高，左旋

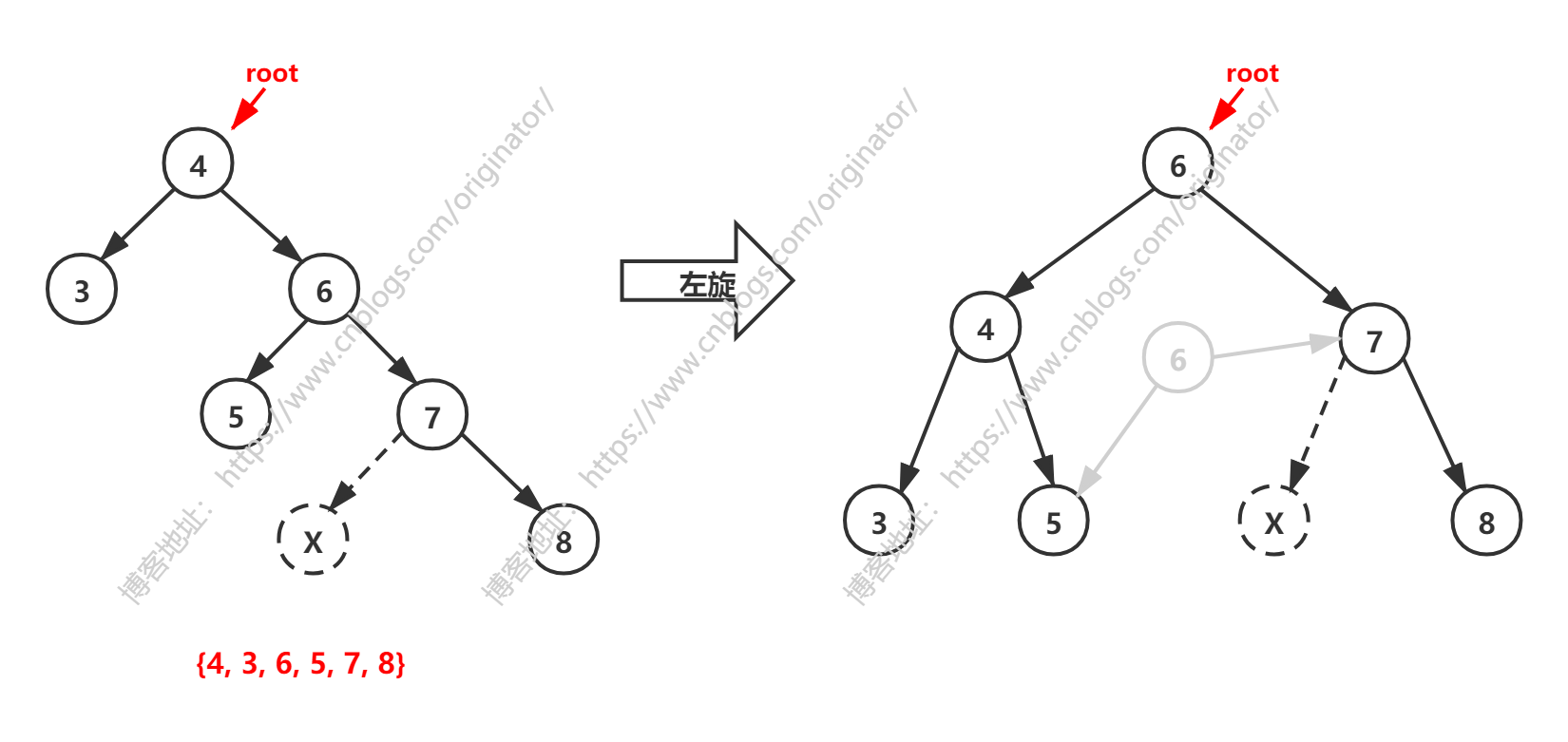
　　代码示例：对 root 左旋

// 左旋
private void leftRotate(TreeNode root) {
    TreeNode newNode = new TreeNode(root.value);
    newNode.left = root.left;
    newNode.right = root.right.left;

    root.value = root.right.value;
    root.left = newNode;
    root.right = root.right.right;
}

　　说明：root 的右子树高度 - 左子树高度 > 1，那么进行左旋。图示：X 结点，可能是 7 的左孩子或者右孩子。按上述方法左旋，都可以达到平衡。但是，如果 X 结点是 5 的左孩子或者右孩子，按上述方法就不能平衡，后面会介绍。
　　旋转后，原来的结点 6（灰色）其实还在，只是没有引用指向它，它会JVM视为垃圾回收掉。

3、右旋

　　左高，右旋

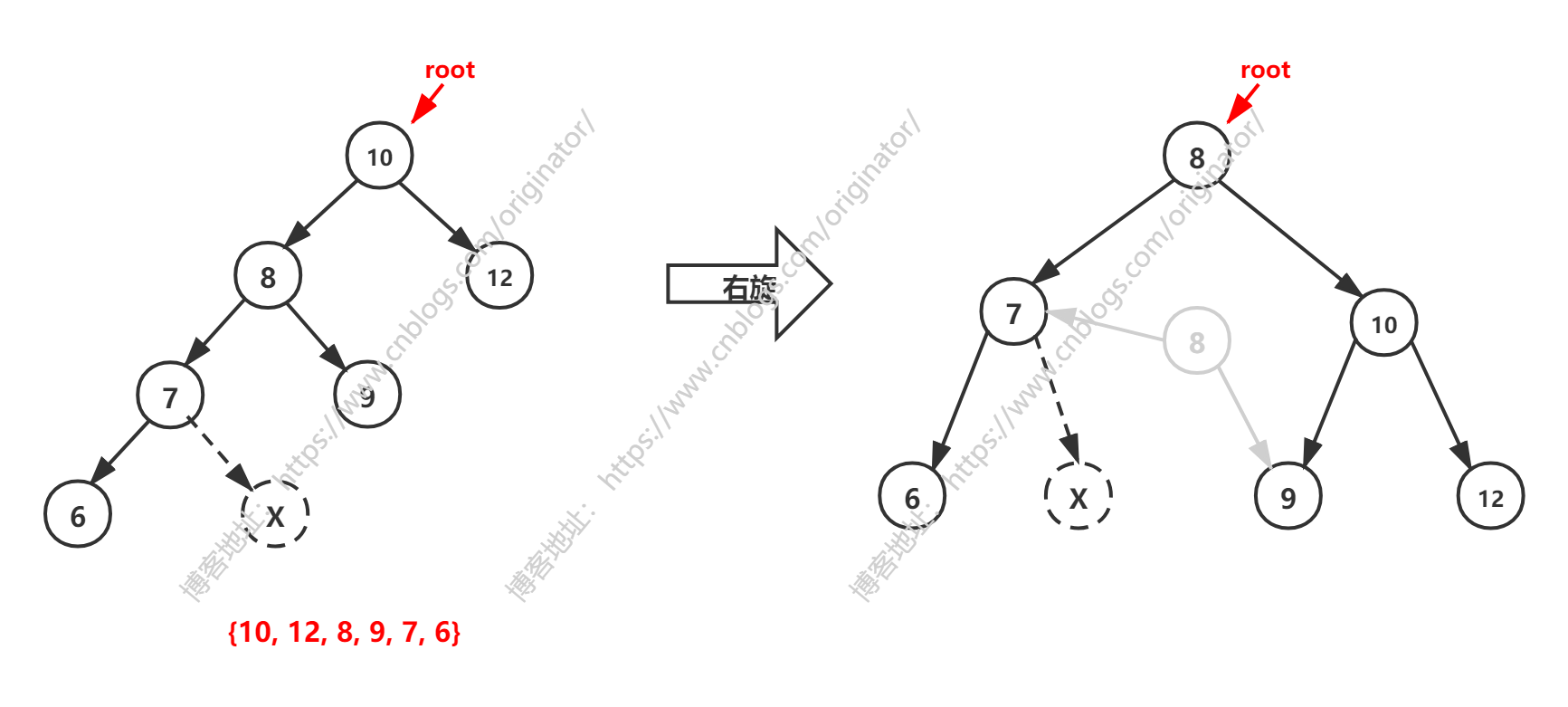
　　代码示例：对 root 右旋

// 右旋
private void rightRotate(TreeNode root) {
    TreeNode newNode = new TreeNode(root.value);
    newNode.left = root.left.right;
    newNode.right = root.right;

    root.value = root.left.value;
    root.left = root.left.left;
    root.right = newNode;
}

　　说明：与左旋同理。

4、双旋

　　左旋问题：
　　上面提到，"如果 X 结点是 5 的左孩子或者右孩子，按上述方法就不能平衡。"，如图所示：

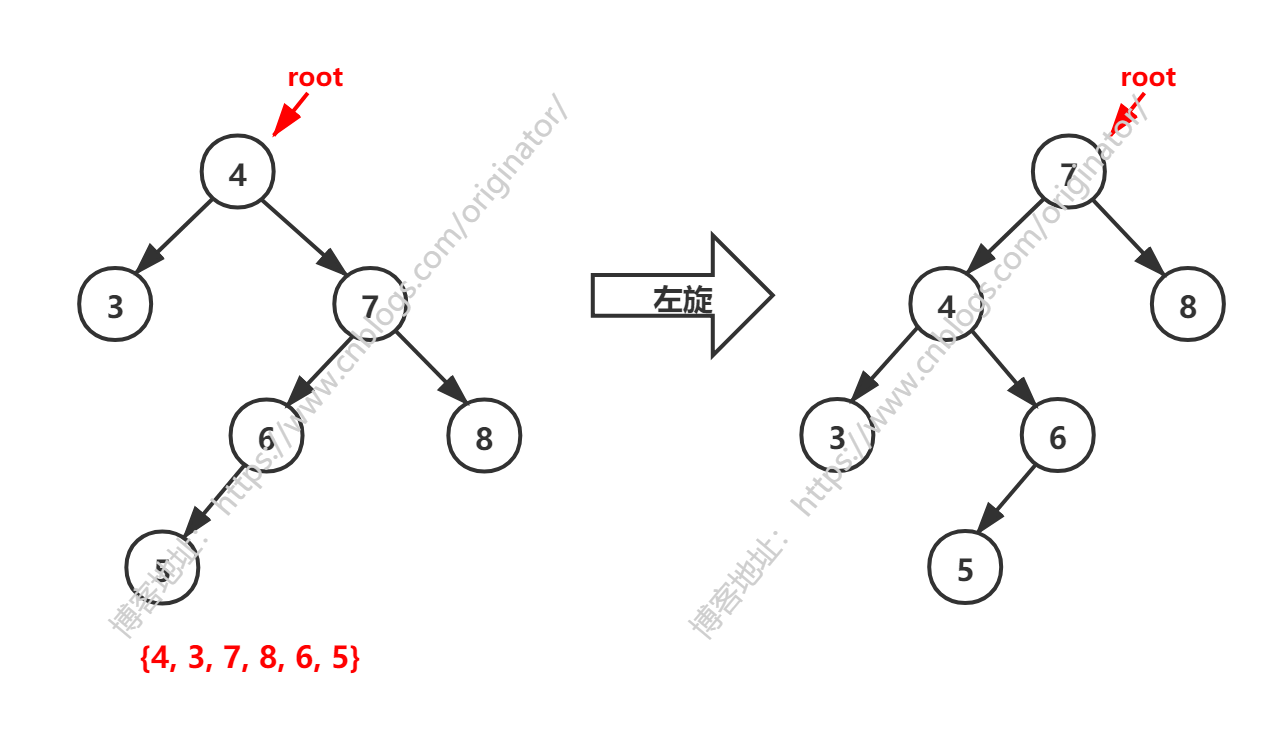
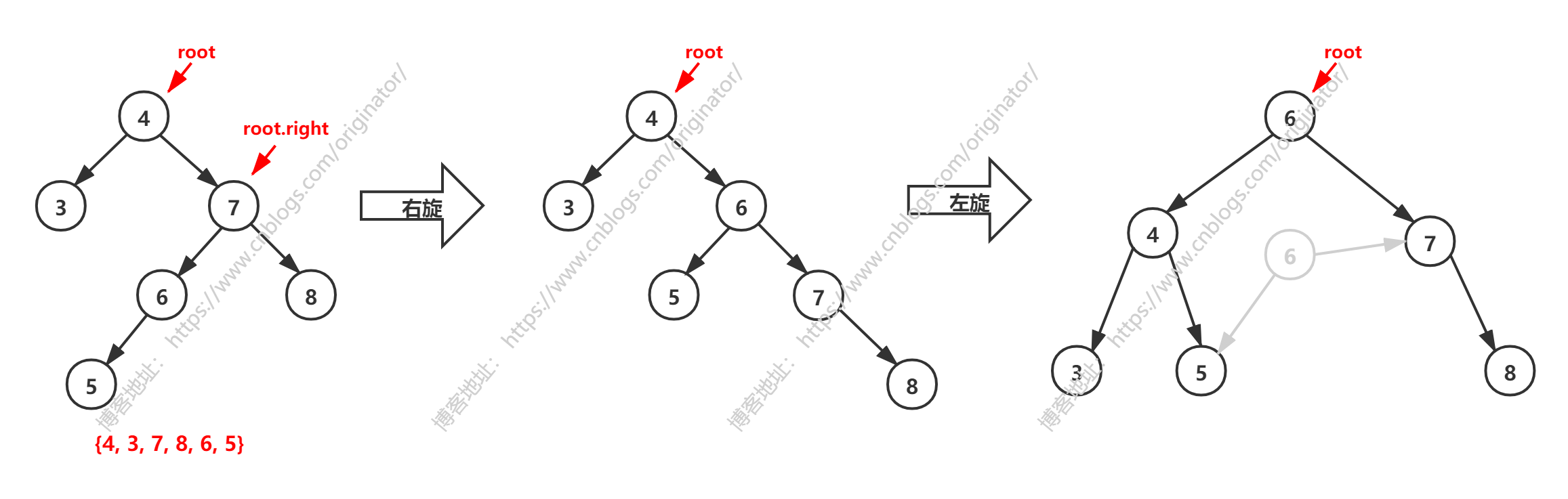
　　经过左旋后，发现树并没有平衡。解决办法：
　　①先 root.right 右旋（因为对于root.right是左子树高度 > 右子树）。
　　②再对 root 左旋。

　　右旋问题：
　　同理：

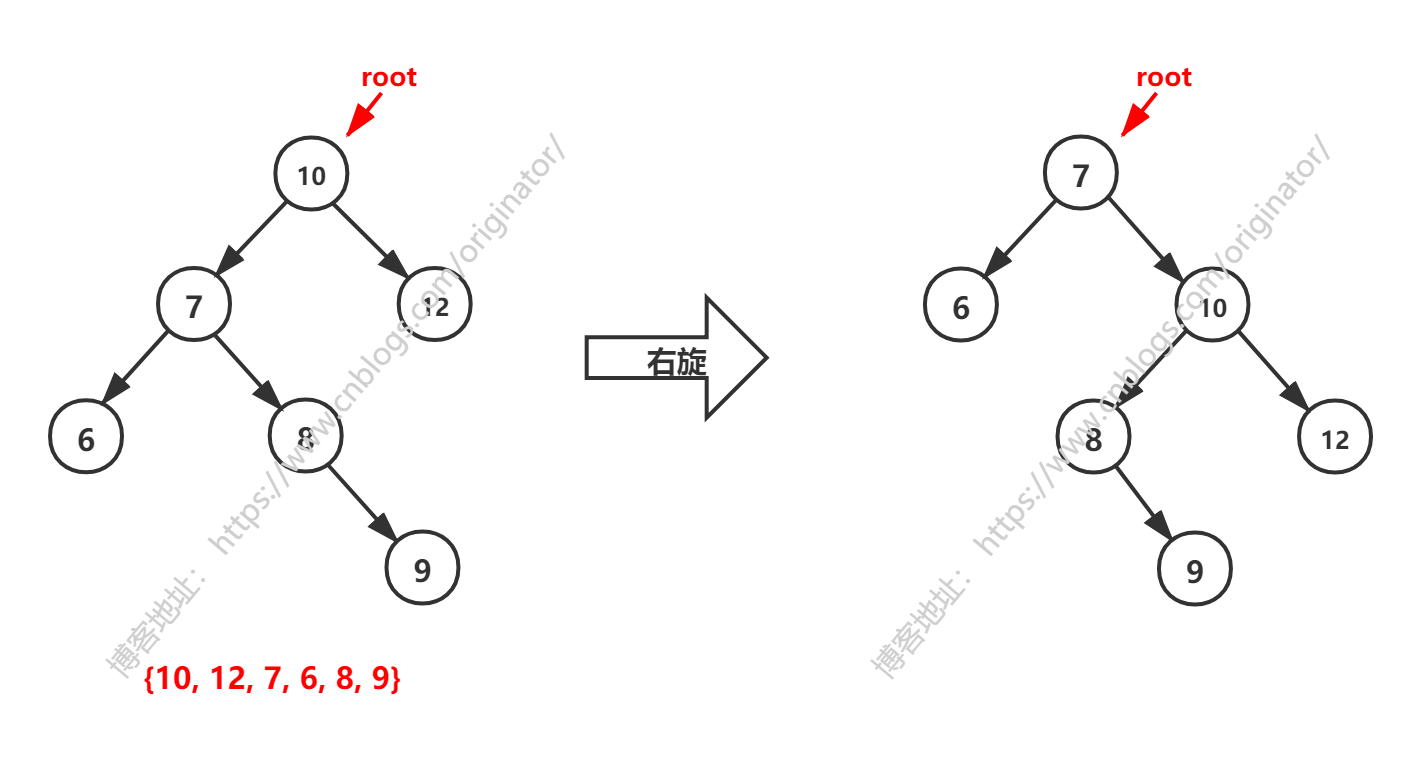
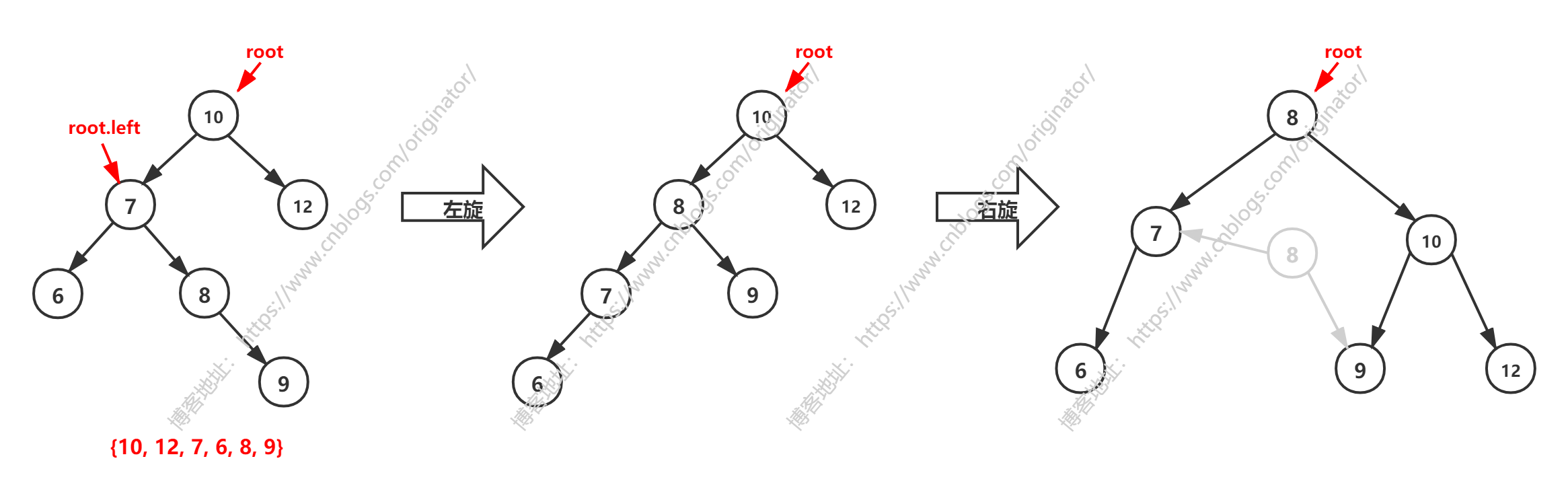
　　经过右旋后，发现树并没有平衡。解决办法：
　　①先 root.left 左旋（因为对于root.left是右子树高度 > 左子树）。
　　②再对 root 右旋。

5、代码实现

　　代码示例：平衡二叉树

public class AVLTree extends BinarySortTree {

    public AVLTree() {
    }

    public AVLTree(int[] arr) {
        super(arr);
    }

    /**
     * 复写add方法，在排序二叉树性质上，需要调整树的平衡
     *
     * @param value
     */
    @Override
    public void add(int value) {
        // 1.添加结点
        super.add(value);

        // 2.检查是否平衡.如果（右子树高度 - 左子树 > 1）,左旋
        if (this.getHeight(root.right) - this.getHeight(root.left) > 1) {
            // 右.左子树高度 > 右.右子树
            if (this.getHeight(root.right.left) > this.getHeight(root.right.right)) {
                // 右子树->右旋
                rightRotate(root.right);
            }

            leftRotate(root);
        }

        // 2.检查是否平衡.如果（左子树高度 - 右子树 > 1）,右旋
        if (this.getHeight(root.left) - this.getHeight(root.right) > 1) {
            // 左.右子树高度 > 左.左子树
            if (this.getHeight(root.left.right) > this.getHeight(root.left.left)) {
                // 左子树->左旋
                leftRotate(root.left);
            }

            rightRotate(root);
        }
    }

    // 左旋
    private void leftRotate(TreeNode root) {
        TreeNode newNode = new TreeNode(root.value);
        newNode.left = root.left;
        newNode.right = root.right.left;

        root.value = root.right.value;
        root.left = newNode;
        root.right = root.right.right;
    }

    // 右旋
    private void rightRotate(TreeNode root) {
        TreeNode newNode = new TreeNode(root.value);
        newNode.left = root.left.right;
        newNode.right = root.right;

        root.value = root.left.value;
        root.left = root.left.left;
        root.right = newNode;
    }

}

　　代码示例：测试类

public class Main {
    public static void main(String[] args) {
        // int[] arr = {4, 3, 6, 5, 7, 8};
        // int[] arr = {10, 12, 8, 9, 7, 6};
        // int[] arr = {4, 3, 7, 8, 6, 5};
        int[] arr = {10, 12, 7, 6, 8, 9};

        AVLTree avlTree = new AVLTree(arr);

        avlTree.infixOrder();
    }
}

三、多路查找树（multi-way search tree）

1、介绍

　　二叉树的问题，二叉树需要加载到内存，如果结点少，没有什么问题，但是如果二叉树的结点很多（比如1亿），就存在如下问题：
　　问题1：在构建二叉树时，需要多次进行I/O操作（海量数据存在数据库或文件中），结点海量，构建二叉树时，速度有影响。
　　问题2：结点海量，也会造成二叉树的高度很大，降低操作速度。

2、2-3树

　　在二叉树中，每个结点有数据项，最多有两个子结点。如果允许每个结点可以有更多的数据项和更多的子结点，就是多叉树（multiway tree）。2-3树，2-3-4树就是多叉树，多叉树通过重新组织结点，减少树的高度，能对二叉树进行优化。如图：

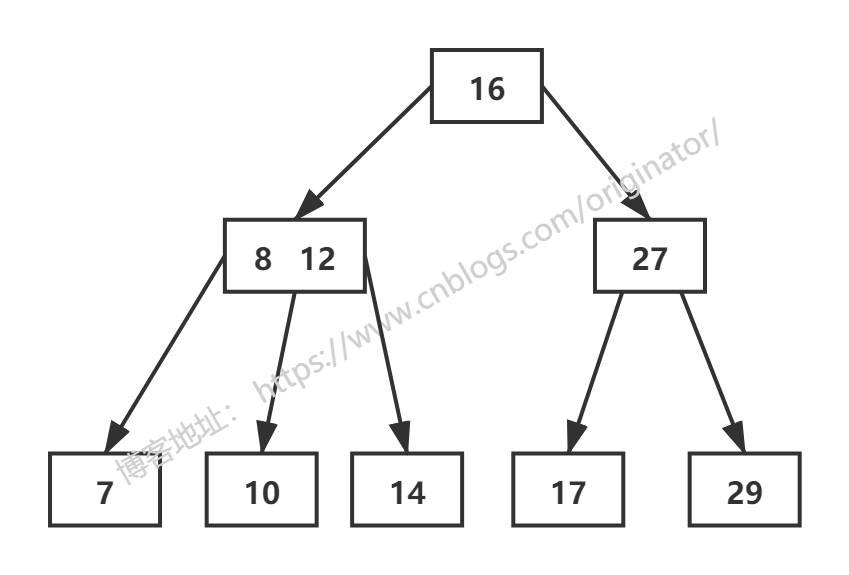
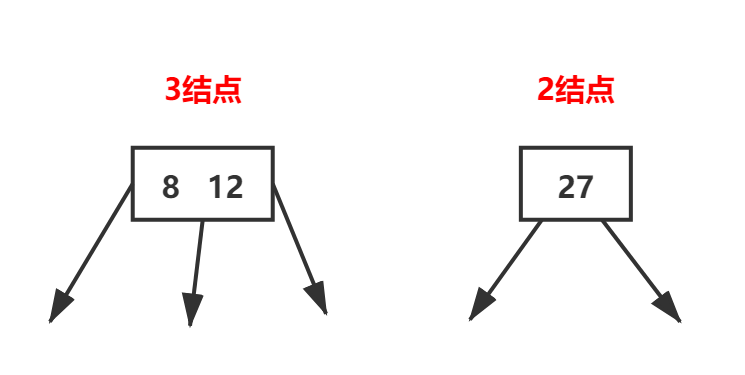
　　多路查找树中的每一个结点都具有两个孩子或者三个孩子，我们称之为2-3树。是一种平衡的多路查找树。2-3树，2-3-4树是B树的一个特例，属于B树。2-3树，高度平衡。
　　一个结点拥有两个孩子和一个元素称之为2结点，它跟二叉排序树类似，左子树包含的元素小于结点的元素，小于右子树包含的元素。
　　不同的是，这个2结点要么没有孩子，要么有两个孩子。不能只有一个孩子。
　　2-3树所有叶子都在同一层次。

3、2-3-4树

　　概念和2-3树类似，也是一种B树。

四、B树（B-树）

1、介绍

　　B树通过重新组织结点，降低树的高度，减少I/O读写次数来提升效率。文件系统及数据库系统的设计者利用了磁盘预读原理，将一个结点的大小设为等于一页（页得大小通常为4k），这样每个结点只需要一次I/O就可以完全载入。
　　将树的度M设置为1024，在600亿个元素中最多只需要4次I/O操作就可以读取到想要的元素，B树（B+）广泛应用于文件存储系统以及数据库系统中。
　　所有叶子结点都在同一层。

2、结构

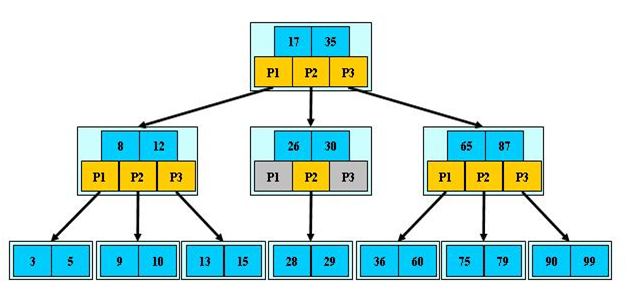
　　B树的阶：节点的最多子节点个数。比如2-3树的阶是3，2-3-4树的阶是4
　　B树的搜索：从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为空，或已经是叶子结点。关键字集合分布在整颗树中，即叶子节点和非叶子节点都存放数据。搜索有可能在非叶子结点结束。其搜索性能等价于在关键字全集内做一次二分查找。
　　B树的插入算法中，通过结点的向上"分裂"，代替了专门的平衡调整。

五、B+树

1、介绍

　　B+树是B树的变体，也是一种多路搜索树。

2、结构

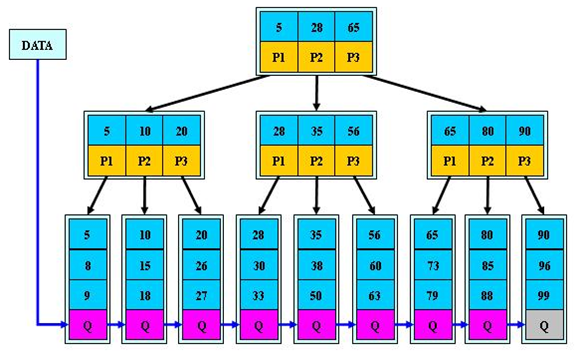
　　B+树的搜索：与B树基本相同，区别是B+树只有达到叶子结点才命中（B树可以在非叶子结点命中），其性能也等价于在关键字全集做一次二分查找。所有关键字都出现在叶子结点的链表中（即数据只能在叶子节点【也叫稠密索引】），且链表中的关键字恰好是有序的。
　　不可能在非叶子结点命中。
　　非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储（关键字）数据的数据层。
　　更适合文件索引系统。
　　B树和B+树各有自己的应用场景，不能说B+树完全比B树好，反之亦然。

六、B*树

1、介绍

　　B*树是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针。

2、结构

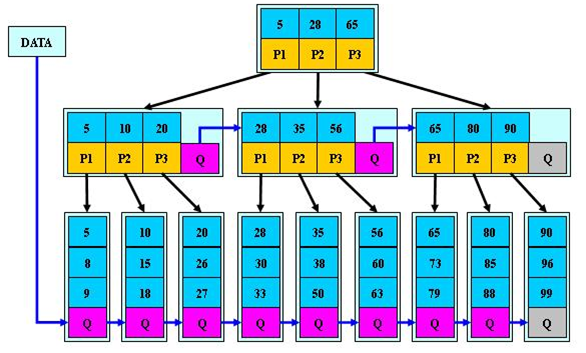
　　B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3，而B+树的块的最低使用率为B+树的1/2。
　　B*树分配新结点的概率比B+树要低，空间使用率更高。