数据结构与算法(三)——栈
一、栈
1、介绍
栈是一种先进后出的线性表,它要求只能在表尾(栈顶)进行插入和删除操作。可以用数组或链表来实现,一般用顺序表来实现。
栈的应用:
①子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中。
②处理递归调用:和子程序的调用类似,只是除了储存下一个指令的地址外,也将参数、区域变量等数据存入堆栈中。
③表达式的转换(中缀表达式转后缀表达式)与求值(实际解决)。
④二叉树的遍历。
⑤图的深度优先(depth一first)搜索。
2、栈的顺序存储实现
顾名思义,用顺序表的方法实现,通常用数组。栈的顺序存储结构:
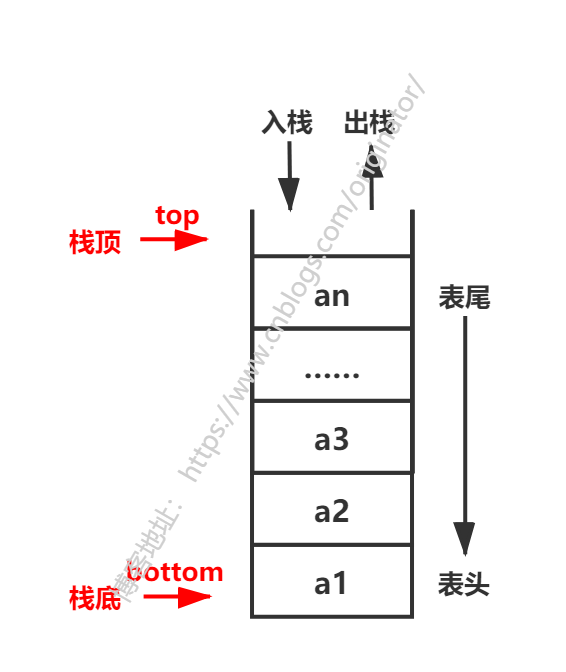
代码示例:数组实现栈

1 // 用数组实现栈 2 public class MyStack<T> { 3 private T[] elementData; 4 // 栈顶指针 5 private int top; 6 7 public MyStack(int initialCapacity) { 8 elementData = (T[]) new Object[initialCapacity]; 9 top = 0; 10 } 11 12 // 入栈 13 public T push(T item) { 14 if (isFull()) { 15 throw new RuntimeException("堆栈溢出~"); 16 } 17 18 elementData[top] = item; 19 top++; 20 21 return item; 22 } 23 24 // 出栈 25 public T pop() { 26 if (empty()) { 27 return null; 28 } 29 30 top--; 31 return elementData[top]; 32 } 33 34 // 读取栈顶元素 35 public T peek() { 36 if (empty()) { 37 return null; 38 } 39 40 return elementData[top - 1]; 41 } 42 43 // 判空 44 public boolean empty() { 45 return top == 0; 46 } 47 48 // 判满 49 private boolean isFull() { 50 return top == elementData.length; 51 } 52 53 // 栈的元素个数 54 public int size() { 55 int count = 0; 56 for (int i = top - 1; i >= 0; i++) { 57 count++; 58 } 59 return count; 60 } 61 62 @Override 63 public String toString() { 64 if (empty()) { 65 return "[]"; 66 } 67 68 StringBuilder builder = new StringBuilder(); 69 builder.append("["); 70 for (int i = top - 1; i >= 0; i--) { 71 builder.append(elementData[i]) 72 .append(","); 73 } 74 75 // 去掉最后一个, 76 builder.deleteCharAt(builder.length() - 1); 77 builder.append("]"); 78 79 return builder.toString(); 80 } 81 }
代码示例:测试类

1 // 测试类 2 public class Main { 3 public static void main(String[] args) { 4 MyStack<Integer> stack = new MyStack<>(5); 5 6 // 压栈 7 stack.push(9); 8 stack.push(5); 9 stack.push(2); 10 stack.push(7); 11 12 while (!stack.empty()) { 13 // 从栈顶弹出一个.会删除元素 14 System.out.println(stack.pop()); 15 } 16 17 // 从栈顶弹出一个.不会删除元素 18 // stack.peek(); 19 // System.out.println(stack); 20 } 21 } 22 23 // 结果 24 7 2 5 9
3、栈的链式存储实现
顾名思义,用链表的方法实现,通常用单链表。栈的链式储存结构:

代码示例:单链表(不带头结点)实现栈

1 public class MyLinkedStack<E> { 2 3 // 头指针 4 private Node<E> head; 5 6 public MyLinkedStack() { 7 8 } 9 10 // 入栈 11 public E push(E item) { 12 final Node<E> node = new Node<>(item); 13 14 node.next = head; 15 head = node; 16 17 return item; 18 } 19 20 // 出栈 21 public E pop() { 22 final Node<E> temp = head; 23 24 if (temp == null) { 25 return null; 26 } 27 28 head = head.next; 29 return temp.item; 30 } 31 32 // 读取栈顶元素 33 public E peek() { 34 if (head == null) { 35 return null; 36 } 37 38 return head.item; 39 } 40 41 // 判空 42 public boolean empty() { 43 return head == null; 44 } 45 46 // 栈的元素个数 47 public int size() { 48 int size = 0; 49 50 Node<E> temp = head; 51 while (temp != null) { 52 size++; 53 temp = temp.next; 54 } 55 56 return size; 57 } 58 59 @Override 60 public String toString() { 61 Node<E> temp = head; 62 63 if (temp == null) { 64 return "[]"; 65 } 66 67 StringBuilder builder = new StringBuilder(); 68 builder.append("["); 69 70 while (temp != null) { 71 builder.append(temp.item) 72 .append(","); 73 74 temp = temp.next; 75 } 76 77 // 去掉最后一个, 78 builder.deleteCharAt(builder.length() - 1); 79 builder.append("]"); 80 81 return builder.toString(); 82 } 83 84 private static class Node<E> { 85 public E item; 86 87 public Node<E> next; 88 89 public Node(E item) { 90 this.item = item; 91 } 92 93 } 94 }
代码示例:测试类

1 // 测试类 2 public static void main(String[] args) { 3 MyLinkedStack<Integer> stack = new MyLinkedStack<>(); 4 // 压栈 5 stack.push(9); 6 stack.push(5); 7 stack.push(2); 8 stack.push(7); 9 10 while (!stack.empty()) { 11 // 从栈顶弹出一个.会删除元素 12 System.out.println(stack.pop()); 13 } 14 } 15 16 // 结果 17 7 2 5 9
4、前缀、中缀、后缀表达式
中缀表达式:(3 + 4)* 5 - 16
前缀表达式(波兰表达式):- * + 3 4 5 16
后缀表达式(逆波兰表达式):3 4 + 5 * 16 -
①计算前缀表达式:"- * + 3 4 5 16"
计算流程图:注:这里仅支持多位整数计算。
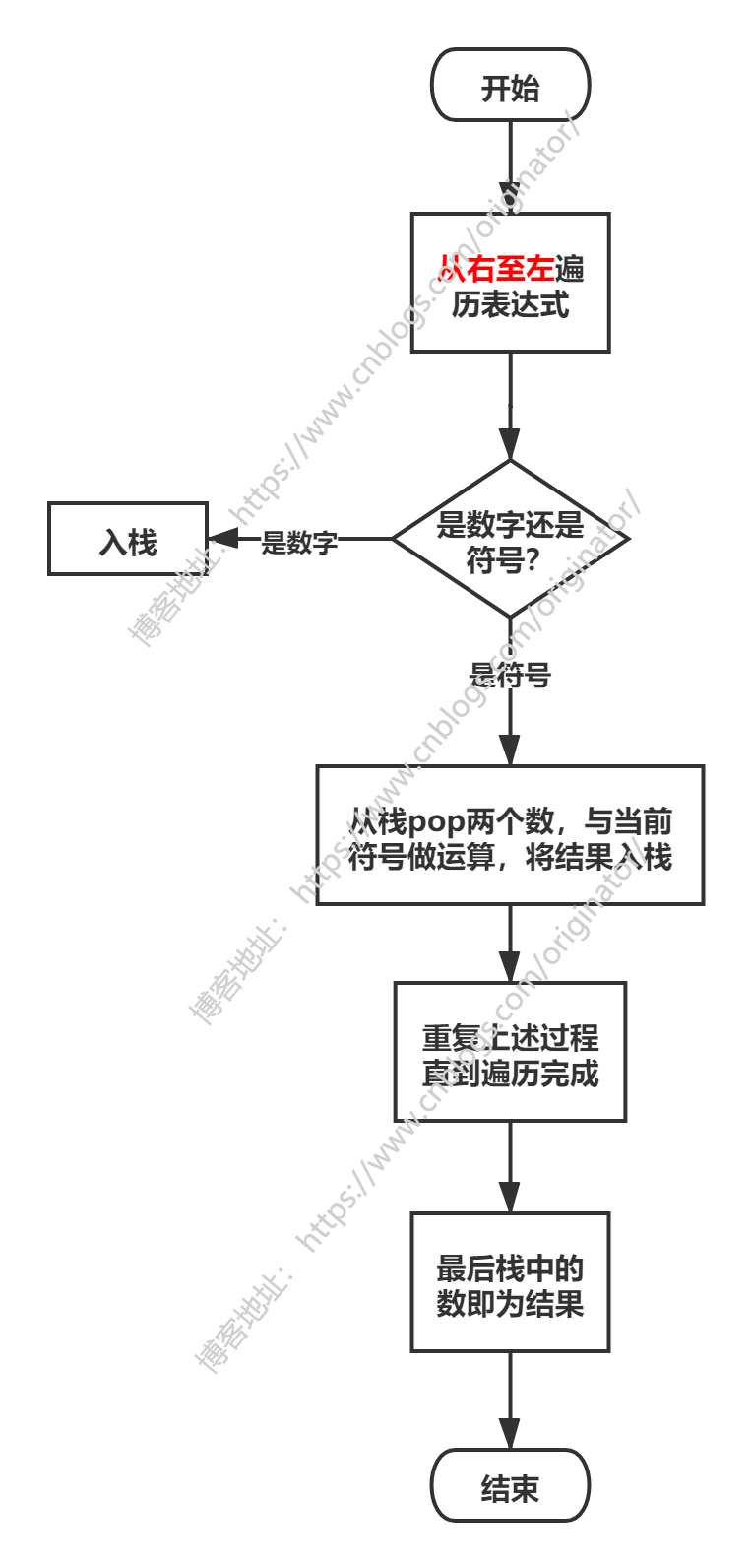
代码示例:见【类Poland】
②计算中缀表达式:"31+3 /1 -21"
计算流程图:创建两个栈,一个数栈,一个符号栈。注:这里仅支持多位整数计算,且不支持括号。
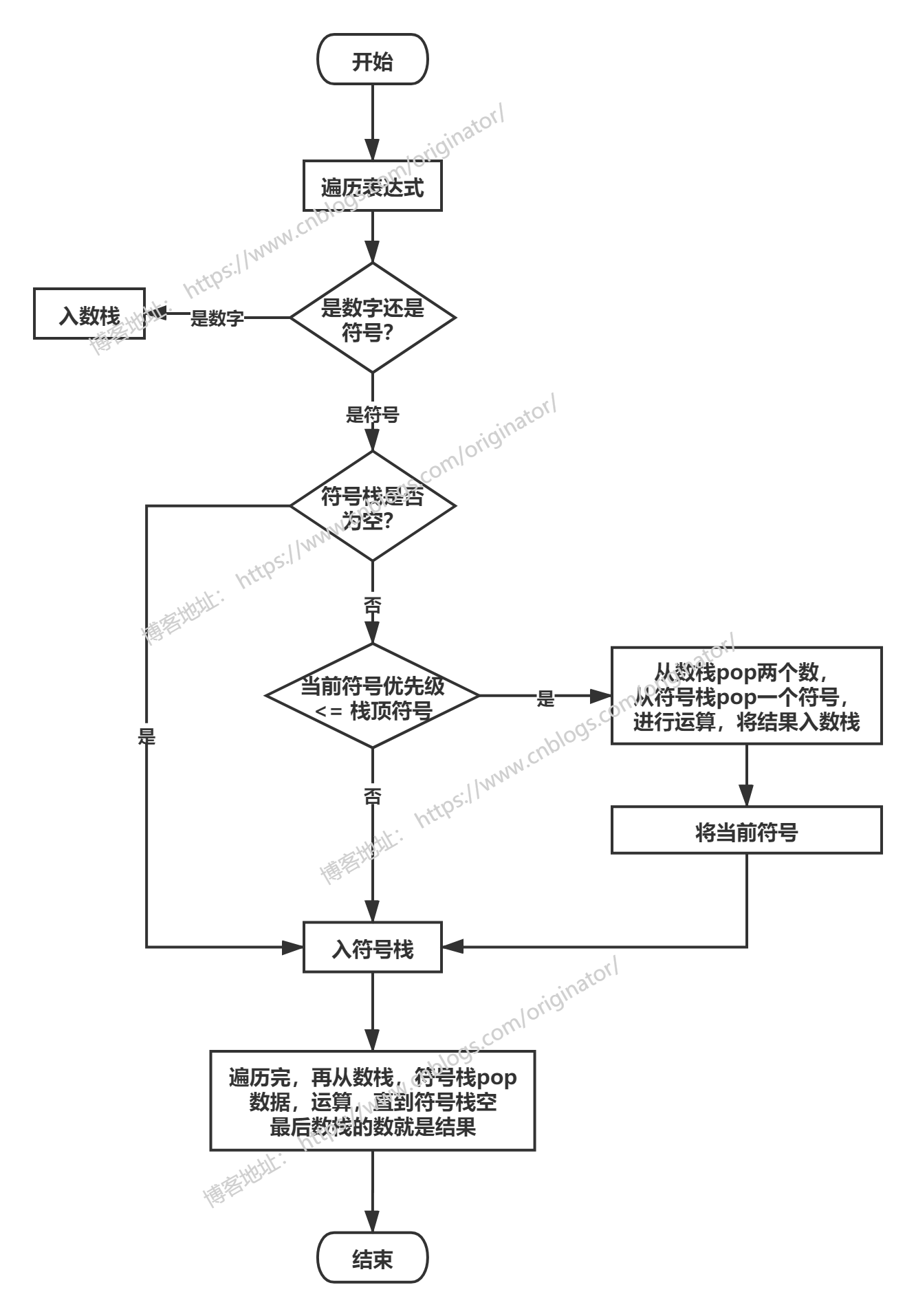
代码示例:见【类Poland】
③计算后缀表达式:"11 2 3 + 4 * + 5 -"
计算流程图:注:这里仅支持多位整数计算。
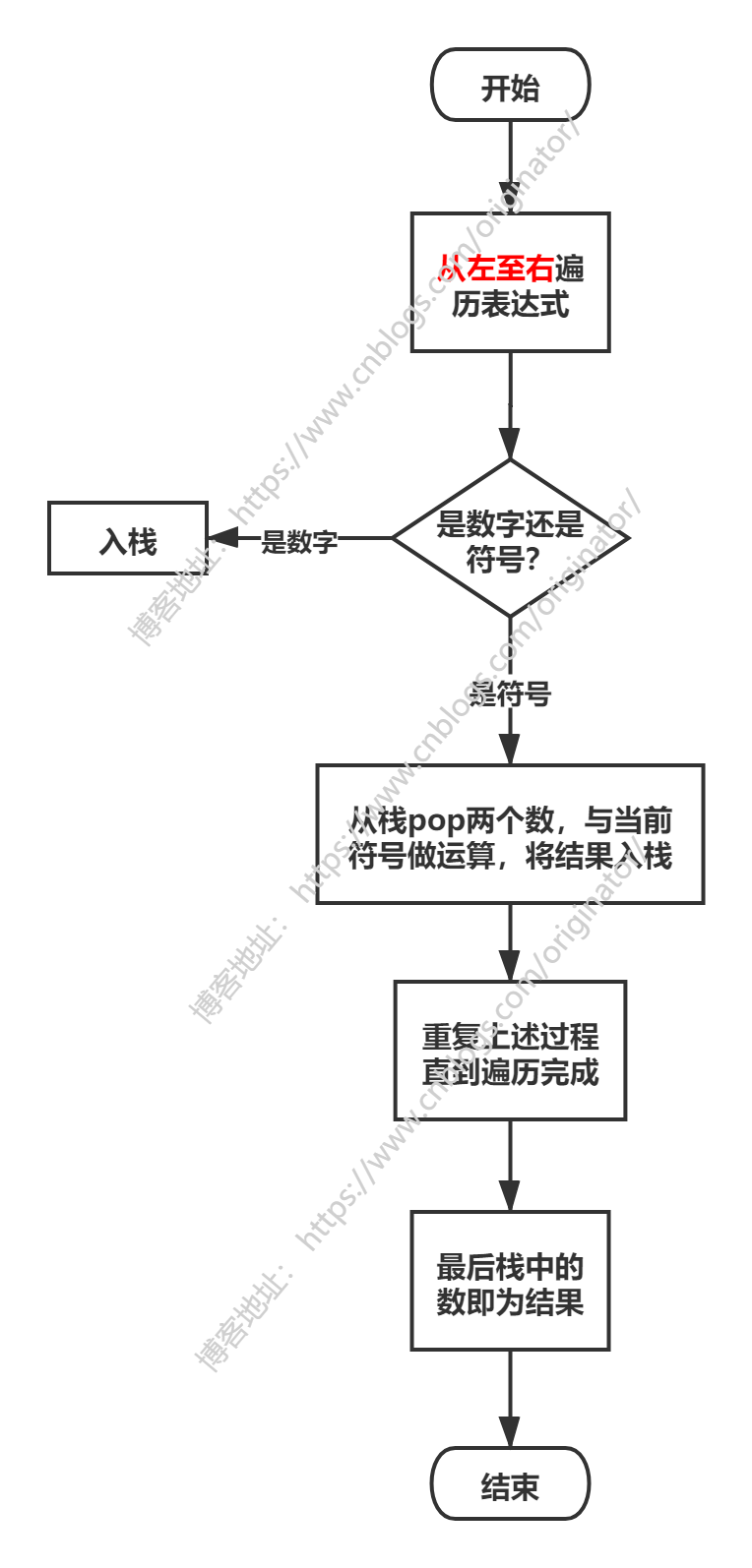
代码示例:见【类Poland】
前缀和后缀计算流程的区别:①遍历表达式方向不同;②弹栈出来的运算符号先后不同,一个a - b,一个b - a。
④中缀转后缀:
流程图:创建一个栈 stack 和一个结果存储list。注:仅支持整数和括号。
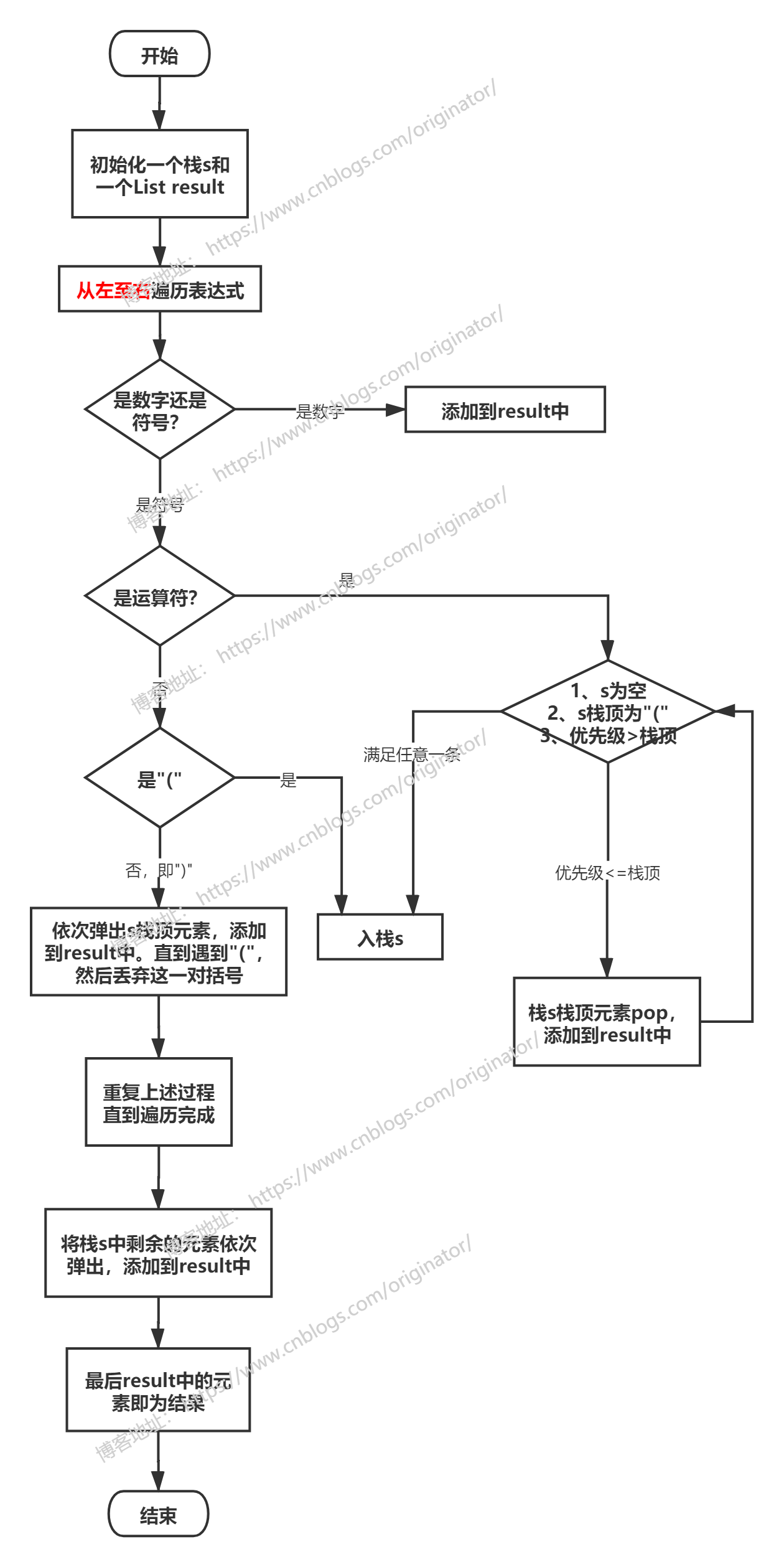
代码示例:见【类Poland】
代码示例:Poland

1 // 前缀、中缀、后缀表达式 2 public class Poland { 3 4 /** 5 * 匹配整数或小数 6 */ 7 private static final Pattern NUM_PATTERN = Pattern.compile("^(\\-|\\+)?\\d+(\\.\\d+)?$"); 8 9 /** 10 * 中缀表达式转后缀表达式 11 * 12 * @param infixExpression 11+((2+3) * 4) - 5 13 * @return 11 2 3 + 4 * + 5 - 14 */ 15 public static String toSuffixExpression(String infixExpression) { 16 infixExpression = infixExpression.replace(" ", ""); 17 18 Stack<String> stack = new Stack<>(); 19 List<String> result = new ArrayList<>(); 20 21 StringBuilder builder = new StringBuilder(); 22 // 1.遍历 23 for (int i = 0; i < infixExpression.length(); i++) { 24 final char c = infixExpression.charAt(i); 25 26 // ①.数,就直接添加到result.注意:可能是多位数 27 if (isNum(c)) { 28 builder.append(c); 29 30 // 可能会越界.有下一个且下一个是数 31 if (i != infixExpression.length() - 1 && isNum(infixExpression.charAt(i + 1))) { 32 continue; 33 } 34 35 result.add(builder.toString()); 36 37 // 清空 builder 38 builder.delete(0, builder.length()); 39 } else if (c == '(') { 40 stack.push(String.valueOf(c)); 41 } else if (c == ')') { 42 // stack依次出栈添加到result中直到遇到'(' 43 while (!"(".equals(stack.peek())) { 44 result.add(stack.pop()); 45 } 46 47 // 将'('弹出,消除这对括号 48 stack.pop(); 49 } else { 50 // ②.是运算符 51 while (!stack.empty() && !"(".equals(stack.peek()) && priority(String.valueOf(c), stack.peek()) <= 0) { 52 result.add(stack.pop()); 53 } 54 55 // 将c压栈 56 stack.push(String.valueOf(c)); 57 } 58 } 59 60 // 2.尾处理.将stack中剩余的运算符依次弹出加入result 61 while (!stack.empty()) { 62 result.add(stack.pop()); 63 } 64 65 // 3.此时result已是中缀表达式.用String输出 66 for (String s : result) { 67 builder.append(s) 68 .append(" "); 69 } 70 // 去除最后一个空格 71 if (builder.toString().length() != 0) { 72 builder.deleteCharAt(builder.length() - 1); 73 } 74 75 return builder.toString(); 76 } 77 78 // 计算前缀表达式(波兰表达式) 79 public static double calculatePrefix(String prefixExpression) { 80 final String[] list = prefixExpression.split(" "); 81 82 Stack<String> stack = new Stack<>(); 83 for (int i = list.length - 1; i >= 0; i--) { 84 if (isNum(list[i])) { 85 stack.push(list[i]); 86 } else { 87 final double num1 = Double.parseDouble(stack.pop()); 88 final double num2 = Double.parseDouble(stack.pop()); 89 90 stack.push(String.valueOf(cal(num2, num1, list[i]))); 91 } 92 } 93 94 // 最后stack中的数据是运算结果 95 return Double.parseDouble(stack.pop()); 96 } 97 98 // 计算中缀表达式 99 public static double calculateInfix(String infixExpression) { 100 infixExpression = infixExpression.replace(" ", ""); 101 102 MyStack<Double> numStack = new MyStack<>(20); 103 MyStack<Character> operStack = new MyStack<>(20); 104 105 StringBuilder builder = new StringBuilder(); 106 for (int i = 0; i < infixExpression.length(); i++) { 107 final char c = infixExpression.charAt(i); 108 109 if (!isOper(c)) { 110 // 数,注意:可能是多位数 111 builder.append(c); 112 113 // 可能会越界.有下一个且下一个是数 114 if (i != infixExpression.length() - 1 && !isOper(infixExpression.charAt(i + 1))) { 115 continue; 116 } 117 118 numStack.push(Double.parseDouble(builder.toString())); 119 120 // 清空 builder 121 builder.delete(0, builder.length()); 122 } else { 123 // 符号 124 if (!operStack.empty() && priority(c, operStack.peek()) <= 0) { 125 // 注意顺序 126 final double num1 = numStack.pop(); 127 final double num2 = numStack.pop(); 128 129 final double cal = cal(num1, num2, operStack.pop()); 130 numStack.push(cal); 131 } 132 133 // 将当前符号入栈 134 operStack.push(c); 135 } 136 } 137 138 while (!operStack.empty()) { 139 final double num1 = numStack.pop(); 140 final double num2 = numStack.pop(); 141 142 final double cal = cal(num1, num2, operStack.pop()); 143 numStack.push(cal); 144 } 145 146 return numStack.pop(); 147 } 148 149 // 计算后缀表达式(逆波兰表达式) 150 public static double calculateSuffix(String suffixExpression) { 151 final String[] list = suffixExpression.split(" "); 152 153 Stack<String> stack = new Stack<>(); 154 for (String s : list) { 155 if (isDecimal(s)) { 156 stack.push(s); 157 } else { 158 final double num1 = Double.parseDouble(stack.pop()); 159 final double num2 = Double.parseDouble(stack.pop()); 160 161 stack.push(String.valueOf(cal(num1, num2, s))); 162 } 163 } 164 165 // 最后stack中的数据是运算结果 166 return Double.parseDouble(stack.pop()); 167 } 168 169 /** 170 * 计算 171 * 172 * @param num1 数1 173 * @param num2 数2 174 * @param oper 运算符 175 * @return 176 */ 177 private static double cal(double num1, double num2, char oper) { 178 double res = 0; 179 switch (oper) { 180 case '+': 181 res = num1 + num2; 182 break; 183 case '-': 184 res = num2 - num1; 185 break; 186 case '*': 187 res = num1 * num2; 188 break; 189 case '/': 190 res = num2 / num1; 191 break; 192 default: 193 break; 194 } 195 return res; 196 } 197 198 private static double cal(double num1, double num2, String oper) { 199 return cal(num1, num2, oper.charAt(0)); 200 } 201 202 /** 203 * 判断是不是数字 int double long float 204 */ 205 private static boolean isDecimal(String s) { 206 return NUM_PATTERN.matcher(s).matches(); 207 } 208 209 /** 210 * 判断是不是数字 211 * 212 * @param val 213 * @return 214 */ 215 private static boolean isNum(String val) { 216 return val.matches("\\d+"); 217 } 218 219 /** 220 * 判断是不是数字 221 * 222 * @param val 223 * @return 224 */ 225 private static boolean isNum(char val) { 226 // '0'[48] -> '9'[57] 227 return val >= 48 && val <= 57; 228 } 229 230 /** 231 * 判断是不是一个运算符 232 * 233 * @param val 234 * @return 235 */ 236 private static boolean isOper(char val) { 237 return val == '+' || val == '-' || val == '*' || val == '/'; 238 } 239 240 /** 241 * 判断是不是一个符号 242 * 243 * @param val 244 * @return 245 */ 246 private static boolean isSymbol(char val) { 247 return isOper(val) || val == '(' || val == ')'; 248 } 249 250 /** 251 * 比较两个符号的优先级 252 * 253 * @param oper1 符号1 + - * / 254 * @param oper2 符号2 255 * @return 1:符号1>符号2 ; 0:符号1=符号2 ; -1:符号1<符号2 256 */ 257 public static int priority(char oper1, char oper2) { 258 if (oper1 == '*' || oper1 == '/') { 259 if (oper2 == '*' || oper2 == '/') { 260 return 0; 261 } 262 return 1; 263 } 264 265 // oper1 = + - 266 if (oper2 == '*' || oper2 == '/') { 267 return -1; 268 } 269 return 0; 270 } 271 272 /** 273 * 比较两个符号的优先级 274 * 275 * @param oper1 符号1 + - * / 276 * @param oper2 符号2 277 * @return 1:符号1>符号2 ; 0:符号1=符号2 ; -1:符号1<符号2 278 */ 279 public static int priority(String oper1, String oper2) { 280 return priority(oper1.charAt(0), oper2.charAt(0)); 281 } 282 283 }
代码示例:测试类

1 // 测试类 2 public static void main(String[] args) { 3 // 1.计算前缀表达式: (3+4)×5-16=19 4 final double v = Poland.calculatePrefix("- * + 3 4 5 16"); 5 System.out.println("计算前缀表达式的结果是:" + v); 6 7 // 2.计算中缀表达式: 31+3 /1 -21=13 (仅支持多位整数计算,且不支持括号) 8 final double v1 = Poland.calculateInfix("31+3 /1 -21"); 9 System.out.println("计算中缀表达式的结果是:" + v1); 10 11 // 3.中 转 后 12 String infixExpression = "11+( (2+3) * 4) - 5"; 13 System.out.println("中缀表达式:" + infixExpression); 14 final String suffixExpression = Poland.toSuffixExpression(infixExpression); 15 System.out.println("中转后:" + suffixExpression); 16 17 // 4.计算后缀表达式: 11+( (2+3) * 4) - 5=26 18 final double v2 = Poland.calculateSuffix(suffixExpression); 19 System.out.println("计算后缀表达式的结果是:" + v2); 20 } 21 22 // 结果 23 计算前缀表达式的结果是:19.0 24 计算中缀表达式的结果是:13.0 25 中缀表达式:11+( (2+3) * 4) - 5 26 中转后:11 2 3 + 4 * + 5 - 27 计算后缀表达式的结果是:26.0
5、栈实现综合计算器
综合计算器的实现会用到逆/波兰表达式,只是功能更全面,支持"+"、"-"、"*"、"/"、"(" 、")",多位整数及小数运算。
代码示例:栈实现的综合计算器

1 public class MyCalculator { 2 3 public double calculate(String expression) { 4 // 1.中转后 5 final String suffixExpression = this.toSuffixExpression(expression); 6 7 System.out.println(suffixExpression); 8 9 // 2.计算后缀表达式 10 return Poland.calculateSuffix(suffixExpression); 11 } 12 13 /** 14 * 中缀表达式转后缀表达式.支持小数,多位整数 15 * 16 * @param infixExpression "12.8 + (2 - 3.55)*4+10/5.0" 17 * @return "12.8 2 3.55 - 4 * + 10 5.0 / +" 18 */ 19 private String toSuffixExpression(String infixExpression) { 20 if (infixExpression == null || "".equals((infixExpression = infixExpression.replaceAll("\\s+", "")))) { 21 throw new RuntimeException("infixExpression is illegal!"); 22 } 23 24 Stack<String> stack = new Stack<>(); 25 List<String> result = new ArrayList<>(); 26 27 StringBuilder builder = new StringBuilder(); 28 // 1.遍历 29 for (int i = 0; i < infixExpression.length(); i++) { 30 final char c = infixExpression.charAt(i); 31 32 // ①.数,就直接添加到result.注意:可能是多位数 或 小数 33 if (isDecimal(c)) { 34 builder.append(c); 35 36 // 可能会越界.有下一个且下一个是数 37 if (i != infixExpression.length() - 1 && isDecimal(infixExpression.charAt(i + 1))) { 38 continue; 39 } 40 41 result.add(builder.toString()); 42 43 // 清空 builder 44 builder.delete(0, builder.length()); 45 } else if (c == '(') { 46 stack.push(String.valueOf(c)); 47 } else if (c == ')') { 48 // stack依次出栈添加到result中直到遇到'(' 49 while (!"(".equals(stack.peek())) { 50 result.add(stack.pop()); 51 } 52 53 // 将'('弹出,消除这对括号 54 stack.pop(); 55 } else { 56 // ②.是运算符 57 while (!stack.empty() && !"(".equals(stack.peek()) && Poland.priority(String.valueOf(c), stack.peek()) <= 0) { 58 result.add(stack.pop()); 59 } 60 61 // 将c压栈 62 stack.push(String.valueOf(c)); 63 } 64 } 65 66 // 2.尾处理.将stack中剩余的运算符依次弹出加入result 67 while (!stack.empty()) { 68 result.add(stack.pop()); 69 } 70 71 // 3.此时result已是中缀表达式.用String输出 72 for (String s : result) { 73 builder.append(s) 74 .append(" "); 75 } 76 // 去除最后一个空格 77 if (builder.toString().length() != 0) { 78 builder.deleteCharAt(builder.length() - 1); 79 } 80 81 return builder.toString(); 82 } 83 84 /** 85 * 是不是小数 86 * 87 * @param val 88 * @return 89 */ 90 private boolean isDecimal(char val) { 91 // '0'[48] -> '9'[57] 92 return (val >= 48 && val <= 57) || val == '.'; 93 } 94 95 }
代码示例:测试类

1 // 测试类 2 public static void main(String[] args) { 3 MyCalculator calculator = new MyCalculator(); 4 final double v = calculator.calculate("12.8 + (2 - 3.55)*4+10/5.0"); 5 6 System.out.println("result = " + v); 7 } 8 9 // 结果 10 12.8 2 3.55 - 4 * + 10 5.0 / + 11 result = 8.600000000000001
作者:Craftsman-L
本博客所有文章仅用于学习、研究和交流目的,版权归作者所有,欢迎非商业性质转载。
如果本篇博客给您带来帮助,请作者喝杯咖啡吧!点击下面打赏,您的支持是我最大的动力!




 浙公网安备 33010602011771号
浙公网安备 33010602011771号