Note -「Suffix Automaton」SAM
Part. 1 基本信息
Part. 1-1 SAM 的构成。
SAM 由两个东西构成,一个是一个 DAWG,还有一棵外向树,叫 parent tree。
比如,给你一个字符串 \(S=\sf abbabb\),它的 SAM 长成这样:
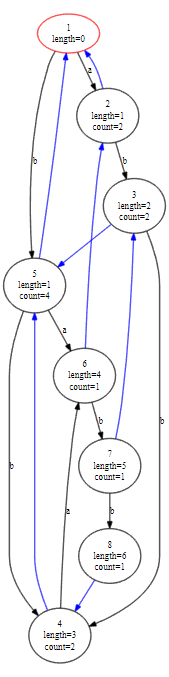
SAM 的 DAWG 大概可以理解为把字符串的所有后缀插入一个 Trie。当然如果你暴力插,点数为 \(\mathcal{O}(n^2)\)。
不过显然我们可以把一些重复的结点 rua 在一起,点数差不多就成了 \(\mathcal{O}(n)\),还要带个 \(2\) 的常数。
然后,\(S\) 的子串都可以被 SAM 的 DAWG 上的某条路径表示,很显,对吧。
DAWG 的边就是上图中的黑边,蓝边就是 parent tree 的树边。
Part. 1-2 符号约定
我们称 \(S[l,r]\) 为字符串 \(S\) 的 \([l,r]\) 的子串,相信大家都懂,下标从 \(1\) 开始。
我们称一个集合 \(\text{endpos}(S[l,r])\) 为:对于字符串 \(S\),\(S[l,r]\) 在 \(S\) 中出现的区间为 \([l_{1},r_{1}],\cdots,[l_{k},r_{k}]\),\(\text{endpos}(S[l,r])=\{r_{1},\cdots,r_{k}\}\)。
对于两个子串 \(x,y\),如果 \(\text{endpos}(x)=\text{endpos}(y)\),则称 \(x,y\) 在同一个 \(\text{endpos}\) 等价类中。
显然在 DAWG 上,从根节点到一个结点 \(u\) 能组成的字符串的长度是不同的(不同的路径组成的字符串长度不一定等),我们称从根节点到一个结点 \(u\) 能组成的最长的一个字符串的长度为 \(\text{maxlen}(u)\),最短的称为 \(\text{minlen}(u)\)。
Part. 2 需要知道的
Part. 2-1 \(\text{enspos}\) 的性质
引理 1:对于两个 \(S\) 的非空子串 \(x,y\)(不妨设 \(|x|<|y|\)),若 \(\text{endpos}(x)=\text{endpos}(y)\),则 \(x\) 为 \(y\) 的一个真后缀。
Obviously。
引理 2:对于两个 \(S\) 的非空子串 \(x,y\)(不妨设 \(|x|\le|y|\)),则
\[\begin{cases} \text{endpos}(x)\subseteq\text{endpos}(y),x\text{ is a suffix of } y, \\ \displaystyle\\ \text{endpos}(x)\cap\text{endpos}(y),\text{otherwise} \end{cases} \]
Obviously。
引理 3:在一个 \(\text{endpos}\) 等价类中,将类中的所有子串按长度非递增的顺序排序。每个子串都不会比它前一个子串长,与此同时每个子串也是它前一个子串的后缀。换句话说,对于同一等价类的任一两子串,较短者为较长者的后缀,且该等价类中的子串长度恰好覆盖整个区间 \([x,y]\)。
由引理 1,可知这些子串不会等长(对于两个串,较短串为较长串的真后缀),后面 obviously。
说得简单一点,把一个等价类里面最长的那个字符串拿出来,其他所有串都是该串的 suffix。
Part. 2-2 后缀链接 Link
后缀链接是在原串的 DAWG 上的点连出的边。后缀链接的链接遵循某种规则,且最后构成的是一棵树,我们把后缀链接连出来的树称为 Parent Tree,在后文我们将讲解这种规则。
我们先来看看一个串 \(S=\sf aababa\) 的 Parent Tree 长成副什么样子:

图是从 command_block 那里拿来的,可以沟通删除。(已经修正了原图的勘误)
为了说明方便,我们以一个任意的等价类来说明,我们称这个等价类中长度最大的串为 \(S_{\max}\),同理有 \(S_{\min}\)。
考虑在 \(S_{\max}\) 前面加上一个字符,称为新串为 \(S_{\text{new}}\),显然 \(S_{\text{new}}\) 一定不和 \(S_{\max}\) 在同一等价类里。
我们把上述 加字符 的操作看为分裂出儿子。有了这些,我们可以得出一些性质:
-
设 Parent Tree 上的父亲为 \(f\),儿子为 \(u\),有 \(\text{minlen}(u)=\text{maxlen}(f)+1\),显然。
-
点数边数皆为 \(\mathcal{O}(n)\),不考虑证明,背着。
-
在 Parent Tree 上,一个结点的父亲一定是该结点的后缀,显然。
最后板子自己理解性背住吧,构造方法不想写了。
struct SuffixAutomaton
{
int ID(char c)
{
return c-'a';
}
struct node
{
int len,link,ch[26];
}nodes[3000010];
int n,cntot,las,siz[3000010];
char s[1000010];
vector<int> e[3000010];
void init(int len,char c[])
{
n=len;
for(int i=1;i<=n;++i) s[i]=c[i];
nodes[0].len=las=cntot=0;
nodes[0].link=-1;
}
void extend(char c)
{
int cur=++cntot,one=las,ano=0;
nodes[cur].len=nodes[las].len+1;
while(~one&&!nodes[one].ch[ID(c)])
{
nodes[one].ch[ID(c)]=cur;
one=nodes[one].link;
}
if(one==-1) nodes[cur].link=0;
else
{
ano=nodes[one].ch[ID(c)];
if(nodes[one].len+1==nodes[ano].len) nodes[cur].link=ano;
else
{
int clone=++cntot;
nodes[clone].len=nodes[one].len+1;
nodes[clone].link=nodes[ano].link;
memcpy(nodes[clone].ch,nodes[ano].ch,sizeof(int)*26);
while(~one&&nodes[one].ch[ID(c)]==ano)
{
nodes[one].ch[ID(c)]=clone;
one=nodes[one].link;
}
nodes[ano].link=nodes[cur].link=clone;
}
}
siz[las=cur]=1;
}
void pre()
{
for(int i=1;i<=n;++i) extend(s[i]);
for(int i=1;i<=cntot;++i) e[nodes[i].link].push_back(i);
}
void dfs(int x)
{
for(int i=0;i<e[x].size();++i)
{
int y=e[x][i];
dfs(y);
siz[x]+=siz[y];
}
if(siz[x]^1) ans=max(ans,siz[x]*nodes[x].len);
}
}SAM;
代码中的 siz 是 \(\text{endpos}\) 集合大小。


