Ds100p -「数据结构百题」11~20
11.P3203 [HNOI2010]弹飞绵羊
某天,\(Lostmonkey\) 发明了一种超级弹力装置,为了在他的绵羊朋友面前显摆,他邀请小绵羊一起玩个游戏。
游戏一开始,\(Lostmonkey\) 在地上沿着一条直线摆上 \(n\) 个装置,每个装置设定初始弹力系数 \(k_i\),当绵羊达到第 \(i\) 个装置时,它会往后弹 \(k_i\) 步,达到第 \(i+k_i\) 个装置,若不存在第 \(i+k_i\) 个装置,则绵羊被弹飞。
绵羊想知道当它从第 \(i\) 个装置起步时,被弹几次后会被弹飞。为了使得游戏更有趣,\(Lostmonkey\) 可以修改某个弹力装置的弹力系数,任何时候弹力系数均为正整数。
每个弹力装置只会对应一个位置可以弹到,也就是说我们可以把它看作一条边,而且不会有环这种**玩意。
对于修改弹力系数,我们可以用断边连边来维护
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
const int SIZE = 2e5 + 5;
class LinkCutTree {
public:
struct SPLAY {
int val;
int fa;
int ch[2];
} T[SIZE];
inline bool isroot(int x) { return !(T[T[x].fa].ch[0] ^ x && T[T[x].fa].ch[1] ^ x); }
inline void push(int x) { T[x].val = T[T[x].ch[0]].val + T[T[x].ch[1]].val + 1; }
inline void rotate(int x) { int y = T[x].fa, z = T[y].fa, k = T[y].ch[1] == x, w = T[x].ch[!k]; (isroot(y)) && (T[z].ch[T[z].ch[1] == y] = x); T[x].ch[!k] = y, T[y].ch[k] = w; (w) && (T[w].fa = y); T[y].fa = x; T[x].fa = z; push(y); }
inline void splay(int x) { for(; isroot(x); rotate(x)) { int y = T[x].fa, z = T[y].fa; (isroot(y)) && (rotate(T[y].ch[1] ^ x ^ T[z].ch[1] ^ y ? x : y), 1); } push(x); }
inline void access(int x) { for(int y = 0; x; x = T[y = x].fa) splay(x), T[x].ch[1] = y, push(x); }
} lct_mast;
int n, m;
signed main() {
scanf("%d", &n);
for(int i = 1, s; i <= n; ++i) {
lct_mast.T[i].val = 1;
scanf("%d", &s);
(i + s <= n) && (lct_mast.T[i].fa = i + s);
}
for(scanf("%d", &m); m; --m) {
int opt, x, y;
scanf("%d", &opt), scanf("%d", &x);
if (opt ^ 2) {
lct_mast.access(x + 1);
lct_mast.splay(x + 1);
printf("%d\n", lct_mast.T[x + 1].val);
} else {
scanf("%d", &y);
lct_mast.access(x + 1);
lct_mast.splay(x + 1);
lct_mast.T[x + 1].ch[0] = lct_mast.T[lct_mast.T[x + 1].ch[0]].fa = 0;
(x + y + 1 <= n) && (lct_mast.T[x + 1].fa = x + y + 1);
lct_mast.push(x + 1);
}
}
return 0;
}
12.SP4487 GSS6 - Can you answer these queries VI
The first line of the input contains an integer N.
The following line contains N integers, representing the starting
sequence A1..AN, (|Ai| <= 10000).
The third line contains an integer Q. The next Q lines contains the operations in following form:
I x y: insert element y at position x (between x - 1 and x).
D x : delete the element at position x.
R x y: replace element at position x with y.
Q x y: print max{Ai + Ai+1 + .. + Aj | x <= i <= j <= y}.
All given positions are valid, and given values are between -10000 and +10000.
The sequence will never be empty.
这道题显然是一道平衡树的裸题,唯一的难度就是求最大子段和。
可以类比线段树维护最大子段和,维护\(lmax\)以x为根的前缀最大和、\(rmax\)以x为根的后缀最大和、\(maxsum\)最大子段和以及\(sum\)总和
对于\(Update\)我们可以对是否有左右孩子做讨论。
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <queue>
#include <utility>
using namespace std;
const int SIZE = 2e5 + 5;
int n, m, tot, root, a[SIZE];
struct SPLAY {
int fa;
int ch[2];
int siz;
int val;
int sum;
int lmax;
int rmax;
int maxsum;
} T[SIZE];
vector < int > st;
inline int newnode(int v = 0) {
int x;
if (st.empty()) x = ++tot;
else x = st.back(), st.pop_back();
T[x].fa = T[x].ch[0] = T[x].ch[1] = 0;
T[x].siz = 1;
T[x].val = T[x].sum = T[x].maxsum = v;
T[x].lmax = T[x].rmax = max(v, 0);
return x;
}
inline void delnode(int x) {
T[x].fa = T[x].ch[0] = T[x].ch[1] = 0;
T[x].sum = T[x].lmax = T[x].rmax = T[x].maxsum = 0;
T[x].siz = 1;
st.push_back(x);
}
inline bool which(int x) {
if (T[T[x].fa].ch[0] == x) return 0;
if (T[T[x].fa].ch[1] == x) return 1;
return -1;
}
inline void update(int x) {
T[x].sum = T[x].val; T[x].siz = 1;
if (T[x].ch[0]) T[x].sum += T[T[x].ch[0]].sum, T[x].siz += T[T[x].ch[0]].siz;
if (T[x].ch[1]) T[x].sum += T[T[x].ch[1]].sum, T[x].siz += T[T[x].ch[1]].siz;
if (T[x].ch[0] && T[x].ch[1]) {
T[x].lmax = max(T[T[x].ch[0]].lmax, T[T[x].ch[0]].sum + T[x].val + T[T[x].ch[1]].lmax);
T[x].rmax = max(T[T[x].ch[1]].rmax, T[T[x].ch[1]].sum + T[x].val + T[T[x].ch[0]].rmax);
T[x].maxsum = max({T[T[x].ch[0]].maxsum, T[T[x].ch[1]].maxsum, T[T[x].ch[0]].rmax + T[x].val + T[T[x].ch[1]].lmax});
} else if (T[x].ch[0]) {
T[x].lmax = max({T[T[x].ch[0]].lmax, T[T[x].ch[0]].sum + T[x].val, 0});
T[x].rmax = max(T[x].val + T[T[x].ch[0]].rmax, 0);
T[x].maxsum = max(T[T[x].ch[0]].maxsum, T[T[x].ch[0]].rmax + T[x].val);
} else if (T[x].ch[1]) {
T[x].lmax = max(T[x].val + T[T[x].ch[1]].lmax, 0);
T[x].rmax = max({T[T[x].ch[1]].rmax, T[T[x].ch[1]].sum + T[x].val, 0});
T[x].maxsum = max(T[T[x].ch[1]].maxsum, T[T[x].ch[1]].lmax + T[x].val);
} else {
T[x].maxsum = T[x].val;
T[x].lmax = T[x].rmax = max(T[x].val, 0);
}
}
inline void rotate(int x) {
if (!x) return;
int w = which(x), y = T[x].fa;
if (~which(y)) T[T[y].fa].ch[which(y)] = x;
T[x].fa = T[y].fa;
T[y].ch[w] = T[x].ch[w ^ 1];
if (T[x].ch[w ^ 1]) T[T[x].ch[w ^ 1]].fa = y;
T[x].ch[w ^ 1] = y;
T[y].fa = x;
update(y), update(x);
}
inline void splay(int x, int &goal) {
if (x == goal) return;
int p = T[goal].fa;
for (int y; T[x].fa ^ p; rotate(x)) y = T[x].fa, (T[y].fa ^ p) && (rotate(which(y) ^ which(x) ? x : y), 1);
goal = x;
}
inline int kth_element(int x, int k) {
while (233) {
if (T[x].ch[0] && k <= T[T[x].ch[0]].siz) x = T[x].ch[0];
else {
if (T[x].ch[0]) k -= T[T[x].ch[0]].siz;
if (!--k) return x;
x = T[x].ch[1];
}
}
}
inline void insert(int &rt, int p, int val) {
int x = kth_element(rt, p);
splay(x, rt);
int y = kth_element(rt, p + 1);
splay(y, T[rt].ch[1]);
T[y].ch[0] = newnode(val);
T[T[y].ch[0]].fa = y;
update(T[y].ch[0]);
update(y), update(x);
}
inline void erase(int &rt, int p) {
int y = kth_element(rt, p);
splay(y, rt);
int x = kth_element(rt, p + 1);
splay(x, T[rt].ch[1]);
int z = T[x].ch[1];
T[z].fa = y;
T[y].ch[1] = z;
delnode(x);
update(y);
}
inline void modify(int &rt, int p, int val) {
int x = kth_element(rt, p + 1);
splay(x, rt);
T[x].val = val;
update(x);
}
inline int find(int &rt, int l, int r) {
int x = kth_element(rt, l);
splay(x, rt);
int y = kth_element(rt, r + 2);
splay(y, T[rt].ch[1]);
return T[T[y].ch[0]].maxsum;
}
inline void make(int p, int l, int r) {
int mid = (l + r) >> 1;
T[p].val = a[mid];
if (mid - 1 >= l) T[p].ch[0] = newnode(), T[T[p].ch[0]].fa = p, make(T[p].ch[0], l, mid - 1);
if (mid + 1 <= r) T[p].ch[1] = newnode(), T[T[p].ch[1]].fa = p, make(T[p].ch[1], mid + 1, r);
update(p);
}
signed main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]);
int root = newnode();
make(root, 0, n + 1);
scanf("%d", &m);
for (int i = 1; i <= m; ++i) {
char opt[2];
int x, y;
scanf("%s %d", opt, &x);
if (*opt ^ 'D') scanf("%d", &y);
if (*opt == 'I') insert(root, x, y);
if (*opt == 'D') erase(root, x);
if (*opt == 'R') modify(root, x, y);
if (*opt == 'Q') printf("%d\n", find(root, x, y));
}
return 0;
}
13.Count on a tree
给定一棵 \(n\) 个节点的树,每个点有一个权值。有 \(m\) 个询问,每次给你 \(u\),\(v\),\(k\) 你需要回答 \(u \text{ xor last}\) 和 \(v\) 这两个节点间第 \(k\) 小的点权。
LYC
树上的路径问题,我们一般都要用树链剖分。
静态第\(k\)小的问题,我们一般用主席树。
经过严谨分析,我们得出,这道题是树剖加主席树。
把树剖成重链之后像主席树模板那样按\(dfs\)序插入每个数(让同一条重链在主席树的\(root\)数组中成为一个连续的区间,方便统计),然后我们要查询\(u\),\(v\)两个节点间的第\(k\)小。
和模板不一样的地方来了:这里的区间第\(k\)小的区间不连续。
我们回想模板的思想过程:
通过差分得出区间内每个数值出现的个数。
既然这次区间是不连续的,我们就每次都把这些不连续的子区间统计一遍,再加起来就好了,就相当于是把这些子区间合起来。
具体来说,就是树剖\(LCA\)时记录每个区间的左右端点。使用主席树查询时再把原来的对于一个区间的统计改为对很多区间的统计就好了。
剩下的就和模板一样了。
代码:
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
int n,m,p,a[100010],last,u,v,w,fa[100010],dep[100010],son[100010],siz[100010],dfn[100010],ton[100010],hb[100010],tot,be[100010],en[100010],cnt,root[100010],cntot;
struct node
{
int l,r,sum;
}nodes[4000010];
vector<int> e[100010],pri;
int getID(int val)
{
return lower_bound(pri.begin(),pri.end(),val)-pri.begin()+1;
}//离散化
void dfs1(int x,int las)
{
dep[x]=dep[las]+1;
fa[x]=las;
siz[x]=1;
int b=-1e9,s=0;
for(int i=0;i<e[x].size();++i)
{
int y=e[x][i];
if(y^las)
{
dfs1(y,x);
siz[x]+=siz[y];
if(siz[y]>b)
{
b=siz[y];
s=y;
}
}
}
son[x]=s;
}
void dfs2(int x,int las,int heavy)
{
if(heavy) hb[x]=hb[las];
else hb[x]=x;
dfn[x]=++tot;
ton[tot]=a[x];
if(son[x]) dfs2(son[x],x,1);
for(int i=0;i<e[x].size();++i)
{
int y=e[x][i];
if(y^las&&y^son[x]) dfs2(y,x,0);
}
}
void LCA(int x,int y)
{
int fx=hb[x],fy=hb[y];
while(fx^fy)
{
if(dep[fx]<dep[fy])
{
swap(fx,fy);
swap(x,y);
}
be[++cnt]=root[dfn[fx]-1];
en[cnt]=root[dfn[x]];//记录每一个区间的左端点-1和右端点,相当于原来find(int l,int r,int p1,int p2,int k)中的p1,p2。
x=fa[fx];
fx=hb[x];
}
be[++cnt]=root[min(dfn[x],dfn[y])-1];
en[cnt]=root[max(dfn[x],dfn[y])];
//所有的子区间中的数包含且仅包含了u到v的最短路径上的所有点。因为树剖LCA会用一个一个区间覆盖所有点,而我们记录了每一个区间。
}//树剖
void ins(int l,int r,int pre,int &now,int pos)
{
nodes[++cntot]=nodes[pre];
now=cntot;
++nodes[now].sum;
if(l==r) return;
int mid=(l+r)>>1;
if(pos<=mid) ins(l,mid,nodes[pre].l,nodes[now].l,pos);
else ins(mid+1,r,nodes[pre].r,nodes[now].r,pos);
}
int find(int l,int r,int k)
{
if(l==r) return pri[l-1];//一直到确定第k小的位置;返回原值。
int X=0;
for(int i=1;i<=cnt;++i) X+=(nodes[nodes[en[i]].l].sum-nodes[nodes[be[i]].l].sum);
//临时统计u到v的最短路径上的所有点权中在[l,mid]中的数的个数。
int mid=(l+r)>>1;
if(k<=X)//k<=X,说明第k小在左边
{
for(int i=1;i<=cnt;++i)//把每个端点都往左下跳。使它代表的值为这个区间的元素值在[l,mid]的个数。
{
en[i]=nodes[en[i]].l;
be[i]=nodes[be[i]].l;
}
//然后我们就可以去缩小范围,去查询[l,mid]这个区间了。
return find(l,mid,k);
}
else//否则,第k小是右边的第k-X小
{
for(int i=1;i<=cnt;++i)//把每个端点都往右下跳。道理同上。
{
en[i]=nodes[en[i]].r;
be[i]=nodes[be[i]].r;
}
return find(mid+1,r,k-X);//继续查找
}
}//主席树
int main()
{
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
pri.push_back(a[i]);
}
for(int i=1;i<n;++i)
{
scanf("%d %d",&u,&v);
e[u].push_back(v);
e[v].push_back(u);
}
sort(pri.begin(),pri.end());
pri.erase(unique(pri.begin(),pri.end()),pri.end());
dfs1(1,1);
dfs2(1,1,0);
p=pri.size();
for(int i=1;i<=n;++i) ins(1,p,root[i-1],root[i],getID(ton[i]));//按dfs序插入
for(int i=1;i<=m;++i)
{
scanf("%d %d %d",&u,&v,&w);
u^=last;
cnt=0;
LCA(u,v);
last=find(1,p,w);
printf("%d\n",last);
}
return 0;
}
WGY
对于每一个节点\(x\),先令\(rt_x=rt_{x-1}\),然后在\(rt_x\)中插入\(a_i\),这样其实每个节点维护的都是节点到根的信息
对于查询操作中的每一个\((x,y)\),我们可以用\(rt_x+rt_y-rt_{lca_{x,y}}-rt_{fa_{lca_{x,y}}}\)来得到答案
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#define mid ((l + r) >> 1)
const int SIZE = 1e5 + 5;
struct TreeNode {
int l, r;
int size;
} fhq[SIZE << 5];
int n, m, tot, fa[SIZE], rt[SIZE];
int a[SIZE], rnk[SIZE], dp[SIZE], inq[30][SIZE], lastans, Q[SIZE];
std::vector < std::vector < int > > G(SIZE);
inline bool cmp(int x, int y) { return a[x] < a[y]; }
inline void newnode(int t, int p) {
fhq[++tot] = fhq[rt[t]];
rt[t] = tot;
int u = rt[t], l = 1, r = n;
while (l ^ r) {
fhq[u].size++;
if (p <= mid) fhq[++tot] = fhq[fhq[u].l], fhq[u].l = tot, u = fhq[u].l, r = mid;
else fhq[++tot] = fhq[fhq[u].r], fhq[u].r = tot, u = fhq[u].r, l = mid + 1;
}
fhq[u].size++;
}
inline int find(int a, int b, int c, int d, int l, int r, int u) {
if (l ^ r)
if (fhq[fhq[a].l].size + fhq[fhq[b].l].size - fhq[fhq[c].l].size - fhq[fhq[d].l].size >= u) return find(fhq[a].l, fhq[b].l, fhq[c].l, fhq[d].l, l, mid, u);
else return find(fhq[a].r, fhq[b].r, fhq[c].r, fhq[d].r, mid + 1, r, u - (fhq[fhq[a].l].size + fhq[fhq[b].l].size - fhq[fhq[c].l].size - fhq[fhq[d].l].size));
else return l;
}
inline void dfs(int x, int fa) {
dp[x] = dp[fa] + 1;
rt[x] = rt[fa];
::fa[x] = fa;
newnode(x, a[x]);
for (int i = 0; i < (int)G[x].size(); ++i) if (G[x][i] ^ fa) dfs(G[x][i], x);
}
inline int lca_mast(int x, int y) {
if (dp[x] < dp[y]) std::swap(x, y);
for (int i = 0; dp[x] - dp[y]; ++i) if ((1 << i) & (dp[x] - dp[y])) x = inq[i][x];
if (x ^ y) { for (int i = 25; i >= 0; --i) if (inq[i][x] ^ inq[i][y]) x = inq[i][x], y = inq[i][y]; return fa[x]; }
else return x;
}
signed main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i]), Q[i] = i;
std::sort(Q + 1, Q + 1 + n, cmp);
for (int i = 1; i <= n; ++i) rnk[i] = a[Q[i]], a[Q[i]] = i;
for (int i = 1, x, y; i < n; ++i) scanf("%d %d", &x, &y), G[x].push_back(y), G[y].push_back(x);
dfs(1, 0);
for (int i = 1; i <= n; ++i) inq[0][i] = fa[i];
for (int i = 1; i < 26; ++i) for (int j = 1; j <= n; ++j) inq[i][j] = inq[i - 1][inq[i - 1][j]];
for (int i = 1; i <= m; ++i) {
int x, y, z;
scanf("%d %d %d", &x, &y, &z);
x ^= lastans;
int lca = lca_mast(x, y);
printf("%d\n", lastans = rnk[find(rt[x], rt[y], rt[lca], rt[fa[lca]], 1, n, z)]);
}
return 0;
}
14.P2486 [SDOI2011]染色

WGY
可以把首先把连接不同色点的边权设置为1,同色的设为9,这样整个问题就变成了查询路径上的权值和。
显然,我们可以用暴力\(LinkCutTree\)或\(TreeChainSplitting\)来搞,这里给出\(LCT\)的做法。
维护每一个\(Splay\)节点的最左端点的值和最右端点的颜色,对于它的老汉节点,我们可以找出它的前驱和后继的颜色。这样就可以累计它和前驱和后继连边的权值和辣
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#define lson (fhq[x].ch[0])
#define rson (fhq[x].ch[1])
using namespace std;
#define DEBUG 1 // debug toggle
struct IO {
#define MAXSIZE (1 << 20)
#define isdigit(x) (x >= '0' && x <= '9')
char buf[MAXSIZE], *p1, *p2;
char pbuf[MAXSIZE], *pp;
#if DEBUG
#else
IO() : p1(buf), p2(buf), pp(pbuf) {}
~IO() { fwrite(pbuf, 1, pp - pbuf, stdout); }
#endif
inline char gc() {
#if DEBUG
return getchar();
#endif
if (p1 == p2) p2 = (p1 = buf) + fread(buf, 1, MAXSIZE, stdin);
return p1 == p2 ? ' ' : *p1++;
}
inline bool blank(char ch) {
return ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t';
}
template <class T>
inline void read(T &x) {
register double tmp = 1;
register bool sign = 0;
x = 0;
register char ch = gc();
for (; !isdigit(ch); ch = gc())
if (ch == '-') sign = 1;
for (; isdigit(ch); ch = gc()) x = x * 10 + (ch - '0');
if (ch == '.')
for (ch = gc(); isdigit(ch); ch = gc())
tmp /= 10.0, x += tmp * (ch - '0');
if (sign) x = -x;
}
inline void read(char *s) {
register char ch = gc();
for (; blank(ch); ch = gc())
;
for (; !blank(ch); ch = gc()) *s++ = ch;
*s = 0;
}
inline void read(char &c) {
for (c = gc(); blank(c); c = gc())
;
}
inline void push(const char &c) {
#if DEBUG
putchar(c);
#else
if (pp - pbuf == MAXSIZE) fwrite(pbuf, 1, MAXSIZE, stdout), pp = pbuf;
*pp++ = c;
#endif
}
template <class T>
inline void write(T x) {
if (x < 0) x = -x, push('-');
static T sta[35];
T top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
while (top) push(sta[--top] + '0');
}
template <class T>
inline void write(T x, char lastChar) {
write(x), push(lastChar);
}
} io;
const int SIZE = 1e6 + 5;
int n, m;
class LinkCutTree {
public:
struct SPLAY {
int w, c;
int l, r;
int tag, rev;
int fa, ch[2];
} fhq[SIZE]; // The fhq-treap replaces the splay
// Struct SPLAY
int stack[SIZE], tp;
inline bool isroot(int x) { return fhq[fhq[x].fa].ch[0] ^ x && fhq[fhq[x].fa].ch[1] ^ x; }
inline void tr_dn1(int x) { if (fhq[x].rev) swap(lson, rson), swap(fhq[lson].l, fhq[lson].r), swap(fhq[rson].l, fhq[rson].r), fhq[lson].rev ^= 1, fhq[rson].rev ^= 1, fhq[x].rev = 0; }
inline void tr_dn2(int x) { if (fhq[x].tag) fhq[x].l = fhq[x].r = fhq[x].c = fhq[x].tag, fhq[lson].tag = fhq[rson].tag = fhq[x].tag, fhq[x].w = fhq[x].tag = 0; }
inline void tr_dn(int x) { tr_dn1(x), tr_dn2(x); }
inline void tr_up_(int x) { tr_dn(lson), tr_dn(rson); fhq[x].w = fhq[lson].w + fhq[rson].w; }
inline void tr_up1(int x) { if (lson) fhq[x].l = fhq[lson].l, ((fhq[x].c ^ fhq[lson].r) && (++fhq[x].w, 1)); else fhq[x].l = fhq[x].c; }
inline void tr_up2(int x) { if (rson) fhq[x].r = fhq[rson].r, ((fhq[x].c ^ fhq[rson].l) && (++fhq[x].w, 1)); else fhq[x].r = fhq[x].c; }
inline void tr_up(int x) { tr_up_(x); tr_up1(x); tr_up2(x); }
inline void rotate(int x) { int y = fhq[x].fa, z = fhq[y].fa, k = fhq[y].ch[1] == x; if (!isroot(y)) fhq[z].ch[fhq[z].ch[1] == y] = x; fhq[x].fa = z; fhq[y].ch[k] = fhq[x].ch[k ^ 1], fhq[fhq[x].ch[k ^ 1]].fa = y; fhq[x].ch[k ^ 1] = y; fhq[y].fa = x; tr_up(y); }
inline void splay1(int x) { stack[tp = 1] = x; for (int i = x; !isroot(i); i = fhq[i].fa) stack[++tp] = fhq[i].fa; while (tp) tr_dn(stack[tp--]); }
inline void splay2(int x) { for (; !isroot(x); rotate(x)) { int y = fhq[x].fa, z = fhq[y].fa; if (!isroot(y)) (fhq[y].ch[1] ^ x ^ fhq[z].ch[1] ^ y) ? rotate(x) : rotate(y); } }
inline void splay(int x) { splay1(x), splay2(x); tr_up(x); }
inline void access(int x) { for (int y = 0; x; y = x, x = fhq[x].fa) splay(x), rson = y, tr_up(x); }
inline void makeroot(int x) { access(x), splay(x), fhq[x].rev ^= 1; }
inline int findroot(int x) { access(x), splay(x); while (lson) x = lson; return x; }
inline void split(int x, int y) { makeroot(x), access(y), splay(y); }
inline void connect(int x, int y) { makeroot(x), fhq[x].fa = y; }
} lct_mast; // Class LinkCutTree
signed main() {
io.read(n), io.read(m);
for (int i = 1, x; i <= n; ++i) io.read(x), lct_mast.fhq[i].c = lct_mast.fhq[i].l = lct_mast.fhq[i].r = x;
for (int i = 1, x, y; i < n; ++i) io.read(x), io.read(y), lct_mast.connect(x, y);
for (int i = 1, a, b, c; i <= m; ++i) {
char ch = getchar();
while (ch ^ 'C' && ch ^ 'Q') ch = getchar();
if (ch ^ 'Q') io.read(a), io.read(b), io.read(c), lct_mast.split(a, b), lct_mast.fhq[b].tag = c;
else io.read(a), io.read(b), lct_mast.split(a, b), io.write(lct_mast.fhq[b].w + 1, '\n');
}
return 0;
}
LYC
15.「ZJOI2017」树状数组
漆黑的晚上,九条可怜躺在床上辗转反侧。难以入眠的她想起了若干年前她的一次悲惨的OI比赛经历。那是一道基础的树状数组题。
给出一个长度为\(n\)的数组\(A\),初始值都为0,接下来进行\(m\)次操作,操作有两种:
* 1 x,表示将 \(A_{x}\) 变成 \(\left ( A_{x}+ 1 \right )\) mod 2。
* 2 l r,表示询问 $ \left ( \sum_{i=l}^{r} A_{i} \right )$ mod 2。
尽管那个时候的可怜非常的 simple,但是她还是发现这题可以用树状数组做。当时非常young 的她写了如下的算法:

其中 lowbit(\(x\)) 表示数字 \(x\) 最低的非 0 二进制位,例如 lowbit(5) = 1, lowbit(12) = 4。进行第一类操作的时候就调用 Add(\(x\)),第二类操作的时候答案就是 Query(\(l\),\(r\))。
如果你对树状数组比较熟悉,不难发现可怜把树状数组写错了: Add 和 Find 中 \(x\) 变化的方向反了。因此这个程序在最终测试时华丽的爆 0 了。
然而奇怪的是,在当时,这个程序通过了出题人给出的大样例——这也是可怜没有进行对
拍的原因。
现在,可怜想要算一下,这个程序回答对每一个询问的概率是多少,这样她就可以再次的
感受到自己是一个多么非的人了。然而时间已经过去了很多年,即使是可怜也没有办法完全回忆起当时的大样例。幸运的是,她回忆起了大部分内容,唯一遗忘的是每一次第一类操作的 \(x\)
的值,因此她假定这次操作的 \(x\) 是在 \(\left [ l_{i},r_{i} \right ]\) 范围内 等概率随机 的。
具体来说,可怜给出了一个长度为 \(n\) 的数组 \(A\),初始为 0,接下来进行了 \(m\) 次操作:
* 1 \(l\) \(r\),表示在区间 \(\left [ l, r \right ]\) 中等概率选取一个 \(x\) 并执行 Add(\(x\))。
* 2 \(l\) \(r\),表示询问执行 Query\(\left ( l, r \right )\)得到的结果是正确的概率是多少。
这道题\(\cdots\),没什么可讲的吧?二维线段树蛮干就好了
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#define mid ((l + r) >> 1)
using namespace std;
typedef long long int ull;
const int SIZE = 1e5 + 5;
const int MOD = 998244353;
struct TreeNode {
int l, r;
int val;
} tr[SIZE * 400];
int rt[SIZE * 20], n, q, tot;
inline ull result(ull p, ull q) {
ull res = p * q; res %= MOD;
return res = (res + (1 - p + MOD) * (1 - q + MOD) % MOD) % MOD;
}
inline ull fast_pow(ull x, ull y) {
ull res = 1;
for (; y; y >>= 1, (x *= x) %= MOD) if (y & 1) (res *= x) %= MOD;
return res % MOD;
}
inline void modifies(int l, int r, int &rt, int x, int y, ull p) {
if (!rt) rt = ++tot, tr[rt].val = 1;
if (l >= x && r <= y) return (void)(tr[rt].val = result(p, tr[rt].val));
if (mid >= x) modifies(l, mid, tr[rt].l, x, y, p);
if (mid < y) modifies(mid + 1, r, tr[rt].r, x, y, p);
}
inline void modify(int l, int r, int rt, int lx, int rx, int ly, int ry, ull p) {
if (l >= lx && r <= rx) return (void)(modifies(1, n, ::rt[rt], ly, ry, p));
if (mid >= lx) modify(l, mid, rt << 1, lx, rx, ly, ry, p);
if (mid < rx) modify(mid + 1, r, rt << 1 | 1, lx, rx, ly, ry, p);
}
inline ull finds(int l, int r, int rt, int x) {
if (!rt) return 1;
if (l ^ r)
if (mid >= x) return result(tr[rt].val, finds(l, mid, tr[rt].l, x));
else return result(tr[rt].val, finds(mid + 1, r, tr[rt].r, x));
else return tr[rt].val;
}
inline ull find(int l, int r, int rt, int x, int y) {
if (l ^ r)
if (mid >= x) return result(finds(1, n, ::rt[rt], y), find(l, mid, rt << 1, x, y));
else return result(finds(1, n, ::rt[rt], y), find(mid + 1, r, rt << 1 | 1, x, y));
else return finds(1, n, ::rt[rt], y);
}
signed main() {
scanf("%d %d", &n, &q);
for (int i = 0; i < q; ++i) {
int opt, l, r;
scanf("%d %d %d", &opt, &l, &r);
if (opt ^ 1) printf("%lld\n", find(0, n, 1, l - 1, r));
else {
ull p = fast_pow(r - l + 1, MOD - 2);
if (l > 1) modify(0, n, 1, 1, l - 1, l, r, (1 - p + MOD) % MOD), modify(0, n, 1, 0, 0, 1, l - 1, 0);
if (r < n) modify(0, n, 1, l, r, r + 1, n, (1 - p + MOD) % MOD), modify(0, n, 1, 0, 0, r + 1, n, 0);
modify(0, n, 1, l, r, l, r, (1 - p * 2 % MOD + MOD) % MOD), modify(0, n, 1, 0, 0, l, r, p);
}
}
return 0;
}
16.P2161 [SHOI2009]会场预约
// 未免LJS吐槽不贴题面了
这道题正解应该是平衡树或者BIT,这里提供一种简便的STL做法。
对于第一个操作,我们可以令有冲突的预约相等,避免set特性坑死一票人
对于第二个操作直接输出set的大小即可
// 省略头文件和快读
struct LaLaLand {
int l, r;
bool operator < (const LaLaLand& rhs) const { return r < rhs.l; }
};
set < LaLaLand > st;
int T;
signed main() {
for (read(T); T; --T) {
char opt[5];
read(opt);
int l, r, cnt = 0;
if (*opt == 'A') {
read(l, r);
LaLaLand tmp = {l, r};
IT it = st.find(tmp);
while (it != st.end()) ++cnt, st.erase(it), it = st.find(tmp);
st.insert(tmp);
write(io_l, cnt);
}
else write(io_l, st.size());
}
return 0;
}
17.SP11470 TTM - To the moon
一个长度为n的数组,4种操作 :
-
C l r d:区间 \([l,r]\) 中的数都加 \(d\) ,同时当前的时间戳加 \(1\)。 -
Q l r:查询当前时间戳区间 \([l,r]\) 中所有数的和 。 -
H l r t:查询时间戳 \(t\) 区间 \([l,r]\) 的和 。 -
B t:将当前时间戳置为 \(t\) 。
这道题正解应该是主席树+标记永久化,我来提供一种代码极短(压行后不到1K)的做法(怎么感觉我就没什么正经解法)
维护一个差分数组,将每次询问看作是两次前缀和相减
然后...就没有然后了,其它都是模板的主席树,只是修改用差分就好了
18.P4168 [Violet]蒲公英
在乡下的小路旁种着许多蒲公英,而我们的问题正是与这些蒲公英有关。
为了简化起见,我们把所有的蒲公英看成一个长度为n的序列 \((a_1,a_2..a_n)\),其中 \(a_i\) 为一个正整数,表示第i棵蒲公英的种类编号。
而每次询问一个区间 [l,r],你需要回答区间里出现次数最多的是哪种蒲公英,如果有若干种蒲公英出现次数相同,则输出种类编号最小的那个。
注意,你的算法必须是在线的
LYC:
这就是传说中的分块打表了
由于强制在线,莫队是不可能的了
求区间众数,我们可以按之前讲的分块打表技术,处理出每两个特征点的每个元素的出现个数和当前众数。
对于每个询问,由于众数问题不容易往回收(要重新找众数),我们选取左右端点往内的最近的特征点
继承(注意不是直接把这个区间的答案拿来接着用,因为不能回退,如果直接用又不回退,下次调用时会调到错误的结果)这个区间的答案,利用这个区间之前统计的元素出现个数
向外扩张,统计出要询问的答案
最后要把刚刚统计众数加上的元素个数清掉(回溯最初处理好的状态)
代码:(这里块大小我开的\(n^{2/3}\),开\(\sqrt n\)好像开不下)
#include<cmath>
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
vector<int> pri;
int n,m,a[40010],each,cnt[40][40][40010],MAX[40][40],lans,l,r,ans,tmp[40010];
int main()
{
scanf("%d %d",&n,&m);
each=pow(n,2.0/3);
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]);
pri.push_back(a[i]);
}
sort(pri.begin(),pri.end());
pri.erase(unique(pri.begin(),pri.end()),pri.end());
for(int i=1;i<=n;++i) a[i]=lower_bound(pri.begin(),pri.end(),a[i])-pri.begin()+1;//离散化
for(int i=1,p=1;i<=n;i+=each,++p)
{
for(int j=i+each-1,q=p;j<=n;j+=each,++q)
{
for(int k=i;k<=j;++k)
{
++cnt[p][q][a[k]];
if(cnt[p][q][a[k]]>cnt[p][q][MAX[p][q]]||(cnt[p][q][a[k]]==cnt[p][q][MAX[p][q]]&&a[k]<MAX[p][q])) MAX[p][q]=a[k];
}
}
}//初始化(打表)
for(int i=1;i<=m;++i)
{
scanf("%d %d",&l,&r);
l=(l+lans-1)%n+1;
r=(r+lans-1)%n+1;
if(l>r) swap(l,r);//强制在线
if(r-l>2*each)
{
int p=ceil(1.0*(l-1)/each)+1;
int q=ceil(1.0*(r+1)/each)-1;//得到向内收缩的端点
ans=MAX[p][q];//继承答案
for(int i=(p-1)*each;i>=l;--i)
{
++cnt[p][q][a[i]];
if(cnt[p][q][a[i]]>cnt[p][q][ans]||(cnt[p][q][a[i]]==cnt[p][q][ans]&&a[i]<ans)) ans=a[i];
}
for(int i=q*each+1;i<=r;++i)
{
++cnt[p][q][a[i]];
if(cnt[p][q][a[i]]>cnt[p][q][ans]||(cnt[p][q][a[i]]==cnt[p][q][ans]&&a[i]<ans)) ans=a[i];
}
lans=pri[ans-1];//获得原值
printf("%d\n",lans);
for(int i=(p-1)*each;i>=l;--i) --cnt[p][q][a[i]];
for(int i=q*each+1;i<=r;++i) --cnt[p][q][a[i]];//回溯
}
else//区间太小,如果两个端点在一个块内,向内收缩就会重复统计整个块,所以暴力统计
{
ans=0;
for(int i=l;i<=r;++i)
{
++tmp[a[i]];
if(tmp[a[i]]>tmp[ans]||(tmp[a[i]]==tmp[ans]&&a[i]<ans)) ans=a[i];
}
lans=pri[ans-1];
printf("%d\n",lans);
for(int i=l;i<=r;++i) --tmp[a[i]];//回溯清零
}
}
return 0;
}
WGY:
这道题luogu的数据很水,于是...于是...我们直接离散化+暴力就能过!
然后....然后就没了(这次真的不是我不想写,是真的没什么写的...)
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#define mid ((l + r) >> 1)
#define mp make_pair
#define fir first
#define sec second
#define pub push_back
#define pob pop_back
using namespace std;
typedef long long LL;
// #define DEBUG 1
struct IO {
#define MAXSIZE (1 << 20)
#define isdigit(x) (x >= '0' && x <= '9')
char buf[MAXSIZE], *p1, *p2;
char pbuf[MAXSIZE], *pp;
#if DEBUG
#else
IO() : p1(buf), p2(buf), pp(pbuf) {}
~IO() { fwrite(pbuf, 1, pp - pbuf, stdout); }
#endif
inline char gc() {
#if DEBUG
return getchar();
#endif
if (p1 == p2) p2 = (p1 = buf) + fread(buf, 1, MAXSIZE, stdin);
return p1 == p2 ? ' ' : *p1++;
}
inline bool blank(char ch) {
return ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t';
}
template <class T>
inline void read(T &x) {
register double tmp = 1;
register bool sign = 0;
x = 0;
register char ch = gc();
for (; !isdigit(ch); ch = gc())
if (ch == '-') sign = 1;
for (; isdigit(ch); ch = gc()) x = x * 10 + (ch - '0');
if (ch == '.')
for (ch = gc(); isdigit(ch); ch = gc())
tmp /= 10.0, x += tmp * (ch - '0');
if (sign) x = -x;
}
inline void read(char *s) {
register char ch = gc();
for (; blank(ch); ch = gc())
;
for (; !blank(ch); ch = gc()) *s++ = ch;
*s = 0;
}
inline void read(char &c) {
for (c = gc(); blank(c); c = gc())
;
}
inline void push(const char &c) {
#if DEBUG
putchar(c);
#else
if (pp - pbuf == MAXSIZE) fwrite(pbuf, 1, MAXSIZE, stdout), pp = pbuf;
*pp++ = c;
#endif
}
template <class T>
inline void write(T x) {
if (x < 0) x = -x, push('-');
static T sta[35];
T top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
while (top) push(sta[--top] + '0');
}
template <class T>
inline void write(T x, char lastChar) {
write(x), push(lastChar);
}
} io;
const int SIZE = 50000 + 5;
int a[SIZE], b[SIZE];
int cnt[SIZE], x;
int l, r, n, m, l0, r0;
signed main() {
io.read(n), io.read(m);
for (int i = 1; i <= n; ++i) io.read(a[i]), b[i] = a[i];
sort(b + 1, b + 1 + n);
int len = unique(b + 1, b + 1 + n) - b - 1;
for (int i = 1; i <= n; ++i) a[i] = lower_bound(b + 1, b + 1 + len, a[i]) - b;
while (m--) {
io.read(l0), io.read(r0);
l = (l0 + x - 1) % n + 1;
r = (r0 + x - 1) % n + 1;
if (l > r) swap(l, r);
for (int i = l; i <= r; ++i) cnt[a[i]]++;
int MAX = 0, pos = 0;
for (int i = 1; i <= len; ++i) if (MAX < cnt[i]) MAX = cnt[i], pos = i;
printf("%d\n", b[pos]);
x = b[pos];
memset(cnt, 0, sizeof cnt);
}
}
19.[CQOI2014]排序机械臂
为了把工厂中高低不等的物品按从低到高排好序,工程师发明了一种排序机械臂。它遵循一个简单的排序规则,第一次操作找到高度最低的物品的位置 \(P_1\) ,并把左起第一个物品至 \(P_1\) 间的物品 (即区间 \([1,P_1]\) 间的物品) 反序;第二次找到第二低的物品的位置 \(P_2\) ,并把左起第二个至 \(P_2\) 间的物品 (即区间 \([2,P_2]\) 间的物品) 反序……最终所有的物品都会被排好序。
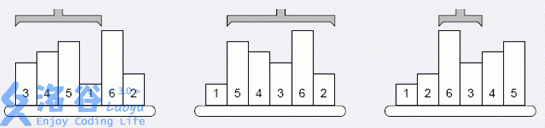
上图给出有六个物品的示例,第一次操作前,高度最低的物品在位置 \(4\) ,于是把第一至第四的物品反序;第二次操作前,第二低的物品在位罝六,于是把第二至六的物品反序……
你的任务便是编写一个程序,确定一个操作序列,即每次操作前第 \(i\) 低的物品所在位置 \(P_i\) ,以便机械臂工作。需要注意的是,如果有高度相同的物品,必须保证排序后它们的相对位置关系与初始时相同。
LYC:
我们乍一看这道题
“哟!区间翻转平衡树裸题,还6倍经验?!”
再一看,每次翻转区间第一个到元素值最小的一个,再删除最小的一个
???
元素值最小的一个
应该怎么维护呢
我们可以在update里顺便维护这个子树中最小的值是第几个和它的大小(我脑残维护了前面有几个数)。
针对这个进行分类讨论:
1).当前结点的值比左右子树的最小值都小
那么最小值是当前结点的值。
它前面的元素个数是左子树的大小(中序遍历为原序列)
2).左子树的最小值最小
完美继承左子树的两个值。
3).右子树的最小值最小
最小值不用说了吧。
它前面的个数就是左子树的大小加一(当前结点)再加上右子树中在它前面的元素个数
因为子树不变时,那我们维护的这个值也不变。子树变了,那就肯定要更新。
然后再每次都查询最小的元素在哪一个位置,删掉它再翻转前面的区间就好了
代码:
#include<cstdio>
#include<algorithm>
using namespace std;
int n,tot,root,root1,root2,root3,c[100010];
struct node
{
int l,r,num,key,sum;
int s,smum;//最小值大小,前面的元素个数
bool rev;//翻转标记
}nodes[100010];
struct laji
{
int v,ID;
}a[100010];
bool cmp(laji one,laji two)
{
if(one.v^two.v) return one.v<two.v;
return one.ID<two.ID;
}//离散化,顺便解决如果值相同,保持原有相对位置的问题
int newnode(int val)
{
nodes[++tot].s=val;//最小值设为自己,前面没有数
nodes[tot].num=val;
nodes[tot].key=rand();
nodes[tot].sum=1;
return tot;
}
void pushdown(int x)
{
swap(nodes[x].l,nodes[x].r);//首先交换左右儿子
nodes[x].smum=nodes[x].sum-(nodes[x].smum+1);//整个子树翻转过来,则最小值的位置就要翻过来
//原来前面的元素个数:nodes[x].smum
//原位置: nodes[x].smum+1
//翻转位置:nodes[x].sum-(nodes[x].smum+1)+1
//翻转后前面的元素个数:nodes[x].sum-(nodes[x].smum+1)
nodes[nodes[x].l].rev^=1;
nodes[nodes[x].r].rev^=1;//下传标记
nodes[x].rev=0;//记得清空
}
void update(int x)
{
nodes[x].sum=nodes[nodes[x].l].sum+nodes[nodes[x].r].sum+1;
if(nodes[nodes[x].l].rev) pushdown(nodes[x].l);
if(nodes[nodes[x].r].rev) pushdown(nodes[x].r);//如果左右子树有标记,也要下传,否则更新出的值不对
if(nodes[x].num<nodes[nodes[x].l].s&&nodes[x].num<nodes[nodes[x].r].s)//分类讨论情况1
{
nodes[x].s=nodes[x].num;
nodes[x].smum=nodes[nodes[x].l].sum;
}
else if(nodes[nodes[x].l].s<nodes[nodes[x].r].s)//情况2
{
nodes[x].s=nodes[nodes[x].l].s;
nodes[x].smum=nodes[nodes[x].l].smum;
}
else//情况3
{
nodes[x].s=nodes[nodes[x].r].s;
nodes[x].smum=nodes[nodes[x].r].smum+nodes[nodes[x].l].sum+1;
}
}
void split(int now,int siz,int &x,int &y)
{
if(!now) x=y=0;
else
{
if(nodes[now].rev) pushdown(now);//下面要用到它的儿子,所以我们要下传标记
if(nodes[nodes[now].l].sum<siz)
{
x=now;
split(nodes[now].r,siz-nodes[nodes[now].l].sum-1,nodes[x].r,y);
}
else
{
y=now;
split(nodes[now].l,siz,x,nodes[y].l);
}
update(now);
}
}
int merge(int x,int y)
{
if(!x||!y) return x+y;
if(nodes[x].key<nodes[y].key)
{
if(nodes[x].rev) pushdown(x);
nodes[x].r=merge(nodes[x].r,y);
update(x);
return x;
}
else
{
if(nodes[y].rev) pushdown(y);
nodes[y].l=merge(x,nodes[y].l);
update(y);
return y;
}
}
int main()
{
srand(20060515);
nodes[0].num=nodes[0].s=1e9;//处理节点为空的特殊情况为极大值,使更新叶子节点时不会把0更新进去
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i].v);
a[i].ID=i;
}
sort(a+1,a+1+n,cmp);
for(int i=1;i<=n;++i) c[a[i].ID]=i;//离散化
for(int i=1;i<=n;++i) root=merge(root,newnode(c[i]));//处理原序列,直接把当前元素插入到它前面元素的右边
for(int i=1;i<=n;++i)
{
if(nodes[root].rev) pushdown(root);//如果根节点有翻转标记要翻转,否则最小值的位置是反的。
printf("%d ",nodes[root].smum+i);//还有之前的i-1个已经被删除的数
split(root,nodes[root].smum,root1,root2);
split(root2,1,root2,root3);//删除这个数
nodes[root1].rev^=1;//翻转前面的区间
root=merge(root1,root3);
}
return 0;
}
WGY:
SplayNB!!!区间操作直接秒过!!(具体题解参考LYC,我就放个代码)
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#define mid ((l + r) >> 1)
using namespace std;
// #define DEBUG 1
struct IO {
#define MAXSIZE (1 << 20)
#define isdigit(x) (x >= '0' && x <= '9')
char buf[MAXSIZE], *p1, *p2;
char pbuf[MAXSIZE], *pp;
#if DEBUG
#else
IO() : p1(buf), p2(buf), pp(pbuf) {}
~IO() { fwrite(pbuf, 1, pp - pbuf, stdout); }
#endif
inline char gc() {
#if DEBUG
return getchar();
#endif
if (p1 == p2) p2 = (p1 = buf) + fread(buf, 1, MAXSIZE, stdin);
return p1 == p2 ? ' ' : *p1++;
}
inline bool blank(char ch) {
return ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t';
}
template <class T>
inline void read(T &x) {
register double tmp = 1;
register bool sign = 0;
x = 0;
register char ch = gc();
for (; !isdigit(ch); ch = gc())
if (ch == '-') sign = 1;
for (; isdigit(ch); ch = gc()) x = x * 10 + (ch - '0');
if (ch == '.')
for (ch = gc(); isdigit(ch); ch = gc())
tmp /= 10.0, x += tmp * (ch - '0');
if (sign) x = -x;
}
inline void read(char *s) {
register char ch = gc();
for (; blank(ch); ch = gc())
;
for (; !blank(ch); ch = gc()) *s++ = ch;
*s = 0;
}
inline void read(char &c) {
for (c = gc(); blank(c); c = gc())
;
}
inline void push(const char &c) {
#if DEBUG
putchar(c);
#else
if (pp - pbuf == MAXSIZE) fwrite(pbuf, 1, MAXSIZE, stdout), pp = pbuf;
*pp++ = c;
#endif
}
template <class T>
inline void write(T x) {
if (x < 0) x = -x, push('-');
static T sta[35];
T top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
while (top) push(sta[--top] + '0');
}
template <class T>
inline void write(T x, char lastChar) {
write(x), push(lastChar);
}
} io;
const int SIZE = 100000 + 5;
struct SPLAY {
int fa;
int size;
int val;
int rev;
int ch[2];
} t[SIZE];
int n, root, tot, pos[SIZE];
struct InputNode {
int id;
int val;
} a[SIZE];
bool cmp1(const InputNode& rhs, const InputNode& rsp) { return rhs.val ^ rsp.val ? rhs.val < rsp.val : rhs.id < rsp.id; }
bool cmp2(const InputNode& rhs, const InputNode& rsp) { return rhs.id < rsp.id; }
void update(int x) {
t[x].size = t[t[x].ch[0]].size + t[t[x].ch[1]].size + 1;
}
void transf(int x) {
if (t[x].rev) {
swap(t[x].ch[0], t[x].ch[1]);
t[t[x].ch[0]].rev ^= 1;
t[t[x].ch[1]].rev ^= 1;
t[x].rev = 0;
}
}
int make(int fa, int l, int r) {
if (l > r) return 0;
int p = ++tot;
return(t[p].val = a[mid].val, t[p].fa = fa, pos[a[mid].val] = p, t[p].ch[0] = make(p, l, mid - 1), t[p].ch[1] = make(p, mid + 1, r), update(p), p);
}
void rotate(int x) {
int y = t[x].fa, z = t[y].fa;
transf(y), transf(x);
int k = t[t[x].fa].ch[1] == x;
t[y].ch[k] = t[x].ch[k ^ 1];
t[t[y].ch[k]].fa = y;
t[y].fa = x;
t[x].ch[k ^ 1] = y;
t[x].fa = z;
if (z) t[z].ch[y == t[z].ch[1]] = x;
update(y), update(x);
}
void splay(int x, int goal) {
for (int y; (y = t[x].fa) ^ goal; rotate(x))
if (t[y].fa ^ goal)
rotate(t[t[x].fa].ch[1] ^ x ^ y ^ t[t[y].fa].ch[1] ? x : y);
if (!goal) root = x;
}
int behavior() {
transf(root);
int x = t[root].ch[1];
while (transf(x), t[x].ch[0]) x = t[x].ch[0];
return x;
}
signed main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i) scanf("%d", &a[i + 1].val), a[i + 1].id = i + 1;
a[1].val = 0, a[n + 2].val = n + 1;
sort(a + 2, a + 2 + n, cmp1);
for (int i = 2; i <= n + 1; ++i) a[i].val = i - 1;
sort(a + 2, a + 2 + n, cmp2);
root = make(0, 1, n + 2);
for (int i = 1; i <= n; ++i) {
int x = pos[i];
splay(x, 0);
printf("%d ", t[t[x].ch[0]].size);
x = behavior();
int y = pos[i - 1];
splay(y, 0);
splay(x, y);
t[t[x].ch[0]].rev ^= 1;
}
return 0;
}
20.[SHOI2013]扇形面积并(权值线段树&扫描线)

给定 n 个同心的扇形,求有多少面积,被至少 \(k\) 个扇形所覆盖。
LYC:
这道题要用到扫描线的思想,那扫描线是什么呢?
扫描线:
经典应用:给出一堆矩阵,求它们覆盖的总面积
数据范围恶心死了,\(10^5\)个矩阵,矩阵的坐标的绝对值小于\(10^9\)。
看到这个数据范围我们就知道:要离散化。
之后呢,我们把每个矩阵的左右边界都转换成添加和删除。
我们用一条扫描线从左到右扫过去,线段树来维护现在整条扫描线的被覆盖情况。
矩阵的左边就是添加以这个矩阵的上下边界点为端点的线段。
右边再右边一个就转换成删除。
每走过一个点,我们就用线段树统计当前扫描线被这些矩阵覆盖了多少,再把答案加上去就好了。
模板我就不写啦其实是我不会
$\ $
好了那我们来看这道题吧。
一堆圆心相同的扇形,求被至少\(k\)个扇形覆盖的面积。
我们先单看一条从圆心射出的射线。
由于每个扇形的圆心是相同的。
所以覆盖每个地方的扇形数量是向外递减的。
那么被至少\(k\)个扇形覆盖的地方就在从外到内第\(k\)个扇形,它被刚好或者多于\(k\)个扇形所覆盖,更向内的地方的数量则更多,也是大于等于\(k\)。
所以我们可以用权值线段树来维护每个地方有多少个扇形边界。从而查找从外到内第\(k\)个扇形边界。
运用扫描线思想,把给出的扇形的两个角度值转换成添加和删除一个扇形边界。
实现有很多坑,自己看注释吧。
代码:
#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
long long n,m,k,nodes[400010],a1,a2,ans,s,now;
struct cir
{
long long r;
bool insorex;//1为添加,2为删除
}cur;
vector<cir> op[2000010];//用来储存在每个角度的修改
void ins(long long l,long long r,long long x,long long pos)
{
++nodes[x];
if(l^r)
{
long long mid=(l+r)>>1;
if(pos<=mid) ins(l,mid,x<<1,pos);
else ins(mid+1,r,x<<1|1,pos);
}
}
void exins(long long l,long long r,long long x,long long pos)//权值线段树删除
{
--nodes[x];
if(l^r)
{
long long mid=(l+r)>>1;
if(pos<=mid) exins(l,mid,x<<1,pos);
else exins(mid+1,r,x<<1|1,pos);
}
}
long long find(long long l,long long r,long long x,long long val)//权值线段树查找从外到内第k个
{
if(l==r) return l;
long long mid=(l+r)>>1;
if(val<=nodes[x<<1|1]) return find(mid+1,r,x<<1|1,val);
else return find(l,mid,x<<1,val-nodes[x<<1|1]);
}
int main()
{
scanf("%lld %lld %lld",&n,&m,&k);
for(long long i=1;i<=n;++i)
{
scanf("%lld %lld %lld",&cur.r,&a1,&a2);
s=max(s,cur.r);
a1+=m;
a2+=m;//a1,a2可能是负数
//转换成添加和修改
if(a1>a2)//这个扇形跨越了分界线,需要拆成两半
{
cur.insorex=1;
op[a1+1].push_back(cur);
op[1].push_back(cur);
cur.insorex=0;
op[a2+1].push_back(cur);
}
else
{
cur.insorex=1;
op[a1+1].push_back(cur);
cur.insorex=0;
op[a2+1].push_back(cur);
}
}
for(long long i=1;i<=m*2;++i)//注意是半开区间(-Pi,Pi]
{
for(long long j=0;j<op[i].size();++j)//进行修改操作
{
cur=op[i][j];
if(cur.insorex)
{
ins(1,s,1,cur.r);
++now;
}
else
{
exins(1,s,1,cur.r);
--now;//统计现在总共有多少个
}
}
if(now>=k)//有k个才统计,不然容易出锅
{
long long tmp=find(1,s,1,k);
ans+=tmp*tmp;//圆面积公式:Pi*r*r
}
}
printf("%lld\n",ans);
return 0;
}
WGY
提供树状数组+二分做法,复杂度\(O(n\log^2n)\)
树状数组写起来短,常数小,动动脑子可以套在很多题目上,它不香嘛
题目让我们求目前覆盖的第 \(k\) 大,我们可以把原来的覆盖位置差分一下,然后二分即可
#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>
#define mid ((l + r) >> 1)
#define mp make_pair
#define fir first
#define sec second
#define pub push_back
#define pob pop_back
using namespace std;
typedef long long LL;
#define DEBUG 1
struct IO {
#define MAXSIZE (1 << 20)
#define isdigit(x) (x >= '0' && x <= '9')
char buf[MAXSIZE], *p1, *p2;
char pbuf[MAXSIZE], *pp;
#if DEBUG
#else
IO() : p1(buf), p2(buf), pp(pbuf) {}
~IO() { fwrite(pbuf, 1, pp - pbuf, stdout); }
#endif
inline char gc() {
#if DEBUG
return getchar();
#endif
if (p1 == p2) p2 = (p1 = buf) + fread(buf, 1, MAXSIZE, stdin);
return p1 == p2 ? ' ' : *p1++;
}
inline bool blank(char ch) {
return ch == ' ' || ch == '\n' || ch == '\r' || ch == '\t';
}
template <class T>
inline void read(T &x) {
register double tmp = 1;
register bool sign = 0;
x = 0;
register char ch = gc();
for (; !isdigit(ch); ch = gc())
if (ch == '-') sign = 1;
for (; isdigit(ch); ch = gc()) x = x * 10 + (ch - '0');
if (ch == '.')
for (ch = gc(); isdigit(ch); ch = gc())
tmp /= 10.0, x += tmp * (ch - '0');
if (sign) x = -x;
}
inline void read(char *s) {
register char ch = gc();
for (; blank(ch); ch = gc())
;
for (; !blank(ch); ch = gc()) *s++ = ch;
*s = 0;
}
inline void read(char &c) {
for (c = gc(); blank(c); c = gc())
;
}
inline void push(const char &c) {
#if DEBUG
putchar(c);
#else
if (pp - pbuf == MAXSIZE) fwrite(pbuf, 1, MAXSIZE, stdout), pp = pbuf;
*pp++ = c;
#endif
}
template <class T>
inline void write(T x) {
if (x < 0) x = -x, push('-');
static T sta[35];
T top = 0;
do {
sta[top++] = x % 10, x /= 10;
} while (x);
while (top) push(sta[--top] + '0');
}
template <class T>
inline void write(T x, char lastChar) {
write(x), push(lastChar);
}
} io;
const int SIZE = 1e6 + 5;
int n, m, k, a[SIZE];
LL tree[SIZE], ans;
vector < int > In[SIZE<<1], Out[SIZE<<1];
void Add(int x, int y) { for (; x < SIZE; x += x & -x) tree[x] += y; }
int Ask(int x, int res = 0) { for (; x; x -= x & -x) res += tree[x]; return res; }
int KthElement(int k) {
int l = 1, r = SIZE - 5;
while (l < r)
if (Ask(mid) < k) l = mid + 1;
else r = mid;
return l;
}
signed main() {
io.read(m), io.read(n), io.read(k);
int L, R;
for (int i = 1; i <= m; ++i) {
io.read(a[i]);
io.read(L);
io.read(R);
if (L < R) L += n + 1, R += n, In[L].pub(i), Out[R + 1].pub(i);
else L ^= R ^= L ^= R, L += n, R += n + 1, In[1].pub(i), Out[L + 1].pub(i), In[R].pub(i);
}
int now = 0, x;
for (int i = 1; i <= (n<<1); ++i) {
for (int j = 0; j < In[i].size(); ++j) Add(a[In[i][j]], 1);
for (int j = 0; j < Out[i].size(); ++j) Add(a[Out[i][j]], -1);
now += In[i].size() - Out[i].size();
if (now >= k) x = KthElement(now - k + 1), ans += (LL)x * x;
}
printf("%lld\n", ans);
return 0;
}

