Solution -「洛谷 P5659」「CSP-S 2019」树上的数

Description

Link.

联赛原题应该都读过吧……

Solution

Part 0

大致思路

主要的思路就是逐个打破，研究特殊的数据得到普通的结论。

Part 1

暴力的部分分

暴力的部分分很好拿，我们可以直接把全排列，然后 \(\Theta(n)\) 判断更新答案。

~~恭喜您拿到赛场满分~~

namespace SubtaskForce {
	int cmp[MAXN], ans[MAXN];
	bool vis[MAXN];
	void dfs(int now) { // 全排列
		if (now == n) { // 更新答案
			for (R int i = 1; i <= n; ++i) cmp[id[i]] = i;
			for (R int i = 1; i <= n; ++i) {
				if (cmp[i] < ans[i]) {
					for (R int j = 1; j <= n; ++j) ans[j] = cmp[j];
					break;
				}
				if (cmp[i] > ans[i]) break;
			}
			return ;
		}
		for (R int i = 1; i < n; ++i) {
			if (!vis[i]) {
				vis[i] = 1;
				swap(id[nodes[i].x], id[nodes[i].y]);
				dfs(now + 1);
				swap(id[nodes[i].x], id[nodes[i].y]);
				vis[i] = 0;
			}
		}
	}

	void main() { // 初始化
		for (R int i = 1; i <= n; ++i) vis[i] = 0;
		for (R int i = 1; i <= n; ++i) ans[i] = n - i + 1;
		dfs(1);
		for (R int i = 1; i <= n; ++i) printf("%d ", ans[i]);
		puts("");
	}
}

Part 2

菊花图的部分分

就这道题而言，菊花图其实是比链的数据好想一些的。

我们称菊花图中度数为 \(n-1\) 的结点为 \(rt\) 罢。

我们可以发现在菊花图上删除边一定是某个结点和 \(rt\) 之间。

也就是说无论我们按怎样的顺序删边，最后都会变成一个环。

我做了一个动图演示，如果洛谷博客不支持gif的话就直接到这个网址 Click Here

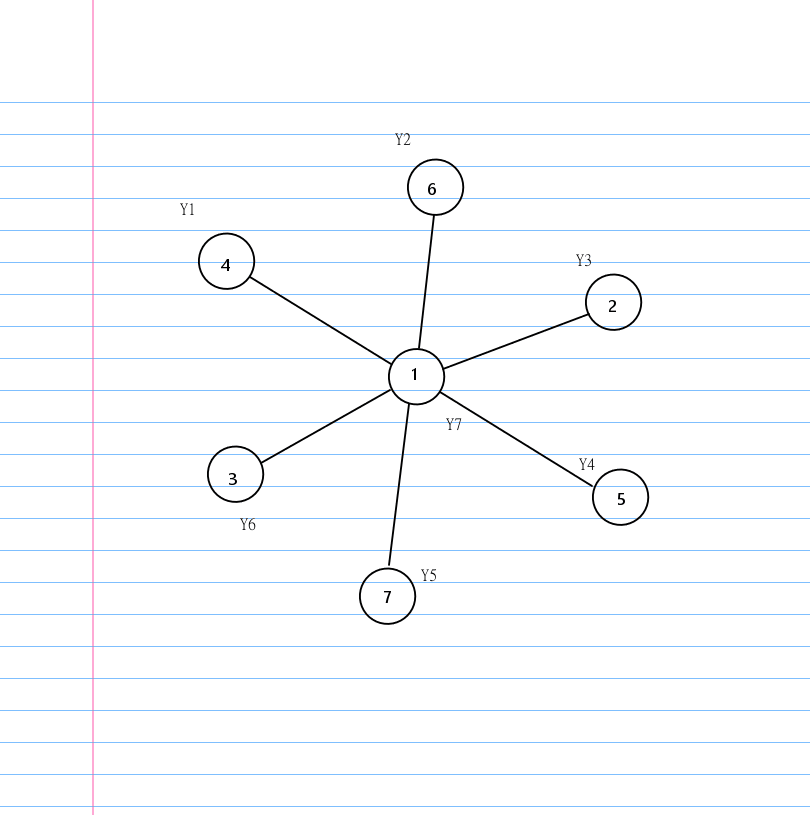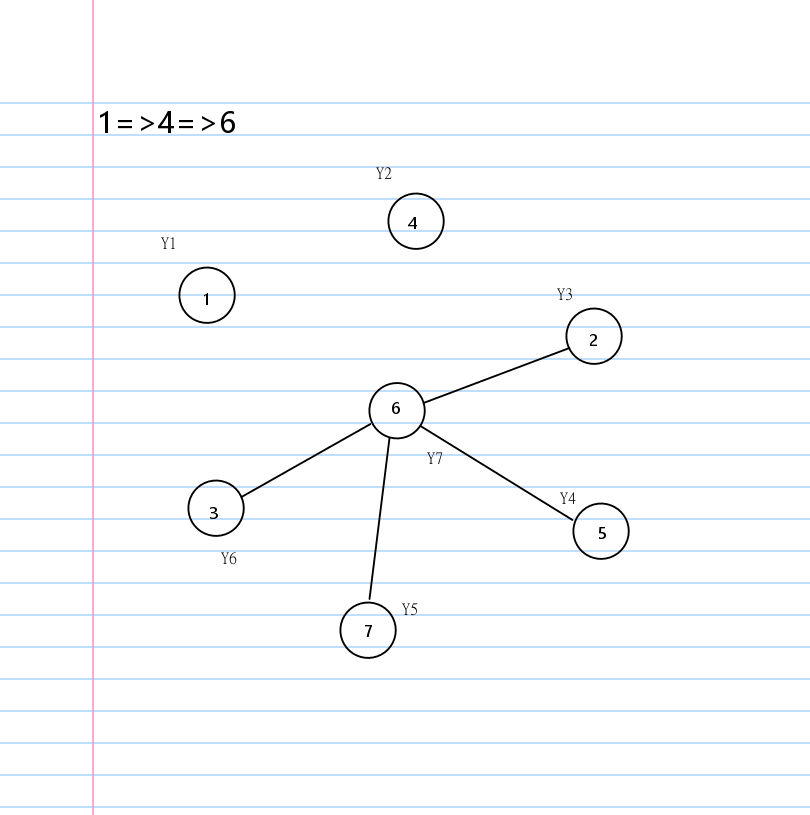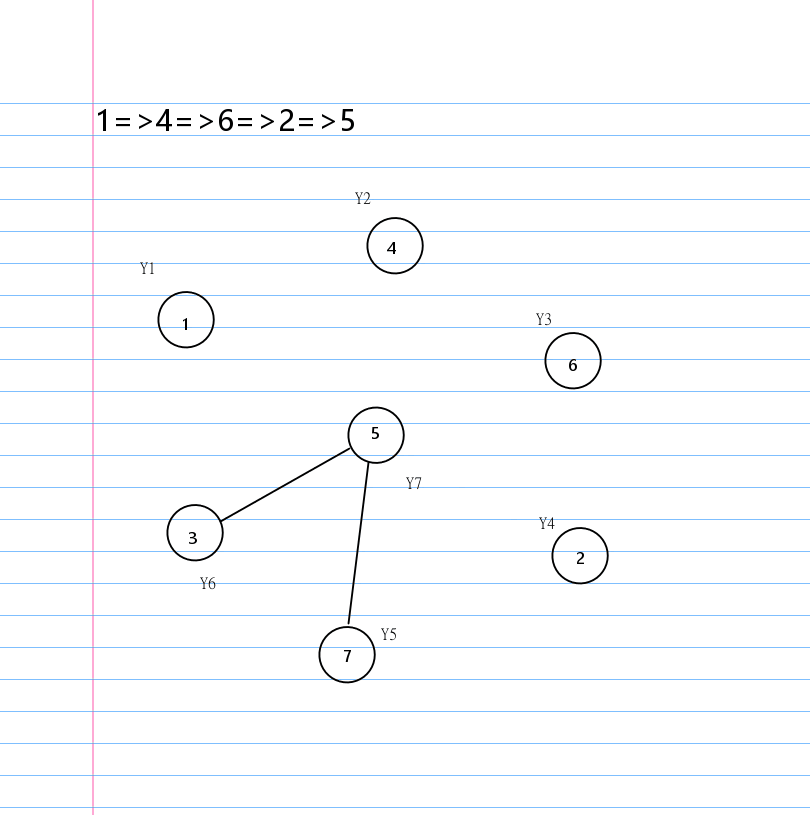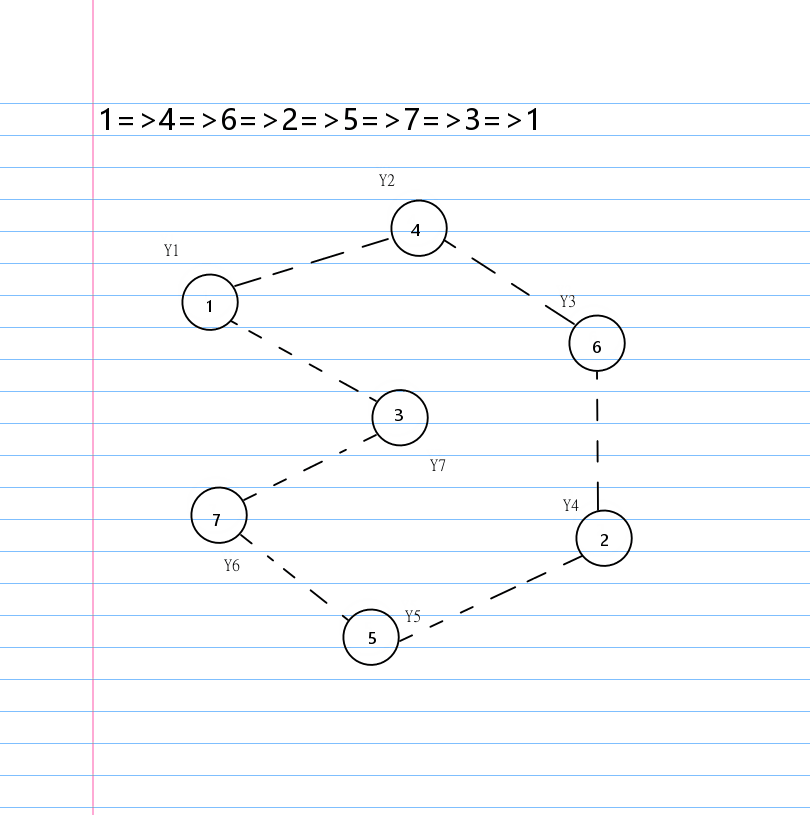
有了环这个结论，就有一个很显然的贪心构造环的方法：

按照 \(1,2,\cdots,n\) 的顺序每个数字选择环上自己的下一个点。

在编写代码的时候还需要注意还没有连到 \(Y_{n}\) 就提前自毙自闭封闭的情况。

namespace SubtaskAss { // 菊花的单词太长了，就取了个差不多的/xyx
	bool vis[MAXN];
	int ans[MAXN];
	struct UninoFindSet {
		int fa[MAXN];

		void init(int limit) {
			for (R int i = 1; i <= limit; ++i)
				fa[i] = i;
		}

		int find(int x) {
			if (x ^ fa[x]) fa[x] = find(fa[x]);
			return fa[x];
		}

		void merge(int x, int y) {
			x = find(x);
			y = find(y);
			if (x ^ y) fa[x] = y;
		}
	} ufs;

	void main() {
		ufs.init(n);
		for (R int i = 1; i <= n; ++i) vis[i] = 0;
		for (R int i = 1; i <= n; ++i) {
			for (R int j = 1; j <= n; ++j) {
				if (!vis[j] && (i == n || ufs.find(j) != ufs.find(id[i]))) {
					vis[j] = 1;
					ans[i] = j;
					ufs.merge(j, id[i]);
					break;
				}
			}
		}
		for (R int i = 1; i <= n; ++i) printf("%d ", ans[i]);
		puts("");
	}
}

Part 3

链的部分分

说实话链的部分分其实也挺好拿的，但是还是比菊花图难想一些。

首先，用dfs序把链拍成树是固定操作了。

链有一个性质，就是每个结点(两端点除外)的度数都有且只有二。

也就是说除端点外，每个结点都有两条边。而且这两条边的被删除时间一定不一样（废话

也就是说每个结点的两条边被删除的情况一共有三种。

我们定义 \(order_{i}\) 为结点 \(i\) 的左右两边的删除情况：

0：0表示这个结点的左右边都还没被删除
1：1表示这个结点的左边先被删除
2：2表示这个结点的右边先被删除

现在我们假设左边的结点 \(u\) 要跑到右边的结点 \(v\) 那里去，那么在 \(u\) 和 \(v\) 之间的结点一定是左边先被删除，所以 \(order_i=1,i\in (u,v)\)

对于 \(u\) 和 \(v\) 两个结点，一定是右边先被删除，否则就不知道跑哪里去了

所以 \(order_{u}=order_{v}=2\)

至于从右跑到左就完全同理了。

答案则同样是从小枚举到大(我是从小枚举到大的/xyx)

比如说我们当前枚举到了结点 \(x\)，我们希望它能去尽量小的一个点

假设当前 \(x\) 在 \(P_{x}\)，我们直接暴力枚举一个 \(P_{y}\)。

判断一个方案是否可行只需要判断它与前面的删边顺序冲突即可。

这样做是 \(\Theta(N^3)\) 的。我们可以在dfs的时候标记，这样就是 \(\Theta(n^2)\) 了。

namespace SubtaskChain {
	int rnk[MAXN], ans[MAXN], dfn[MAXN];
	int sbc_tot, order[MAXN], vis[MAXN];

	void dfs(int x, int fa) {
		rnk[dfn[x] = ++sbc_tot] = x;
		for (R int i = head[x]; i; i = nxt[i])
			if (to[i] ^ fa) dfs(to[i], x);
	}

	void mark_node(int p1, int p2, int tg) {
		if (p1 != 1 && p1 != n) order[p1] = tg + 1;
		if (p2 != 1 && p2 != n) order[p2] = tg + 1;
		for (R int i = (tg ? p1 + 1 : p2 + 1); i < (tg ? p2 : p1); ++i) order[i] = ((tg ^ 1) + 1);
	}

	int iterate(int x, int tg) {
		int res = n + 1;
		if (order[dfn[x]] == tg + 1) return res;
		for (R int i = dfn[x] + (tg ? -1 : 1); tg ? (i >= 1) : (i <= n); i += (tg ? -1 : 1)) {
			if (order[i] == (tg ^ 1) + 1) {
				if (!vis[i]) res = min(res, rnk[i]);
				break;
			}
			if (!order[i] && !vis[i]) res = min(res, rnk[i]);
		}
		return res;
	}
    int inver_id[MAXN];
	void main() {
		for (R int i = 1; i <= n; ++i) rnk[i] = 0;
		for (R int i = 1; i <= n; ++i) dfn[i] = 0;
		for (R int i = 1; i <= n; ++i) vis[i] = 0;
		for (R int i = 1; i <= n; ++i) order[i] = 0;
		for (R int i = 1; i <= n; ++i) inver_id[id[i]] = i;
		sbc_tot = 0;
		for (R int i = 1; i <= n; ++i) {
			if (in[i] == 1) {
				dfs(i, 0);
				break;
			}
		}
		for (R int i = 1; i <= n; ++i) {
			int left = iterate(inver_id[i], 1);
			int right = iterate(inver_id[i], 0);
			if (left < right) mark_node(dfn[inver_id[i]], dfn[left], 0);
			else left = right, mark_node(dfn[inver_id[i]], dfn[left], 1);
			ans[i] = left;
			vis[dfn[left]] = 1;
		}
		for (R int i = 1; i <= n; ++i) printf("%d ", ans[i]);
		puts("");
	}
}

Part 4

正解

~~拼凑出的正解~~

（我能说这剩下的40pts我看题解都看了半天吗）

剩下的40pts是我看了这篇题解才会的Click Here

其实会了链的数据基本就离成功不远了。

仔细想想，我们在处理链的时候，规定了与一个结点的边的删除顺序的数值。

如果放到一般的情况来看，我们可以确定一个类似于拓扑序的删除顺序，即某一条边需要在某一条边删除过后才能被删除。

比如下图：

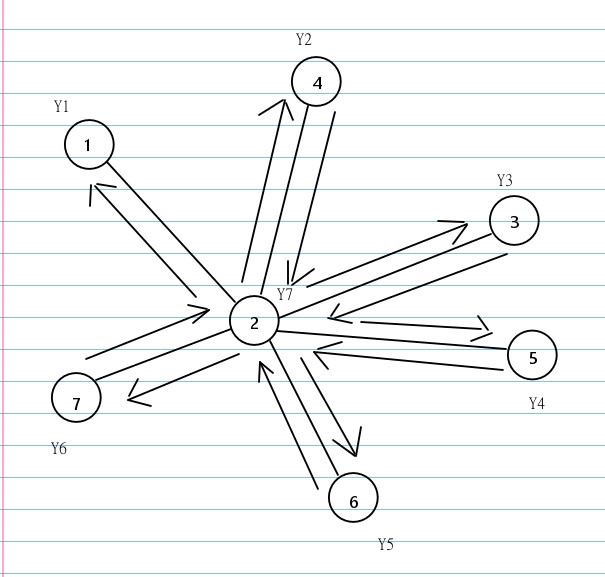
当我们把这一删除顺序写出来，就可以发现这其实构成了一个链。

对吧！对吧！

假设我们现在需要把 \(x\) 删到 \(y\) 结点上。

那么判断法则如下：

不合法的情况：

有一个数已经从 \(x\) 出去过了
有一个数已经到过 \(y\) 这里了
有一个数从相同方向过了 \(x\) 的一条出边
有一个数从相同方向过了 \(y\) 的一条出边
出/入边任意一条被别的数字从相同方向走了一次
加上当前数构成的链 \(x\) 有任意一边出边不在上面
加上当前数构成的链 \(y\) 有任意一边出边不在上面
加上当前数后，经过 \(x\) 的数字自闭了(形成了一个环)
加上当前数后，形成了一条链，\(x\) 有任意一条出边不在上面

合法的情况

排除以上所有情况即合法

直接贪心会死得很惨烈。

我们可以通过dfs找出编号最小的作为本轮的答案。

namespace SubtaskRandom {
	int mark[MAXN][MAXN], inver_id[MAXN];
	int lave_unwalked[MAXN], fa[MAXN];
	int lave_in[MAXN], lave_out[MAXN];
	int node_from[MAXN], node_to[MAXN];
	int header[MAXN][MAXN], footer[MAXN][MAXN];
	bool vis[MAXN];

	void dfs(int x, int rt) {
		for (R int i = head[x]; i; i = nxt[i]) {
			int y = to[i];
			if (y ^ fa[x]) {
				fa[y] = x;
				vis[y] = 1;
				if (x ^ rt) {
					if (mark[x][y] == x || mark[fa[x]][x] == fa[x]) vis[y] = 0;
					if (mark[x][y] == 0 || mark[fa[x]][x] == 0) vis[y] = 0;
					if (header[x][fa[x]] == node_to[x] && footer[x][y] == node_from[x]
						&& lave_out[x] + lave_in[x] + (lave_unwalked[x] << 1) > 2) vis[y] = 0;
					if (footer[x][y] == fa[x]) vis[y] = 0;
				}
				else {
					if (mark[x][y] == x) vis[y] = 0;
					if (mark[x][y] == 0) vis[y] = 0;
					if (node_from[x]) {
						if (footer[x][y] == node_from[x] && lave_unwalked[x] + lave_in[x] + lave_out[x] != 1)
							vis[y] = 0;
					}
				}
				vis[y] &= vis[x];
				dfs(y, rt);
			}
		}
		if (rt ^ x) {
			if (node_from[x]) vis[x] = 0;
			if (node_to[x]) {
				if (footer[x][node_to[x]] == fa[x] && lave_unwalked[x] + lave_in[x] + lave_out[x] != 1)
					vis[x] = 0;
			}
		}
		else {
			vis[x] = 0;
		}
	}

	void main() {
		for (R int i = 1; i <= n; ++i) node_from[i] = 0;
		for (R int i = 1; i <= n; ++i) node_to[i] = 0;
		for (R int i = 1; i <= n; ++i) lave_in[i] = 0;
		for (R int i = 1; i <= n; ++i) lave_out[i] = 0;
		for (R int i = 1; i <= n; ++i) lave_unwalked[i] = 0;
		for (R int i = 1; i <= n; ++i) inver_id[id[i]] = i;
		for (R int i = 1; i < n; ++i) {
			lave_unwalked[nodes[i].x]++;
			lave_unwalked[nodes[i].y]++;
			mark[nodes[i].x][nodes[i].y] = -1;
			mark[nodes[i].y][nodes[i].x] = -1;
			header[nodes[i].x][nodes[i].y] = nodes[i].y;
			header[nodes[i].y][nodes[i].x] = nodes[i].x;
			footer[nodes[i].x][nodes[i].y] = nodes[i].y;
			footer[nodes[i].y][nodes[i].x] = nodes[i].x;
		}
		for (R int i = 1; i <= n; ++i) {
			for (R int j = 1; j <= n; ++j) fa[j] = 0;
			vis[inver_id[i]] = 1;
			dfs(inver_id[i], inver_id[i]);
			int res = 0;
			for (R int j = 1; j <= n; ++j) {
				if (vis[j]) {
					res = j;
					break;
				}
			}
			printf("%d ", res);
			node_from[res] = fa[res];
			while (fa[res] ^ inver_id[i]) {
				if (~mark[fa[res]][res]) {
					mark[fa[res]][res] = mark[res][fa[res]] = 0;
					lave_in[res]--;
					lave_out[fa[res]]--;
				}
				else {
					mark[fa[res]][res] = mark[res][fa[res]] = fa[res];
					lave_unwalked[res]--;
					lave_out[res]++;
					lave_unwalked[fa[res]]--;
					lave_in[fa[res]]++;
				}
				int t = res;
				res = fa[res];
				header[res][footer[res][t]] = header[res][fa[res]];
				footer[res][header[res][fa[res]]] = footer[res][t];
			}
			if (~mark[fa[res]][res]) {
				mark[fa[res]][res] = 0;
				mark[res][fa[res]] = 0;
				lave_in[res]--;
				lave_out[inver_id[i]]--;
			}
			else {
				mark[fa[res]][res] = fa[res];
				mark[res][fa[res]] = fa[res];
				lave_unwalked[res]--;
				lave_out[res]++;
				lave_unwalked[inver_id[i]]--;
				lave_in[inver_id[i]]++;
			}
			node_to[inver_id[i]] = res;
		}
		puts("");
	}
}

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cstring>
#include <queue>

using namespace std;

char buf[1 << 21], *p1 = buf, *p2 = buf;
#ifndef ONLINE_JUDGE
#define gc() getchar()
#else
#define gc() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 21, stdin), p1 == p2) ? EOF : *p1++)
#endif
#define is() (ch >= '0' && ch <= '9')
#define R register

template < class Type >
void read(Type& a) {
	a = 0; bool f = 0; char ch;
	while (!(ch = gc(), is())) if (ch == '-') f = 1;
	while (is()) a = (a << 3) + (a << 1) + (ch ^ '0'), ch = gc();
	a = (f ? -a : a);
}

template < class Type, class... Args >
void read(Type& t, Args&... args) {
	read(t), read(args...);
}

const int MAXN = 2000 + 5;
int T, n, max_in, id[MAXN];
int head[MAXN], nxt[MAXN << 1];
int tot, in[MAXN], to[MAXN << 1];
struct EdgeNode {
	int x, y;
} nodes[MAXN];

EdgeNode make_edge(int x, int y) {
	EdgeNode res;
	res.x = x;
	res.y = y;
	return res;
}

void add(int x, int y) {
	to[++tot] = y;
	nxt[tot] = head[x];
	head[x] = tot;
}

namespace SubtaskForce {
	int cmp[MAXN], ans[MAXN];
	bool vis[MAXN];
	void dfs(int now) {
		if (now == n) {
			for (R int i = 1; i <= n; ++i) cmp[id[i]] = i;
			for (R int i = 1; i <= n; ++i) {
				if (cmp[i] < ans[i]) {
					for (R int j = 1; j <= n; ++j) ans[j] = cmp[j];
					break;
				}
				if (cmp[i] > ans[i]) break;
			}
			return ;
		}
		for (R int i = 1; i < n; ++i) {
			if (!vis[i]) {
				vis[i] = 1;
				swap(id[nodes[i].x], id[nodes[i].y]);
				dfs(now + 1);
				swap(id[nodes[i].x], id[nodes[i].y]);
				vis[i] = 0;
			}
		}
	}

	void main() {
		for (R int i = 1; i <= n; ++i) vis[i] = 0;
		for (R int i = 1; i <= n; ++i) ans[i] = n - i + 1;
		dfs(1);
		for (R int i = 1; i <= n; ++i) printf("%d ", ans[i]);
		puts("");
	}
}

namespace SubtaskAss {
	bool vis[MAXN];
	int ans[MAXN];
	struct UninoFindSet {
		int fa[MAXN];

		void init(int limit) {
			for (R int i = 1; i <= limit; ++i)
				fa[i] = i;
		}

		int find(int x) {
			if (x ^ fa[x]) fa[x] = find(fa[x]);
			return fa[x];
		}

		void merge(int x, int y) {
			x = find(x);
			y = find(y);
			if (x ^ y) fa[x] = y;
		}
	} ufs;

	void main() {
		ufs.init(n);
		for (R int i = 1; i <= n; ++i) vis[i] = 0;
		for (R int i = 1; i <= n; ++i) {
			for (R int j = 1; j <= n; ++j) {
				if (!vis[j] && (i == n || ufs.find(j) != ufs.find(id[i]))) {
					vis[j] = 1;
					ans[i] = j;
					ufs.merge(j, id[i]);
					break;
				}
			}
		}
		for (R int i = 1; i <= n; ++i) printf("%d ", ans[i]);
		puts("");
	}
}

namespace SubtaskChain {
	int rnk[MAXN], ans[MAXN], dfn[MAXN];
	int sbc_tot, order[MAXN], vis[MAXN];

	void dfs(int x, int fa) {
		rnk[dfn[x] = ++sbc_tot] = x;
		for (R int i = head[x]; i; i = nxt[i])
			if (to[i] ^ fa) dfs(to[i], x);
	}

	void mark_node(int p1, int p2, int tg) {
		if (p1 != 1 && p1 != n) order[p1] = tg + 1;
		if (p2 != 1 && p2 != n) order[p2] = tg + 1;
		for (R int i = (tg ? p1 + 1 : p2 + 1); i < (tg ? p2 : p1); ++i) order[i] = ((tg ^ 1) + 1);
	}

	int iterate(int x, int tg) {
		int res = n + 1;
		if (order[dfn[x]] == tg + 1) return res;
		for (R int i = dfn[x] + (tg ? -1 : 1); tg ? (i >= 1) : (i <= n); i += (tg ? -1 : 1)) {
			if (order[i] == (tg ^ 1) + 1) {
				if (!vis[i]) res = min(res, rnk[i]);
				break;
			}
			if (!order[i] && !vis[i]) res = min(res, rnk[i]);
		}
		return res;
	}
    int inver_id[MAXN];
	void main() {
		for (R int i = 1; i <= n; ++i) rnk[i] = 0;
		for (R int i = 1; i <= n; ++i) dfn[i] = 0;
		for (R int i = 1; i <= n; ++i) vis[i] = 0;
		for (R int i = 1; i <= n; ++i) order[i] = 0;
		for (R int i = 1; i <= n; ++i) inver_id[id[i]] = i;
		sbc_tot = 0;
		for (R int i = 1; i <= n; ++i) {
			if (in[i] == 1) {
				dfs(i, 0);
				break;
			}
		}
		for (R int i = 1; i <= n; ++i) {
			int left = iterate(inver_id[i], 1);
			int right = iterate(inver_id[i], 0);
			if (left < right) mark_node(dfn[inver_id[i]], dfn[left], 0);
			else left = right, mark_node(dfn[inver_id[i]], dfn[left], 1);
			ans[i] = left;
			vis[dfn[left]] = 1;
		}
		for (R int i = 1; i <= n; ++i) printf("%d ", ans[i]);
		puts("");
	}
}

namespace SubtaskRandom {
	int mark[MAXN][MAXN], inver_id[MAXN];
	int lave_unwalked[MAXN], fa[MAXN];
	int lave_in[MAXN], lave_out[MAXN];
	int node_from[MAXN], node_to[MAXN];
	int header[MAXN][MAXN], footer[MAXN][MAXN];
	bool vis[MAXN];

	void dfs(int x, int rt) {
		for (R int i = head[x]; i; i = nxt[i]) {
			int y = to[i];
			if (y ^ fa[x]) {
				fa[y] = x;
				vis[y] = 1;
				if (x ^ rt) {
					if (mark[x][y] == x || mark[fa[x]][x] == fa[x]) vis[y] = 0;
					if (mark[x][y] == 0 || mark[fa[x]][x] == 0) vis[y] = 0;
					if (header[x][fa[x]] == node_to[x] && footer[x][y] == node_from[x]
						&& lave_out[x] + lave_in[x] + (lave_unwalked[x] << 1) > 2) vis[y] = 0;
					if (footer[x][y] == fa[x]) vis[y] = 0;
				}
				else {
					if (mark[x][y] == x) vis[y] = 0;
					if (mark[x][y] == 0) vis[y] = 0;
					if (node_from[x]) {
						if (footer[x][y] == node_from[x] && lave_unwalked[x] + lave_in[x] + lave_out[x] != 1)
							vis[y] = 0;
					}
				}
				vis[y] &= vis[x];
				dfs(y, rt);
			}
		}
		if (rt ^ x) {
			if (node_from[x]) vis[x] = 0;
			if (node_to[x]) {
				if (footer[x][node_to[x]] == fa[x] && lave_unwalked[x] + lave_in[x] + lave_out[x] != 1)
					vis[x] = 0;
			}
		}
		else {
			vis[x] = 0;
		}
	}

	void main() {
		for (R int i = 1; i <= n; ++i) node_from[i] = 0;
		for (R int i = 1; i <= n; ++i) node_to[i] = 0;
		for (R int i = 1; i <= n; ++i) lave_in[i] = 0;
		for (R int i = 1; i <= n; ++i) lave_out[i] = 0;
		for (R int i = 1; i <= n; ++i) lave_unwalked[i] = 0;
		for (R int i = 1; i <= n; ++i) inver_id[id[i]] = i;
		for (R int i = 1; i < n; ++i) {
			lave_unwalked[nodes[i].x]++;
			lave_unwalked[nodes[i].y]++;
			mark[nodes[i].x][nodes[i].y] = -1;
			mark[nodes[i].y][nodes[i].x] = -1;
			header[nodes[i].x][nodes[i].y] = nodes[i].y;
			header[nodes[i].y][nodes[i].x] = nodes[i].x;
			footer[nodes[i].x][nodes[i].y] = nodes[i].y;
			footer[nodes[i].y][nodes[i].x] = nodes[i].x;
		}
		for (R int i = 1; i <= n; ++i) {
			for (R int j = 1; j <= n; ++j) fa[j] = 0;
			vis[inver_id[i]] = 1;
			dfs(inver_id[i], inver_id[i]);
			int res = 0;
			for (R int j = 1; j <= n; ++j) {
				if (vis[j]) {
					res = j;
					break;
				}
			}
			printf("%d ", res);
			node_from[res] = fa[res];
			while (fa[res] ^ inver_id[i]) {
				if (~mark[fa[res]][res]) {
					mark[fa[res]][res] = mark[res][fa[res]] = 0;
					lave_in[res]--;
					lave_out[fa[res]]--;
				}
				else {
					mark[fa[res]][res] = mark[res][fa[res]] = fa[res];
					lave_unwalked[res]--;
					lave_out[res]++;
					lave_unwalked[fa[res]]--;
					lave_in[fa[res]]++;
				}
				int t = res;
				res = fa[res];
				header[res][footer[res][t]] = header[res][fa[res]];
				footer[res][header[res][fa[res]]] = footer[res][t];
			}
			if (~mark[fa[res]][res]) {
				mark[fa[res]][res] = 0;
				mark[res][fa[res]] = 0;
				lave_in[res]--;
				lave_out[inver_id[i]]--;
			}
			else {
				mark[fa[res]][res] = fa[res];
				mark[res][fa[res]] = fa[res];
				lave_unwalked[res]--;
				lave_out[res]++;
				lave_unwalked[inver_id[i]]--;
				lave_in[inver_id[i]]++;
			}
			node_to[inver_id[i]] = res;
		}
		puts("");
	}
}

signed main() {
	for (read(T); T; --T) {
		read(n);
		for (R int i = 1, x; i <= n; ++i) read(x), id[x] = i;
		for (R int i = 1; i <= n; ++i) head[i] = in[i] = 0;
		tot = 0, max_in = 0;
		for (R int i = 1; i < n; ++i) {
			int x, y;
			read(x, y);
			add(x, y);
			add(y, x);
			++in[x], ++in[y];
			nodes[i] = make_edge(x, y);
			max_in = max(max_in, max(in[x], in[y]));
		}
		if (n <= 10) SubtaskForce::main();
		else if (max_in == n - 1) SubtaskAss::main();
		else if (max_in == 2) SubtaskChain::main();
		else SubtaskRandom::main();
	}
}

posted @ 2020-04-19 12:49 cirnovsky 阅读(326) 评论(0) 编辑收藏举报

刷新页面返回顶部

𝒸𝒾𝓇𝓃ℴ𝓋𝓈𝓀𝓎