自动机理论、语言和计算导论：笔记

Automata Theory, Languages, and Computation

中间有一大部分内容，都因为笔记本意外关闭，没有保存而丢失了，实在是可惜。但也回不到那时候的劲头去再敲一遍笔记了

Automata Theory, Languages, and Computation

Sec2 Finite Automata

2.1 Informal Picture of Finite Automata

The Ground Rules
The Protocol
Enabling the Automata to Ignore Actions
The Entire System as an Automaton
- Product Automaton

2.2 Deterministic Finite Automata

2.2.1 Definition of DFA

Formal definition:

\[A = (Q, \Sigma, \delta, q_0, F) \]
1. A finite set of states, often denoted $Q$
2. A finite set of input symbols, often denoted $\Sigma$
3. A transition function that takes as arguments a state and an input symbol and returns a state The transition function will commonly be denoted $\delta$
4. A start state one of the states in $Q$, denoted $q_0$
5. A set of final or accepting states $F$. The set $F$ is a subset of $Q$

2.2.3 Simpler Notations for DFA’s

Transition diagram
Transition table

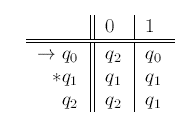
2.2.4 Extending the Transition Function to Strings

Assume that $w = xa$
\[\hat{\delta}(q,w) = \delta(\hat{\delta}(q,x),a) \]

2.2.5 The Language of a DFA

Language:
\[L(A) = \{w,|\hat{\delta}(q_0,w)\in F\} \]

2.3 Nondeterministic Finite Automata

2.3.2 Formal Definition of NFA’s

Definition by set:

\[A = (Q,\Sigma,\delta,q_0,F) \]
1. $Q,\Sigma,q_0,F$ is the same as DFA’s, representing finite set, input symbols, start state and accepting states set respectively.
2. $\delta$, the transition function returns a subset of $Q$.

2.3.3 Extended Transition Function

Definition:
- BASIS:
  $\hat{\delta}(q,\epsilon)={q}$.
- INDUCTION:
  Suppose $w$ is of the form $w=xa$, where $a$ is the final symbol of $w$. Also suppose that $\hat{\delta}(q,x)={p_1,p_2,\dots,p_k}$.
  Let:
  
  \[\bigcup_{i=1}^k\delta(p_i,a) = \{r_1,r_2,\dots,r_m\} \]
  Then $\hat{\delta}(q,w)={r_1,r_2,\dots,r_m}$.

2.3.4 The Language of an NFA

Definition:
\[L(A) = \{w|\hat{\delta}(q_0,w)\cap F \ne\empty\} \]

2.3.5 Equivalence of Deterministic and Nondeterministic Finite Automata

Subset construction
$NFA\ N = (Q_N,\Sigma,\delta_N,q_0,F_N)$ --> $DFA\ D=(Q_D,\Sigma,\delta_D,\{q_0\},F_D)$
Such that $L(D)=L(N)$
- Steps:
  1. $Q_D$ is the set of subsets of $Q_N$
  2. $F_D$ is the set of subsets $S$ of $ Q_N$ such that $S\cap F_N\ne\empty $
  3. For each set $S\subseteq Q_N$ and for each input symbol $a$ in $\Sigma$
    
    \[\delta_D(S,a) = \bigcup_{p\ in\ S}\delta_D(p,a) \]

2.3.6 A Bad Case for the Subset Construction

Worst Case for Subset Construction
If we have to track every state in NFA, there will be $2^n$ states for DFA.
The Pigeonhole Principle

2.5 Finite Automata With Epsilon-Transitions

2.5.2 The Formal Notation for an ε-NFA

Notation:

\[A=(Q,\Sigma,\delta,q_0,F) \]
- all components have their same interpretation as for an NFA except that $\delta$ is now a function that takes as arguments:
  1. A state in $Q$, and
  2. A member of $\Sigma \cup\{\epsilon\}$ , that is either an input symbol or the symbol $\epsilon$ .
    We require that $\epsilon$ the symbol for the empty string cannot be a member of the alphabet $\Sigma$, so no confusion results.

2.5.3 Epsilon-Closures

Definition of Epsilon-Closure:
- BASIS:
  State $q $ is in $ECLOSE(q)$
- INDUCTION:
  If state $p$ is in $ECLOSE(q)$ and there is a transition from state $p$ to state $r$ labeled $\epsilon$, then $r$ is in $ECLOSE(q)$.
  More precisely, if $\delta$ is the transition function of the $\epsilon-NFA$ involved, and $p $ is in $ECLOSE(q)$, then $ECLOSE(q)$ also
  contains all the states in $\delta(p,\epsilon)$

2.5.4 Extended Transitions and Languages for ε-NFA’s

Languages:
\[L(E) = \{w|\hat{\delta}(q_0,w)\cap F \ne\empty\} \]

2.5.5 Eliminating Epsilon-Transition

Let $E=(Q_E,\Sigma,\delta_E,q_0,F_E)$, then the equivalent $DFA$

\[D = (Q_D,\Sigma,\delta_D,q_D,F_D) \]

Step:
1. $Q_D$ is the set of subsets of $Q_E$. More precisely, all accessible states of $D$ are $\epsilon-closed$ subsets of $Q_E$.
2. $q_D=ECLOSE(q_0)$
3. $F_D$ is those sets of states that contain at least one accepting state of $E$. That is
  
  \[F_D = \{S|S\ is\ in\ Q_D\ and\ S\cap F_E\ne \empty\} \]
4. $\delta_D(S,a)$ is computed, for all $a$ in $\Sigma$ and sets $S$ in $Q_D$ by:
  - Let $S=\{p_1,p_2,\dots,p_k\}$
  - Compute $\bigcup_{i=1}^{k}\delta_E(p_i,a)$; Let this set be $\{r_1,r_2,\dots,r_m\}$
  - Then $\delta_D(S,a)=ECLOSE(\{r_1,r_2,\dots,r_m\})$

Sec3 Regular Expressions and Languages

3.1 Regular Expressions

3.1.1 The Operators of Regular Expressions

union:

\[L\cup M\ \ \ \ \ or\ \ \ \ \ L +M \]
concatenation:

\[LM \ \ \ \ \ or \ \ \ \ L \cdot M \]
closure(or star, or Kleene closure)

\[L^* = \bigcup_{i\ge 0}L^i \]
- Note:
  \[\empty^* = \{\epsilon\} \]

3.2 Finite Automata and Regular Expressions

3.2.1 From DFA’s to Regular Expressions

Theorem: If $L=L(A)$ for some DFA, then there is a regular expression R such that L=L(R).
- Proof:
  Assume the Regular Expression that we construct is $R_{ij}^{(k)}$ whose language is the set of strings $w$ such that $w$ is the label of a path from state $i$ to state $j$ in A, and that path has no intermediate node whose number is greater than $k$. (no constraint that $i$ and/or $k$ be less than or equal to $k$).
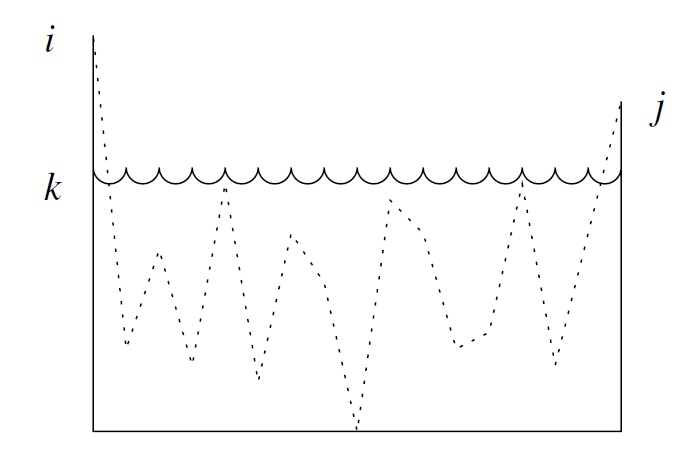
  - BASIS:
    The basis is $k=0$. Since all state are numbered 1 or above, so there is no intermediate state at all. Only 2 conditions satisfy.
    1. An arc from node i to node j.
    2. A path of length 0 that consists of only some node i.
    Then we have the following constructions:
    1. If there is no such symbol a, then $R^{(0)}_{ij}=\empty$.
    2. If there is exactly one such symbol a, then $R_{ij}^{(0)}=a$.
    3. If there are symbols $a_1,a_2,\dots,a_k$, that label arcs from state i to state j, then $R_{ij}^{(0)}=a_1+a_2+\dots+a_k$
    4. If i=j. Then we have a self-loop on i node. In the above situation, we can add label $\epsilon$ to the above Regular Expressions.
  - INDUCTION:
    Suppose there is a path from state i to state j that goes through no state higher than k There are two possible cases to consider
    1. The path does not go through state k at all:
      In this case, the label of the path is in the language of $ R^{(k-1)}_{ij} $
    2. The path goes through state k at least once:
      
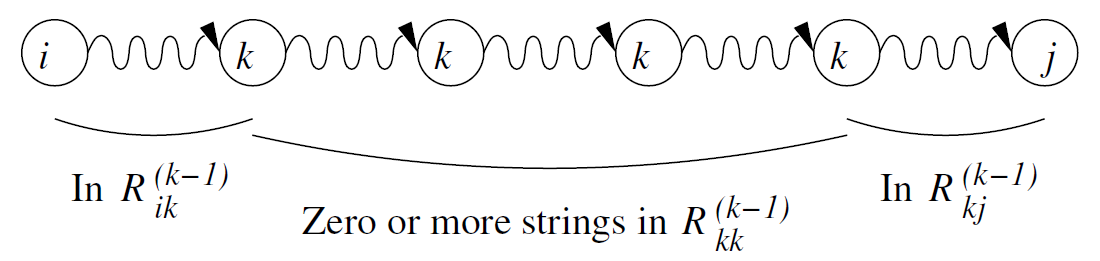      \[R_{ik}^{(k-1)}(R_{kk}^{(k-1)})^*R_{kj}^{(k-1)} \]
  - Q.E.D

3.2.2 Converting DFAs to Regular Expressions by Eliminating States

Figure:
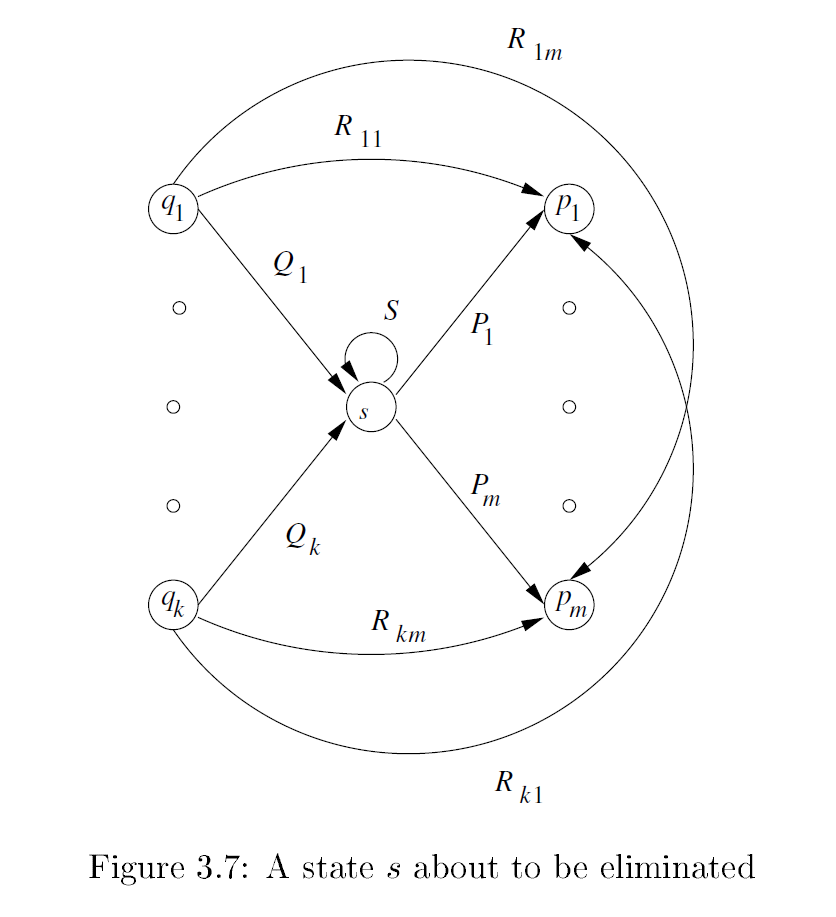
Strategy:
1. For each accepting state q, apply the above reduction process to produce an equivalent automaton with regular expression labels on the arcs.
2. If $q\ne q_0$. We have a generic two-state automaton.
  
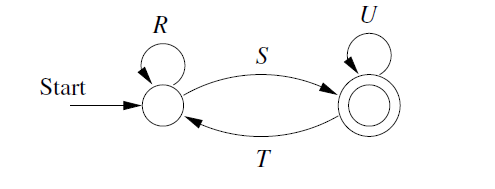
  The Regular expression is:
  
  \[(R+SU^*T)^*SU^* \]
3. If the start state is also an accepting state. We will have a one-state automaton.
  
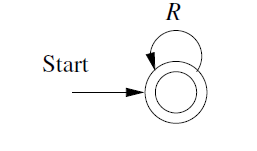
  The RE is:
  
  \[R^* \]
Example:

Key idea: Eliminating the intermediate state.

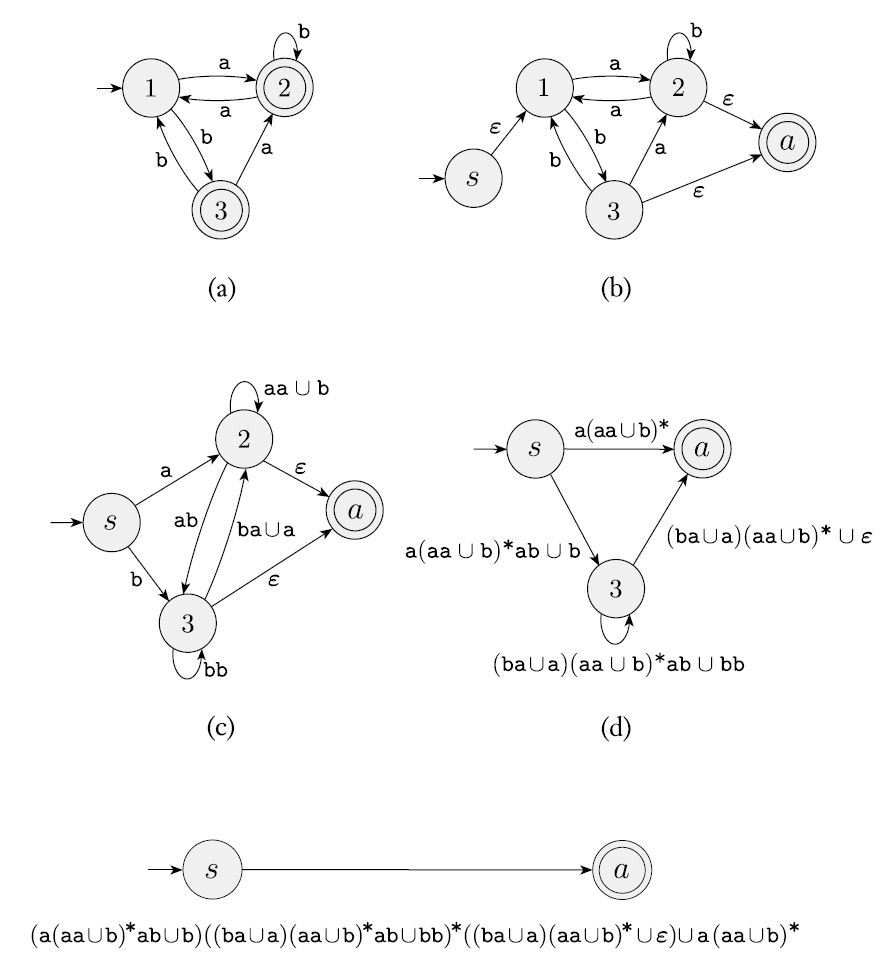
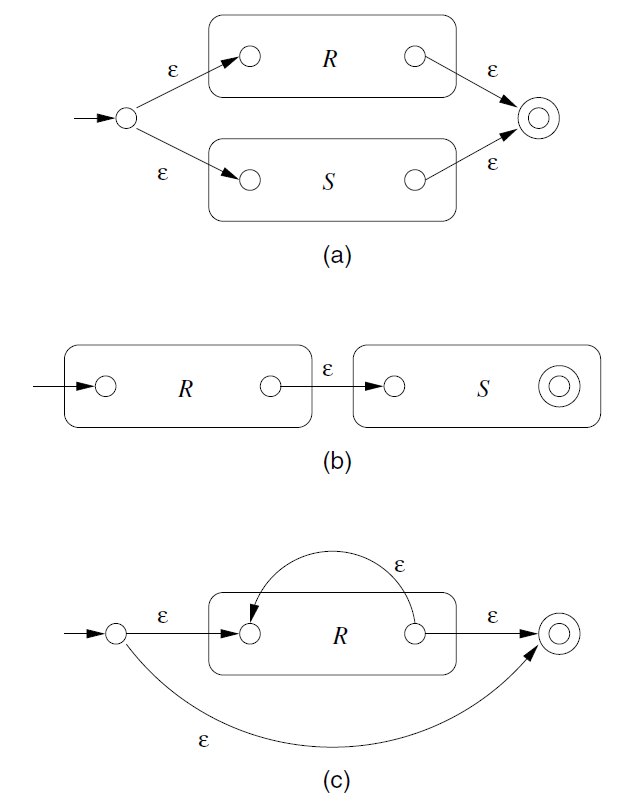
3.2.3 Converting Regular Expressions to Automata

Prove by Structural Induction on R:
- BASIS:
  1. $\{\epsilon\}$
  2. $\empty$

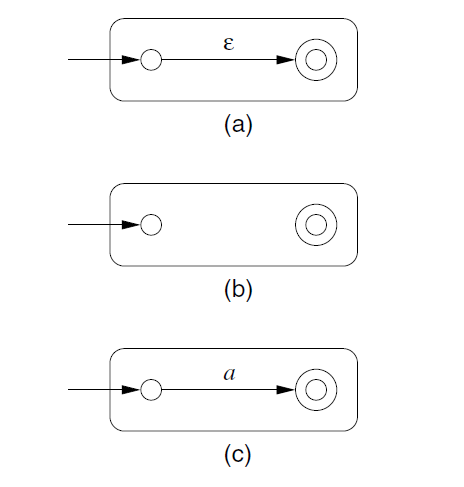
INDUCTION:
1. $R+S$.
  
  The language is $L(R)\cup L(S)$
2. $RS$
  Concatenation.
3. $R^*$
  Closure
4. $(R)$
  Unchanged.

3.4 Algebraic Laws for Regular Expressions

Simplification of RE:
1. \[\empty R = R \empty=\empty \]
  $\empty$ is an annihilator for concatenation. It results in itself when concatenated.
2. \[\empty+R = R+\empty=R \]
  $\empty$ is the identity for union. It results in the other expression whenever it appears in a union.
3. \[\epsilon L = L\epsilon = L \]
  $\epsilon$ is identity for concatenation.
4. Distributive Laws:
  
  \[L(M+N)=(M+N)L = LM+LN \]
5. The Idempotent Law:
  
  \[L+L=L \]
6. Laws Involving Closures:
  1. $(L^*)^* = L^*$
  2. $\empty^*=\epsilon$
  3. $\epsilon^*=\epsilon$
  4. $L^+=LL^*$
  5. $L^*=L^++\epsilon$
  6. $L?=\epsilon+L$
  7. $(L+M)^*=(L^*M^*)^*$
Discovering Laws for Regular Expressions:
- Theorem:
  Let E be a regular expression with variables $L_1,L_2,\dots,L_m$.
  Form concrete regular expression $C$ by replacing each occurrence of $L_i$ by the symbol $a_i$ for $i=1,2,\dots, m$
  Then for any languages $L_1,L_2,\dots,L_m$, every string $w$ in $L(E)$ can be written $w=w_1w_ 2\cdots w_k􀀀$ where each $w_i$ is in one of the languages, say $L_{j_{i}}$ and the string $a_{j_1}a_{j_2}\cdots a_{j_k}$ is in the language$ L(C)$.

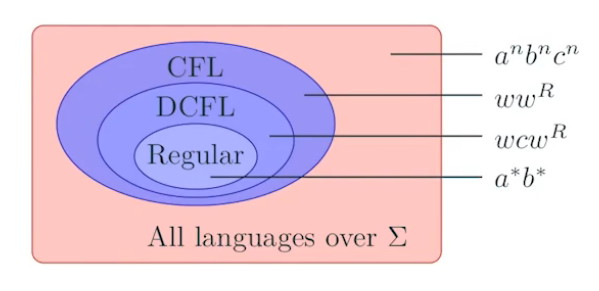
Sec4 Properties of Regular Languages

4.1 Pumping Lemma for Regular Languages

The Pumping lemma for Regular Languages:
Let $ L$ be a regular languages. Then there exists a constant $n$(which depends on $L$) such that for every string $w$ in $L$ such that $|w|\ge n$, we can break $w$ into three strings $w=xyz$, such that:
1. $y\ne \epsilon$
2. $|xy|\le n$
3. For all $k\ge 0$, the string $xy^kz$ is also in $L$.
Proof:
Using Pigeonhole Principle. Then deduct a contradiction.

4.2 Closure Properties of Regular Languages

Summary of the principal closure properties for regular languages:
Two Languages:
1. Union
2. Intersection
3. Complement
4. Difference
5. Reversal
6. Closure(star)
7. Concatenation
8. Homomorphism(substitution of strings for symbols)
9. Inverse Homomorphism

4.2.1 Closure of Regular Languages Under Boolean Operations

Closure Under Union
- Proof:
  Suppose $L = L(R), M=L(S)$
  Then: $L\cup M=L(R+S)$
Closure Under Complementation
- Find a regular expression for its complement as follows
  1. Convert the regular expression to an $\epsilon-NFA$
  2. Convert that $\epsilon- NFA$ to a $DFA$ by the subset construction
  3. Complement the accepting states of that $DFA$
  4. Turn the complement $DFA$ back into a regular expression.
- Proof:
  Let $L=L(A)$ for some $DFA\ A=(Q,\Sigma,\delta,q_0,F)$. Then $\bar{L} = L(B)$. .Then the accepting states of $A$ have become nonaccepting states of $B$, and vice versa. Then $w$ is in $L(B)$ if and only if $\hat{\delta}(q_0,w)$ is in $Q-F$, which occurs if and only if $w$ is not in $L(A)$.
Closure Under Intersection
- Prove 1:
  
  \[L\cap M = \overline{\overline{L}\cup\overline{M}} \]
- Prove 2:
  Product Construction:
  - Formal:
    \[A = (Q_L\times Q_M,\Sigma,\delta,(q_L,q_M),F_L\times F_M) \]
    where $\delta((p,q),a)=(\delta_L(p,a),\delta_M(q,a))$
Closure Under Difference:
- Prove:
  \[L-M=L\cap \overline{M} \]

4.2.2 Reversal

Construction:
1. Reverse all the arcs in the transition diagram for A
2. Make the start state of A be the only accepting state for the new automaton
3. Create a new start state $p_0$ with transitions on $\epsilon$ to all the accepting states of A
Proof:
- BASIS:
  If E is $\epsilon, \empty$ or some symbol $a$. Then the reversal of it is itself.
- INDUCTION:
  1. $E=E_1+E_2 \Rightarrow E^R=E_1^R+E_2^R$
  2. $E=E_1E_2\Rightarrow E^R=E_2^RE_1^R$
  3. $E=E_1^*\Rightarrow E^R=(E_1^R)^*$

4.2.3 Homomorphisms

A string homomorphism is a function on strings that works by substituting a particular string for each symbol

Proof:
Key idea: Prove $h(L(E))=L(h(E))$
- BASIS:
  If $\epsilon,\empty$ or $a$. Obviously
- INDUCTION:
  1. Union:
    Suppose $E=F+G$. Then $h(E)=h(F)+h(G)$.
    Then， $L(h(E))=L(h(F))\cup L(h(G))$.
    
    By inductive hypothesis, $h(L(E)) = h(L(F))\cup h(L(G)) = L(h(E))$
  2. Concatenation
  3. Closure

4.2.4 Inverse Homomorphisms

Tricks: Note that we can prove the contrapositive of the statement we set out to prove!
Theorem:
If $h$ is a homomorphism from alphabet $\Sigma$ to alphabet $T$ and $L $ is a regular language over $T$ then $h^{-1}(L)$ is also a regular language
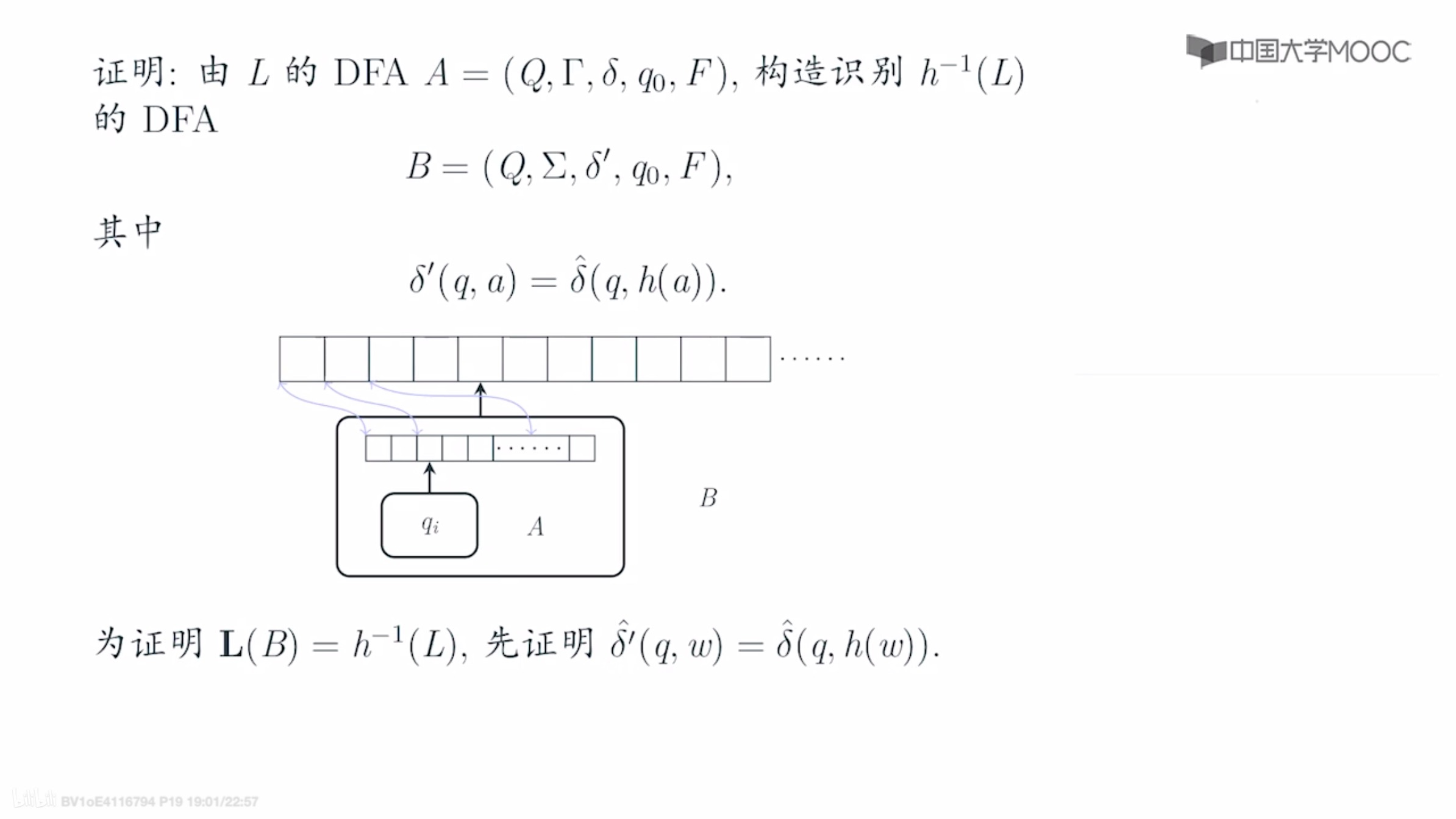
Proof:
```
核心思想：
设a是B中的输入字符
只要A接受h(a)=w，一连串后，到达A的接受状态，则B也到达接受状态
则构造性证明完毕
（B读入字符，相当于A读入一个字符串）
```
Starts with a DFA A for L:

Formally, let $L$ be $L(A)$, where $DFA\ A = (Q,T,\delta,q_0,F). $. Define a $DFA$:

\[B=(Q,\Sigma,\gamma,q_0,F) \]
where transition function $\gamma$ is constructed by the rule:

\[\gamma(q,a)=\hat{\delta}(q,h(a)) \]
(h(a) could be ε) We can easily prove that $\hat{\gamma}(q_0,w)=\hat{\delta}(q_0,h(w))$.Since the accepting states of A and B are the same, $B$ accepts $w$ if and only if $A$ accepts $h(w)$
- Mooc 证明

4.3 Decision Properties of Regular Languages

4.3.1 Converting Among Representations

Converting NFA’s to DFA’s
- Computing the closure of $\epsilon$ takes $O(n^3)$. Or $O(n^2)$
- The state of DFA can be $2^n$. After optimizing,we can reduce the time complexity to $O(n^3)$ (reachable set)
DFA-to-NFA Conversion
$O(n)$
Automaton-to-Regular-Expression Conversion
Double exponential. Because each is built from four expressions of the previous round
Regular-Expression-to-Automaton Conversion
$O(n)$

4.4 Equivalence and Minimization of Automata

4.4.1 Testing Equivalence of States

State $p$ and $q$ are equivalent if :
- For all input string $w$, $\hat{\delta}(p,w)$ is an accepting state if and only if $\hat{\delta}(q,w)$ is an accepting state.
State $p$ and $q$ are not equivalent, we say they are distinguishable. That is:
- state $p$ is distinguishable from state $q$ if there is at least one string $w$ such that one of $\hat{\delta}(p,w)$ and $\hat{\delta}(q,w)$ is accepting, and the other is not accepting.
Table-Filling Algorithm
- BASIS:
  
  If $p$ is an accepting state and $q$ is nonaccepting, then the pair $\{p,q\}$ is distinguishable
- INDUCTION:
  Let $p$ and $q$ be states such that for some input symbol $a,r=\delta(p,a)$ and $s=\delta(q,a)$ are a pair of states known to be distinguishable

4.4.3 DFA Minimization

First, eliminate any state that cannot be reached from the start state
Then, partition the remaining states into blocks, so that all states in the same block are equivalent, and no pair of states from different blocks are equivalent

Sec5 Context-Free Grammar and Context-Free Languages

Sec6 Pushdown Automata

6.3 Equivalence of PDA’s and CFG’s

6.3.1 From Grammars to Pushdown Automata

Idea:
To have the PDA simulate the sequence of left sentential forms that the grammar uses to generate a given terminal string $w$
Formal Description:
Let $G=(V,T,Q,S)$ be a CFG, construct the PDA P that accepts L(G) by empty stack as follows.

\[P=(\{q\},T,V\cup T,\delta,q,S) \]
where transition function $\delta$ is defined by:
1. For each variable A:
  
  \[\delta(q,\epsilon,A) = \{(q,\beta)|A\rightarrow\beta\ is\ a\ production\ of\ G\} \]
2. For each terminal $a, \delta(q,a,a)=\{(q,\epsilon)\}$
We can easily prove the construction by using Chomsky Normal Form

6.3.2 From PDA’s to Grammars

Idea:
Construction of an equivalent grammar uses variables each of which represents an event consisting of:
1. The net popping of some symbol X from the stack $X$, and
2. A change in state from some $p$ at the beginning to $q$ when $X $ has finally been replaced by $\epsilon$ on the stack.
We represent such a variable by the composite symbol $[pXq]$
Theorem:
Let $P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0)$ be a PDA Then there is a context free grammar $G$ such that $L(G)= N(P)$
Proof:
- Construction of $G=(V,\Sigma,R,S)$
  - Where the set of variables V consists of:
    1. The special symbol $S$ which is the start symbol, and
    2. All symbols of the form $[pXq]$ where $p$ and $q$ are states in $Q$, and $X$ is a stack symbol, in $\Gamma$
  - The productions of $G$ are as follows:
    1. For all states $p, G$ has the production $S \rightarrow [q_0Z_0p]$
    2. Let $\delta(q,a,X)$ contain the pair $(r,Y_1,Y_2,\dots,Y_k)$, where
      1. $a$ is either a symbol in $\Sigma$ or $a=\epsilon$
      2. $k$ can be any number, including 0, in which case the pair is $(r,\epsilon)$
      Then for any lists of states $r_1,r_2,\dots,r_k, G$ has the production:
      
      \[[qXr_k]\rightarrow a[rY_1r_1][r_1Y_2r_2]\dots[r_{k-1}Y_kr_k] \]
- We can prove the correctness by INDUCTION.
  
  \[[qXp]\Rightarrow^*w, if\ and\ only\ if\ (q,w,X)\vdash^*(p,\epsilon,\epsilon) \]
```
思想：
为了在栈中完整的弹出一个栈符号，需要从输入带上，消耗掉一部分输出串。
那么，消耗掉的这部分输入串，与栈中弹出的栈符号，是一种对应关系。
如果我们将栈中的栈符号，看成是一个变元，
那么就相当于，从这个栈符号的变元，可以派生出被消耗掉的那部分输出串
步骤如下:
0. 先对开始符号定义产生式，到所有的状态，模拟空栈接受PDA
1. 从栈符号X替换为Y1...Yn, 状态从q变成p(中间的转台为r1,...,rn)
2. 我们将这动作看成，先派生出一个a，然后让[pY1r1][r1Y2r2]...[rn-1Ynrn]分别派生剩下的PDA的输入串
3. 然后我们可以用归纳，就能证明充分必要性
注意，需要构造Q的n次方个产生式
```

6.4 Deterministic Pushdown Automata

6.4.1 Definition of a Deterministic PDA

We define a $PDA\ P=(Q,\Sigma,\Gamma,\delta,q_0,Z_0,F)$ to be a deterministic (DPDA), if and only if the following conditions are met:
1. $\delta(q,a,X)$ has at most one member for any $q$ in $Q$, $a$ in $\Sigma$ or $a=\epsilon$, and $X$ in $\Gamma$
2. If $\delta(q,a,X)$ is nonempty, for some a in $\Sigma$, then $\delta(q,\epsilon,X)$ must be empty

6.4.2,3 Regular Languages, CFG, and DPDA

6.4.4 DPDA’s and Ambiguous Grammars

Theorem:
If $L=N(P)$ for some DPDA P, then L has an unambiguous context-free grammar

Sec7 Properties of Context-Free Languages

7.1 Normal Forms for Context-Free Grammars

Preliminary Simplifications:
1. Eliminate Useless Symbols
2. $\epsilon-productions$
3. Eliminate unit productions

7.1.1 Eliminating Useless Symbols

Identifying the 2 things a symbol has to be able to do:
1. We say $X$ is generating if $X\Rightarrow^*w$ for some terminal string $w$. Every terminal is generating.
2. We say $X$ is reachable if there is a derivation $S\Rightarrow^*\alpha X\beta$ for some $\alpha$ and $\beta$
Order:
1. First we check Generating.
2. Then we check Reachable.

7.1.3 Eliminating ε-Productions

Nullable:
A variable A is nullable if $A\Rightarrow^*\epsilon$.
Method:
If A is nullable, then whenever A appears in a production body, say $B\rightarrow CAD$, A might derive ε. We make 2 versions of the production:
1. Without A in the body, say $B\rightarrow CD$.
2. Cannot allow A to derive ε. Say $B\rightarrow C\hat{A}D$. and $\hat{A}$s are the productions of $A\rightarrow \hat A$
Steps:
1. Find the nullable symbols
2. Consider the production R, that contains nullable symbols
3. Add the productions in R, which contains all permutation and combination of nullable symbols

7.1.4 Eliminating Unit Production

Unit production:
is a production of the form A->B, where both A and B are variables.
Find unit pair:
- BASIS: (A,A) is a unit pair for any variable A.
- INDUCTION: Suppose we have determined that (A,B) is a unit pair, and B->C is a production, where C is a variable, then (A,C) is a unit pair.
Elimination:
1. Find all the unit pairs of G
2. For each unit pair (A,B), add to $P_1$ all the productions A->α, where B->α is a non-unit production in P. Note that A=B is possible; in that way, $P_1$ contains all the non-unit productions in P

7.1.5 Chomsky Normal Form

The order of Eliminations:
1. Eliminate ε-productions
2. Eliminate unit productions
3. Eliminate useless symbols
Definition of Chomsky Normal Form:

The CFL without ε has a grammar G in which all productions are in one of 2 simple form, either:
1. A->BC
2. A->a, where a is a terminal.
Construction:
1. Arrange that all bodies of length or more consist only of variables
2. Break bodies of length, or more into a cascade of productions, each with a body consisting of two variables

7.2 The Pumping Lemma for Context-Free Languages

The Advantage of Using CNF: Turn parse trees into binary trees.

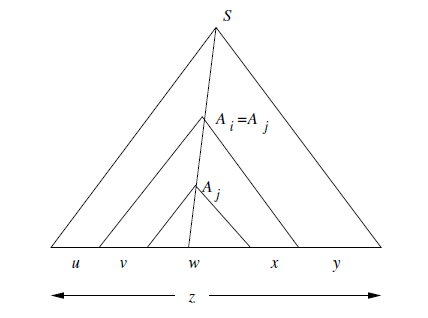
7.2.2 Statement of the Pumping Lemma

Lemma:

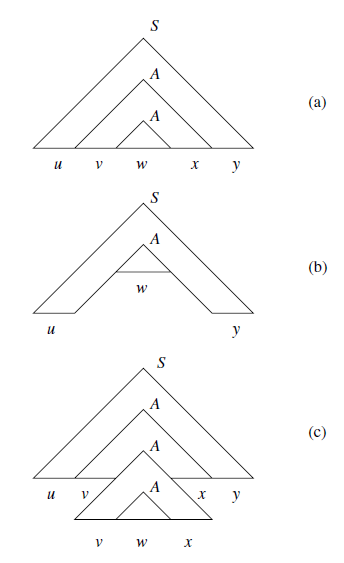
Let L be a CFL. Then there exists a constant n such that if z is any string in L such that |z| is at least n, then we can write z=uvwxy, subject to the following conditions:
1. |vwx|<=n. That is, the middle portion is not too long.
2. vx!=ε. Since v and x are the pieces to be “pumped”. This condition says that at least one of the strings we pump must not be empty.
3. For all i >= 0. $uv^iwx^iy$ is in L.
Proof of CFG-Pumping Lemma:
Using pigeonhole principle:

7.3 Closure Properties of Context-Free Languages

7.3.1 Substitutions

Theorem:
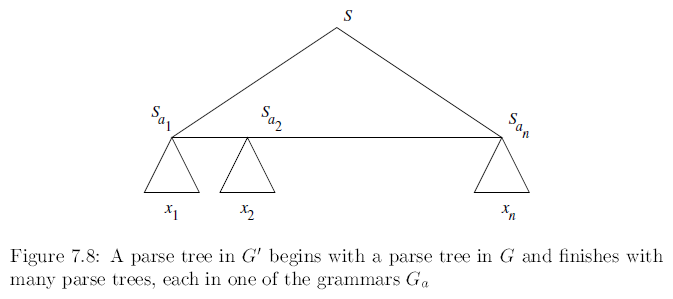
If $L$ is a context free language over alphabet $\Sigma$, and $s$ is a substitution on $\Sigma$ such that s(a) is a CFL for each a in $\Sigma$, then s(L) is a CFL
Proof:
Say G=($V,\Sigma,P,S$) for L and $G_a=(V_a,T_a,P_a,S_a)$ for each a in $\Sigma$

We construct a new grammar G’=(V’,T’,P’,S) for s(L), as follows
- V’ is the union of V and all the $V_a's$ for a in $\Sigma$
  
  \[V'=V\cup (\bigcup_{a\in T}V_a) \]
- T’ is the union of all the $T_a's$ for a in $\Sigma$
  
  \[T'=\bigcup_{a\in T}T_a \]
- P’ consists of:
  1. All productions in any $P_a$, for a in $\Sigma$
  2. The productions of P,but with each terminal a in their bodies replaced by $S_a$ everywhere a occurs

7.3.2 Applications of the Substitution Theorem

Theorem:
The context free languages are closed under the following operations
1. Union
2. Concatenation
3. Closure(*), or positive closure
4. Homomorphism
  s(a) = {h(a)}, -> , h(L) = s(L)

7.3.3 Reversal

CFL’s are closed under reversal
Proof:
Let L=L(G) for some CFL G=(V,T,P,S). Construct $G^R=(V,T,P^R,S)$, where $P^R$ is the reverse of each production in P. That is, if A->a is a production of G, the A->$a^R$ is a production of $G^R$.

7.3.4 Intersection

The CFLs are not closed under 2 CFG’s intersection.
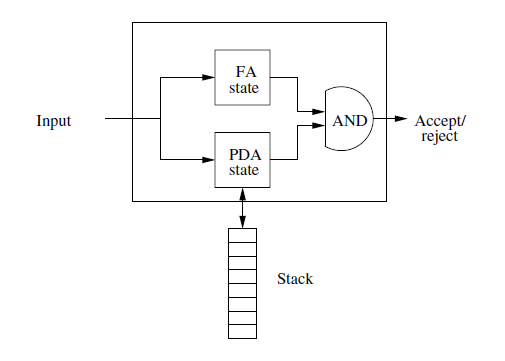
Theorem:
If L is a CFL and R is a regular language, then $L\cap R$ is a CFL.
Proof:
- Formally:
  Let
  
  \[P=(Q_P,\Sigma,\Gamma,\delta_P,q_P,Z_0,F_P) \]
  be a PDA that accepts L by final state, and let:
  
  \[A=(Q_A,\Sigma,\delta_A,q_A,F_A) \]
  ne a DFA for R. Construct PDA:
  
  \[P'=(Q_P\times Q_A, \Sigma,\Gamma,\delta,(q_P,q_A),F_P\times F_A) \]
  where $\delta((q,p),a,X)$ is defined to be the set of all pairs $((r,s),\gamma)$ such that:
  1. $s=\hat{\delta}_A(p,a)$, and
  2. Pair $(r,\gamma)$ is in $\delta_P(q,a,X)$
Another Theorems:

If we have CFL L, L1 and L2, and regular languages R:
1. L-R is CFL:
  - Proof:
    \[L-R=L\cap\bar{R} \]
2. $\bar{L}$ is not necessarily a CFL:
  - Proof:
    Because $\bar{L}$ is also Context-Free. And we have:
    \[L_1\cap L_2 =\overline{\overline{L_1}\cup\overline{L_2}} \]
    So intersection is closed, too. We have a Contradiction.
3. L1-L2 is not necessarily Context-Free
  If we choose L1 to be $\Sigma^*$. Then L1-L2 is $\overline{L2}$

7.3.5 Inverse Homomorphism

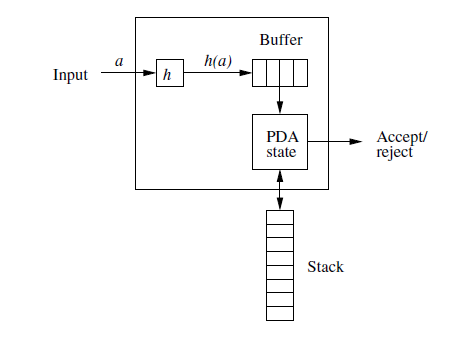
Theorem:
If L is CFL on $\Delta$, h is homomorphism from $\Sigma$ to $\Delta^*$. Then, $h^{-1}(L)$ is CFL, too.
- Proof：
  Let $PDA\ P=(Q,\Delta,\Gamma,\delta,q_0,Z_0,F)$， $L(P)=L$. Constructing PDA of $L(P')=h^{-1}(L)$ :
  
  \[P'=(Q',\Sigma,\Gamma,\delta',[q_0,\bar\epsilon],Z_0,F\times \{\bar{\epsilon}\}) \]
  In the states of P’, we use buffer, temporarily save the homomorphism string h(a) of symbol $a\in \Sigma$.
  1. $Q'\subset Q\times \Delta^*$: $\bar x$ in state $[q,\bar x]$ is buffer:
  2. Let $q\in Q$, then we define $\delta'$:
    1. $\forall [q,\bar\epsilon]\in Q\times \{\bar\epsilon\},\forall a\in \Sigma, \forall X\in \Gamma$:
      
      \[\delta'([q,\bar\epsilon],a,X)=\{([q,h(a)],X)\} \]
    2. If $\delta(q,\bar a, X)=\{(p_1,\beta_1),(p_2,\beta_2),\dots,(p_k,\beta_k)\}$, then:
      
      \[\delta'([q,\overline{ax}],\epsilon,X)=\{([p_1,\bar x],\beta_1),([p_2,\bar x],\beta_),\dots,([p_k,\bar x],\beta_k)\} \]
      Where $\bar a\in \Delta \cup\{\bar \epsilon\}$, $\bar x$ is the suffix of some h(a)

posted @ 2022-12-21 11:56 M1kanN 阅读(88) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

M1kanN's Blog

Carpe Diem and Be Patient