求最短路

目录

• 朴素Dijkstra
• 堆优化版的Dijkstra
• Bellman-Ford
• SPFA
• SPFA求负环
• Floyd

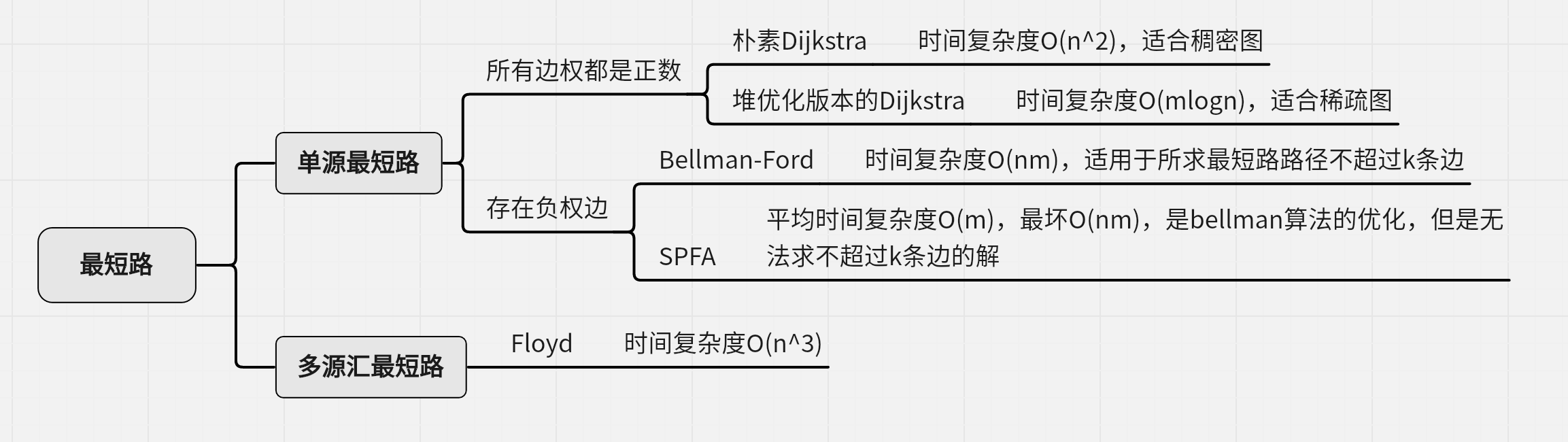
在图论中，求最短路是常见问题，往往求最短路问题存在很多限制，这使得我们需要根据限制在算法上找到最优解，因此不同的最短路算法用于求不同问题。

源指起点，汇指终点。n表示节点个数，m表示边的个数。

朴素Dijkstra

例题：https://www.acwing.com/problem/content/851/

#include <iostream>
#include <cstring>

using namespace std;

const int N = 510;

int g[N][N], dist[N];
bool st[N];

int n, m;

void dijkstra() {
    
    // 初始化dist
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for (int i = 0; i < n; i ++ ) {
        
        // 从非集合st中取出最近节点x
        int x = 0;
        for (int j = 1; j <= n; j ++ ) {
            if (!st[j] && (x == 0 || dist[x] > dist[j])) x = j;
        }
        
        // 将节点x放入集合s
        st[x] = true;
    
        // 使用节点x更新其他节点
        for (int i = 1; i <= n; i ++ ) {
            dist[i] = min(dist[i], dist[x] + g[x][i]);
        }
    }
    
    if (dist[n] == 0x3f3f3f3f) printf("-1");
    else printf("%d", dist[n]);
}

int main() {
    scanf("%d%d", &n, &m);
    
    memset(g, 0x3f, sizeof g);
    
    while (m -- ) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        
        g[a][b] = min(g[a][b], c);
    }
    
    dijkstra();
    
    return 0;
}

堆优化版的Dijkstra

例题：https://www.acwing.com/problem/content/description/852/

在朴素的dijkstra算法中，寻找非s集合中，距离1最近的点，这个过程可以使用小根堆的特性进行优化。在找离1最近的点这个过程中，无需和所有的点进行比较，因为有些点目前是无法达到的，只需要和能达到的点比较，因此heap中存放的都是1可到达的点。

#include <iostream>
#include <queue>
#include <vector>
#include <cstring>
#include <algorithm>

using namespace std;

typedef pair<int, int> PII;

const int N = 150010;

int h[N], e[N], ne[N], idx, w[N], dist[N];

bool st[N];

int n, m;

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

int dijkstra() {
    
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    // 堆中存放的都是节点1的可达节点，并且根据1到可达节点的距离进行排序
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    
    heap.push({0, 1});
    
    while (heap.size()) {
        // 在未确定距离的点集合中，找到距离1最小的点
        auto t = heap.top();
        heap.pop();
        
        int v = t.second, d = t.first;
        
        // 去重优化。由于点与点存在多条边，那么在heap中会存在距离不同但是点相同的重复数据，
        // 由于heap已经按距离进行了排序，因此距离较大的点无需再用来更新其他点距离
        if (st[v]) continue;
        st[v] = true;
        
        for (int i = h[v]; i != -1; i = ne[i]) {
            int j = e[i];
            
            // d是1到v的距离，w[i]是v到j的距离，dist[j]是1到j的距离
            if (dist[j] > d + w[i]) {
                dist[j] = d + w[i];
                heap.push({dist[j], j});
            }
        }
    }
    
    if (dist[n] == 0x3f3f3f3f) return -1;
    else return dist[n];
}

int main() {
    
    scanf("%d%d", &n, &m);
    
    memset(h, -1, sizeof h);
    
    while (m -- ) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        
        add(a, b, c);
    }
    
    printf("%d\n", dijkstra());
    
    return 0;
}

该算法会遍历到所有点的的边，并且由于进行了去重，重复点只会遍历一次，因为外层for循环是O(m)的时间，内层heap push是O(logn)的时间，总体上是mlogn。
当n=m^2 时（稀疏图），mlogn=2m^2 ，时间复杂度为O(m^2 )，会比朴素算法的O(n^2 )快很多。

总体来看，Dijkstra本质就是用一个已经确定为最短路径的点，去更新其他点到源的距离。
dijkstra不能解决负权边问题，由于我们必须确定一个已知的对短路径，因此当图中出现负权边时，会导致我们选择的最短路径在之后的更新中变得更短，如下图：

Bellman-Ford

bellman算法的思想核心也和Dijkstra一样，使用一个点更新其他点到源的距离，即所谓的松弛操作，dist[b] = min(dist[b], dist[a] + w);
只不过bellman类似于暴力的解法，循环n次，每次循环中遍历所有的边，并进行松弛操作。外层n次循环是有实际意义的，循环k次表明从源到某节点的最短距离经过的边数不超过k条。 因此bellman算法可以专门针对对路径边数有限制的题目。

例题：https://www.acwing.com/problem/content/855/

#include <iostream>
#include <cstring>

using namespace std;

const int N = 510, M = 10010;

// 存储边，a为起点，b为终点，w为权重
struct Edge {
    int a, b, w;
} Edge[M];

int dist[N], backup[N], n, m, k;

void bellman_ford() {
    
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    for (int i = 0; i < k; i ++ ) {
        
        // 将dist进行备份，备份的原因是在松弛操作中可能会导致dist[i]被覆盖
        memcpy(backup, dist, sizeof dist);
        
        for (int i = 0; i < m; i ++ ) {
            int a = Edge[i].a, b = Edge[i].b, w = Edge[i].w;
            dist[b] = min(dist[b], backup[a] + w); // 松弛操作
        }
    }

    // 松弛操作中，可能会对权重为0x3f的边削减一部分值，因此不能认为不可到达的距离一定是0x3f
    if (dist[n] > 0x3f3f3f3f / 2) printf("impossible");
    else printf("%d", dist[n]);
}

int main() {
    
    scanf("%d%d%d", &n, &m, &k);
    
    for (int i = 0; i < m; i ++ ) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        
        Edge[i] = {a, b, w};
    }
    
    bellman_ford();
    
    return 0;
}

针对注释做进一步解释：
1、memcpy(backup, dist, sizeof dist);

2、if (dist[n] > 0x3f3f3f3f / 2) printf("impossible");

bellman算法的时间复杂度为O(mn)。另外，bellman算法可以应对负权环（当图中出现一个环，并且环上的权重和为负数，就称之为负权环）在求最短路问题中，在负权环后边的点的距离将被视为无穷小，因为我们可以一直循环负权环让距离减小。bellman算法可以通过限制经过的边数，保证不陷于循环在负权环中。

SPFA

spfs算法是bellman算法的优化。在bellman算法中，暴力的将所有的边都进行松弛，但是有的点已经确定了最小距离，不在需要进行松弛。spfa就是针对该公式进行了优化dist[b] = min(dist[b], backup[a] + w);，只有dist[b]变小，对b周围的节点的更新才有意义。这和堆优化的Dijkstra有相似之处，只不过不需要挑出最小距离。

spfa算法不能处理存在负环的情况，且时间复杂度不够稳定，最坏为O(nm)。但是在99%的情况下，spfa都可以解决最短路问题，如果被卡，就需要换用上面其他算法。

例题：https://www.acwing.com/problem/content/description/853/

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

const int N = 100010;

int n, m;

int h[N], e[N], ne[N], w[N], idx;

int dist[N], st[N]; // st数组记录节点是否已经存在于队列中

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

void spfa() {
    
    // 初始化
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    queue<int> q;
    q.push(1);
    st[1] = true;
    
    while (q.size()) {
        
        int t = q.front();
        q.pop();
        st[t] = false;
        
        // 将可更新且不存在于队列中的点入队
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                
                if (!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    
    if (dist[n] == 0x3f3f3f3f) printf("impossible");
    else printf("%d", dist[n]);
}

int main() {
    
    scanf("%d%d", &n, &m);
    
    memset(h, -1, sizeof h);
    
    while (m -- ) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        
        add(a, b, w);
    }
    
    spfa();
    
    return 0;
}

SPFA求负环

spfa算法在求最短路的基础上，可以增加一些字段来记录源到其他节点经过的边数。由于spfa求最短路会因为负环的存在，而一直循环于负环中（路径越来越长，但是距离越来越短），因此我们可以同时记录经过的边数，当边数大于等于节点个数，则可认为存在负环。

例题：https://www.acwing.com/problem/content/854/

#include <iostream>
#include <cstring>
#include <queue>

using namespace std;

const int N = 2010, M = 10010;

int n, m;

int h[N], e[M], ne[M], w[M], idx;

int dist[N], st[N], cnt[N]; // cnt数组表示1到其他点的最短路径上经过的边数

void add(int a, int b, int c) {
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

bool spfa() {
    
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    
    queue<int> q;
    
    // 求整个图中的负环（而不是1-n路径上的负环）需要将所有点都作为源入队
    for (int i = 1; i <= n; i ++ ) {
        q.push(i);
        st[i] = true;
    }
    
    while (q.size()) {
        
        int t = q.front();
        q.pop();
        st[t] = false;
        
        for (int i = h[t]; i != -1; i = ne[i]) {
            int j = e[i];
            
            if (dist[j] > dist[t] + w[i]) {
                dist[j] = dist[t] + w[i];
                
                // n个节点的图中求最短路，没有负环时最多经过n-1条边，当超过n-1条边，则表示有负环
                cnt[j] = cnt[t] + 1;
                if (cnt[j] >= n) return true;
                
                if (!st[j]) {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }
    
    return false;
}

int main() {
    
    scanf("%d%d", &n, &m);
    
    memset(h, -1, sizeof h);
    
    while (m -- ) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        
        add(a, b, w);
    }
    
    if (spfa()) printf("Yes");
    else printf("No");
    
    return 0;
}

Floyd

floyd基于动态规划可求出任意源汇之间的最短距离。代码比较简单，好背。

例题：https://www.acwing.com/problem/content/856/

#include <iostream>
#include <algorithm>

using namespace std;

const int N = 210;

int d[N][N]; // d[i][j]表示节点i到节点j的最短距离

int n, m, q;

void floyd() {
    for (int k = 1; k <= n; k ++ )
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

int main() {
    
    scanf("%d%d%d", &n, &m, &q);
    
    for (int i = 0; i < N; i ++ ) {
        for (int j = 0; j < N; j ++ ) {
            if (i == j) d[i][j] = 0;
            else d[i][j] = 0x3f3f3f3f;
        }
    }
    
    while (m -- ) {
        int a, b, w;
        scanf("%d%d%d", &a, &b, &w);
        
        d[a][b] = min(d[a][b], w);
    }
    
    floyd();
    
    while (q -- ) {
        int a, b;
        scanf("%d%d", &a, &b);
        
        if (d[a][b] > 0x3f3f3f3f / 2) printf("impossible\n");
        else printf("%d\n", d[a][b]);
    }
    
    return 0;
}