矩阵快速幂

矩阵快速幂即把快速幂的乘法操作改为矩阵乘法。 一般用来快速求通项的值，难点在于写出矩阵递推式，从而用矩阵快速幂求解。 一般来说，递推式的形式是A(n) = T * A(n-1),T称为转移矩阵，要求是常数矩阵，一般是靠凑出来的。技巧是第一行一般为通项公式，然后开始凑，不想要的项就把系数设为0，直到把T凑成一个方阵。注意A(n)与A(n-1)中对应各元素下标差为1。最后可得，A(n)=T^(n-1) * A(1)，A(n)的第一个元素即为答案。 常见递推式：

f(n)=af(n-1)+bf(n-2)+c

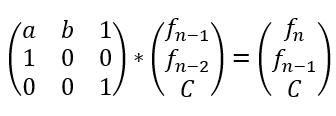
f(n)=c^n-f(n-1)

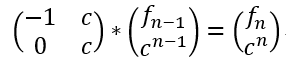
以下是矩阵快速幂的板子：

typedef long long ll;
inline ll add(ll a,ll b)
{
    a+=b;
    if (a>=mod)
        a-=mod;
    if (a<0)
        a+=mod;
    return a;
}
inline ll mul(ll a,ll b)
{
    return a*b%mod;
}
struct matrix
{
    static const int N=5;
    int mat[N][N],n,m;
    matrix(){}
    matrix(int _n,int _m,int v)
    {
        n=_n;
        m=_m;
        for (int i=0;i<n;++i)
            for (int j=0;j<m;++j)
                mat[i][j]=i==j?v:0;
    }
    matrix operator * (const matrix& a) const
    {
        matrix res(n,a.m,0);
        for (int i=0;i<n;++i)
            for (int j=0;j<a.m;++j)
                for (int k=0;k<m;++k)
                    res.mat[i][j]=add(res.mat[i][j],mul(mat[i][k],a.mat[k][j]));
        return res;
    }
    matrix operator ^ (ll b) const
    {
        matrix res(n,n,1),a=*this;
        while (b)
        {
            if (b&1)
                res=res*a;
            a=a*a;
            b>>=1;
        }
        return res;
    }
};