第二章 基于距离的分类器
预习笔记
MED分类器
- 基于欧式距离的分类器，欧式距离 \(d(x1,x2)=(x2-x1)^{T}*(x2-x1)\)
- 判别方法： \((x-μ_{1})^{T}(x-μ_{1})<(x-μ_{2})^{T}(x-μ_{2})? C1类 : C2类\)
- 受特征的量纲、分布不同的影响，易导致分类错误，一般不直接用欧式距离进行分类
MICD分类器
- 基于马氏距离的分类器，马氏距离 \(d(x1,x2)=(x2-x1)^{T}Σ_{x}^{-1}(x2-x1)\)
- 判别方法：\((x-μ_{1})^{T}Σ_{x}^{-1}(x-μ_{1})<(x-μ_{2})^{T}Σ_{x}^{-1}(x-μ_{2})?C1类：C2类\)
- 针对欧式距离出现的问题，对特征进行解耦与白化，转化后的点间距离为马氏距离
- 消除了特征间的相关性并使特征具有相同方差，从而使其不受量纲和分布的影响，提高分类准确度
- 但在距离相等时，倾向于归于方差较大的类
复习笔记
MED分类器
类的原型
用来代表这个类的一个模式或者一组量，便于计算该类和测试样本之间的距离。
均值
最近邻
几种常见的距离度量
MED分类器
- 概念:最小欧式距离分类器(Minimum Euclidean Distance Classifier)
- 距离衡量:欧式距离
- 类的原型:均值
- 决策边界: $ (x-μ_{1})^{T} (x-μ_{1}) - (x-μ_{2})^{T} (x-μ_{2}) = 0 $
- 判别公式: \((x-μ_{1})^{T}(x-μ_{1})<(x-μ_{2})^{T}(x-μ_{2})? C1类 : C2类\)
- 缺陷：易受特征量纲和分布的影响
特征白化
令W=W1W2，目标使 $ W Σ_{x} W^{T} = I $
解耦
通过W1实现协方差矩阵对角化,去除特征之间的相关性。
白化
通过W2对上一步变换后的特征再进行尺度变换,实现所有特征具有相同方差。
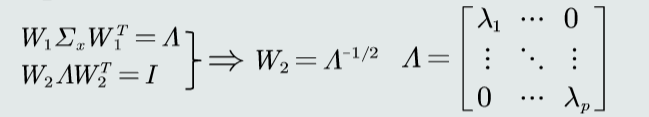
马氏距离
MICD分类器
- 最小类内距离分类器(Minimum Intra-class DistanceClassifier)，基于马氏距离的分类器。
- 距离度量:马氏距离
- 类的原型:均值
- 决策边界:\((x-μ_{1})^{T}Σ_{x}^{-1}(x-μ_{1})-(x-μ_{2})^{T}Σ_{x}^{-1}(x-μ_{2})=0\)
- 判别公式:\((x-μ_{1})^{T}Σ_{x}^{-1}(x-μ_{1})<(x-μ_{2})^{T}Σ_{x}^{-1}(x-μ_{2})?C1类：C2类\)
- 缺陷:均值相同时，会选择方差较大的类
