第一章 模式识别基本概念
预习笔记
模式识别
- 一般由特征提取、回归器两模块组成
- 大致分为回归与分类两种形式
- 对于输入的待识别模式，根据已有的知识进行判别决策，输出其回归值或所属类别
机器学习
- 通过一定量的训练样本，来学习模型的参数，有以下几类：
- 有监督式学习：训练样本给定真值
- 无监督式学习：训练样本不给真值，难度较大，用于聚类、图像分割等
- 半监督式学习：仅给定一部分训练样本的真值，用于网络流数据等
- 强化学习：真值滞后反馈，适用于需要累积多次决策才知道结果好坏的任务
复习笔记
模式识别的定义
- 模式识别：根据已有知识的表达，针对待识别模式，判别其决策所属的类别或者预测其对应的回归值
- 根据任务，可分为分类与回归两种形式
- 分类：输出量是离散的类型表达，即输出待识别模式所属的类别
- 回归：输出量是单个/多个维度的连续信号表达（回归值）
- 回归是分类的基础：离散的类别值是由回归值做判别决策得到的
模型的数学表达
- 数学解释:模式识别可以看做一种函数映射f(x),将待识别模式x从输入空间映射到输出空间。
- 函数f(x)是关于已有知识的表达。
- 函数f(x)的形式:可解析表达的、难以解析表达的。
- 函数f(x)的输出:确定值、概率值。
特征向量
残差向量
欧式距离
$ d(x,y)=(x-y)^{T} (x-y) = Σ_{j=1}^{p} (x_j-y_j)^{2} $
机器学习基本概念
模型的参数与结构
- 模型的参数：$ θ={θ_1，θ_2，…，θ_M} $
- 模型的结构：函数f的形式
线性模型
- $ y = w^Tx+w_0 $
- 其中w和 $ w_0 $为模型参数，线性模型适用于线性可分的数据
非线性模型
- y=g(x)
- 适用于线性不可分的数据，如异或问题。
- 常见模型：多项式，决策树，神经网络
样本量 vs 模型参数量
- 训练样本个数 = 模型参数个数 ：参数有唯一解
- 训练样本个数 > 模型参数个数 ：没有准确的解
- 训练样本个数 < 模型参数个数 ：无数个解/无解
目标函数
$ L=(θ|{x_i}) $
优化算法
得到模型参数的最优解$ θ^{*} = argmin_{θ} L(θ|{x_n}) $
流程示意图
学习方式
- 有监督式学习：训练样本给定真值
- 无监督式学习：训练样本不给真值，难度较大，用于聚类、图像分割等
- 半监督式学习：仅给定一部分训练样本的真值，用于网络流数据等
- 强化学习：真值滞后反馈，适用于需要累积多次决策才知道结果好坏的任务
泛化能力
- 训练集(training set): 模型训练所用的样本数据。集合中的每个样本称作训练样本。
- 测试集(test set): 测试模型性能所用的样本数据。集合中的每个样本称作测试样本。
- 训练误差(training error): 模型在训练集上的误差。
- 测试误差(test error): 模型在测试集上的误差。它反映了模型的泛化能力，也称作泛化误差。
- 泛化能力: 训练得到的模型要对新的（训练过程中未看见的）模式具有决策能力
- 过拟合: 过于拟合训练数据，因此模型训练阶段表现很好，但是在测试阶段表现很差。
评估方法
留出法
k折交叉验证
留一验证
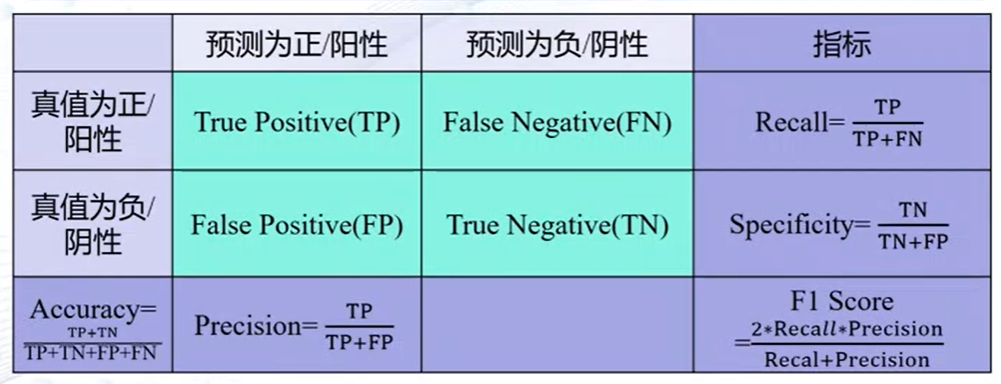
性能指标度量
- 准确度（Accuracy）
- 精度（Precision）
- 召回率（Recall）
