最远 Manhattan 距离
最远 Manhattan 距离
处理问题
K维空间下的n个点,求两点最远曼哈顿距离
思路
以二维为例介绍算法思想,即可类推到k维。对于P,Q两点,曼哈顿距离|Px-Qx|+|Py-Qy|可看作(±Px±Py)-(±Qx±Qy),不难发现Px应该与Qx的符号相同,Py与Qy符号相同,因此共四种情况。这样写的好处是,每个点可以表示成相同的形式(±Px±Py)。而曼哈顿距离一定是四种情况中值最大的那种,所以要求两点最远曼哈顿距离,可以枚举所有的取符号情况,对于每种情况,维护出上述表示下n个点的最大值与最小值,求出差值。则最远的曼哈顿距离一定是所有情况中的最大差值。
代码描述
ll max_Manhattan(ll p[][10],int n,int k)
{
ll ans=0;
for (int s=0;s<(1<<k);++s)
{
ll mx=-1e18,mn=1e18;
for (int i=0;i<n;++i)
{
ll tmp=0;
for (int j=0;j<k;++j)
tmp+=(s&(1<<j))?p[i][j]:-p[i][j];
mx=max(mx,tmp),mn=min(mn,tmp);
}
ans=max(ans,mx-mn);
}
return ans;
}
应用
一般题目可能不会太直白的要求最远曼哈顿距离,以今年多校的一道题为例,可以HDU上找到J.CSGO.
题目大意:
给n个主武器,m个副武器。每个武器有1个s属性和k个x属性。要求选取主副两把武器,使得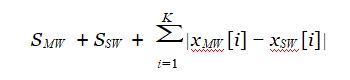 最大。
最大。
思路:
现在再来看这道题,可以发现其形式很像求K维下最远曼哈顿距离。前面多的两项可以看作第k+1维,为了保证它们的形式是两项相加,将其中一个武器集合的s属性都置为负即可。然后就做一次k维下n个点和m个点之间取两点的最远曼哈顿距离。要注意,选取的点必须分属不同集合。因此我的处理方式是,每种取符号情况下,分别维护两个武器集合的最值,求差值。(也有更巧妙的处理方法,如处理两种武器的s值,最后再修正答案,这里不赘述,可以看一下该题相关博客题解)
代码:
#include<bits/stdc++.h>
#define dd(x) cout<<#x<<" = "<<x<<" "
#define de(x) cout<<#x<<" = "<<x<<"\n"
#define sz(x) int(x.size())
#define All(x) x.begin(),x.end()
#define pb push_back
#define mp make_pair
#define fi first
#define se second
using namespace std;
typedef long long ll;
typedef long double ld;
typedef pair<int,int> P;
typedef priority_queue<int> BQ;
typedef priority_queue<int,vector<int>,greater<int> > SQ;
const int maxn=1e5+10,mod=1e9+7,INF=0x3f3f3f3f;
int a[maxn][10],b[maxn][10];
void cal(int p[][10],int n,int k,int sta,ll& mx,ll& mn)
{
mx=-1e18,mn=1e18;
for (int i=0;i<n;++i)
{
ll tmp=0;
for (int j=0;j<k;++j)
{
if (sta&(1<<j))
tmp+=p[i][j];
else
tmp-=p[i][j];
}
mx=max(mx,tmp),mn=min(mn,tmp);
}
}
ll max_Manhattan(int n,int m,int k)
{
ll ans=0,amax,amin,bmax,bmin;
for (int sta=0;sta<(1<<k);++sta)
{
cal(a,n,k,sta,amax,amin);
cal(b,m,k,sta,bmax,bmin);
ans=max(ans,max(amax-bmin,bmax-amin));
}
return ans;
}
int main()
{
int T;
cin>>T;
while (T--)
{
int n,m,k;
scanf("%d%d%d",&n,&m,&k);
for (int i=0;i<n;++i)
for (int j=0;j<=k;++j)
scanf("%d",&a[i][j]);
for (int i=0;i<m;++i)
{
for (int j=0;j<=k;++j)
scanf("%d",&b[i][j]);
b[i][0]*=-1;
}
printf("%lld\n",max_Manhattan(n,m,k+1));
}
return 0;
}
再附上一道CF上的题G. Multidimensional Queries
题目大意:给K维空间下的n个点,编号1-n。有两种操作,1重置某个编号的点的坐标,2询问某个编号区间内最远两点的曼哈顿距离。
思路:直白的求最远曼哈顿距离,不过是带有修改操作和区间询问,因此需要线段树来维护每个取符号情况下的区间最值。思想没有变化,也不需要什么技巧,不赘述。
代码:
#include<bits/stdc++.h>
#define dd(x) cout<<#x<<" = "<<x<<" "
#define de(x) cout<<#x<<" = "<<x<<endl
#define fi first
#define se second
#define mp make_pair
#define pb push_back
using namespace std;
typedef long long ll;
typedef pair<int,int> P;
typedef vector<int> V;
typedef map<int,int> M;
typedef queue<int> Q;
typedef priority_queue<int> BQ;
typedef priority_queue<int,vector<int>,greater<int> > SQ;
const int maxn=2e5+10,INF=0x3f3f3f3f;
int a[maxn][6],mx[maxn<<2][33],mn[maxn<<2][33];
int n,k;
inline void push_up(int id)
{
for (int s=0;s<(1<<k);++s)
mx[id][s]=max(mx[id<<1][s],mx[id<<1|1][s]),
mn[id][s]=min(mn[id<<1][s],mn[id<<1|1][s]);
}
void cal(int p,int id)
{
for (int s=0;s<(1<<k);++s)
{
int tmp=0;
for (int i=0;i<k;++i)
tmp+=(s&(1<<i))?a[p][i]:-a[p][i];
mx[id][s]=mn[id][s]=tmp;
}
}
void build(int l,int r,int id)
{
if (l==r)
{
cal(l,id);
return;
}
int mid=(l+r)>>1;
build(l,mid,id<<1);
build(mid+1,r,id<<1|1);
push_up(id);
}
void upd(int p,int l,int r,int id)
{
if (l==r)
{
cal(p,id);
return;
}
int mid=(l+r)>>1;
if (p<=mid)
upd(p,l,mid,id<<1);
else
upd(p,mid+1,r,id<<1|1);
push_up(id);
}
void qry(int L,int R,int& Max,int& Min,int l,int r,int id,int s)
{
if (L<=l&&r<=R)
{
Max=max(Max,mx[id][s]),Min=min(Min,mn[id][s]);
return;
}
int mid=(l+r)>>1;
if (R>mid)
qry(L,R,Max,Min,mid+1,r,id<<1|1,s);
if (L<=mid)
qry(L,R,Max,Min,l,mid,id<<1,s);
}
int query(int L,int R)
{
int ans=0;
for (int s=0;s<(1<<k);++s)
{
int Max=-INF,Min=INF;
qry(L,R,Max,Min,1,n,1,s);
ans=max(ans,Max-Min);
}
return ans;
}
int main()
{
cin>>n>>k;
for (int i=1;i<=n;++i)
for (int j=0;j<k;++j)
scanf("%d",&a[i][j]);
build(1,n,1);
int q;
cin>>q;
while (q--)
{
int op;
scanf("%d",&op);
if (op==1)
{
int id;
scanf("%d",&id);
for (int i=0;i<k;++i)
scanf("%d",&a[id][i]);
upd(id,1,n,1);
}
else
{
int l,r;
scanf("%d%d",&l,&r);
printf("%d\n",query(l,r));
}
}
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号