论文阅读笔记（五）【CVPR2012】:Large Scale Metric Learning from Equivalence Constraints

由于在读文献期间多次遇见KISSME，都引自这篇CVPR，所以详细学习一下.

Introduction

度量学习在机器学习领域有很大作用，其中一类是马氏度量学习(Mahalanobis metric learning). 什么是马氏距离？参考该篇文章【传送门】

KISS含义为：keep it simple and straightforward

 

Learning a Mahalanobis Metric

对于两个数据点 xi、xj，基于马氏距离的相似度为：

　　

如果两个数据属于同一类，记为 y_ij = 1，否则 y_ij = 0.

（1）Large Margin Nearest Neighbor Metric（LMNN）：

大间隔最近邻居(LMNN)对应的参考文献有人做了阅读梳理【传送门】

目标：使得 k 个最近邻样本总是属于同一类别，且不同类别样本之间的距离很大.

代价函数：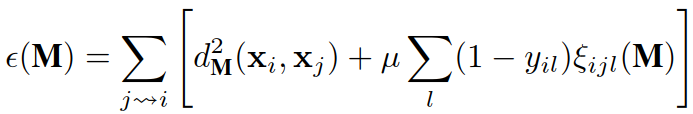

其中： 

理解：上式第一项用于惩罚与输入样本距离过大的目标邻居，第二项用于惩罚与输入样本类别不同且距离过小的样本，即侵入样本（至少保持1个单位的距离）.

通过最小化代价函数从而求解 M.

梯度下降：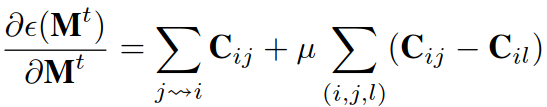

其中：

 

（2）Information Theoretic Metric Learning（ITML）：

目标：在距离函数约束下最小化两个多元高斯之间的微分相对熵的问题.（没理解）

通过使用Bregman projection的凸优化方法，求解 M.

（凸优化基础为0，没看明白）

不断更新该式子获得 M： 

 

（3）Linear Discriminant Metric Learning（LDML）：

目标：对于一对图片，判断是否是同一个对象

概率模型：

最大化的目标函数：

通过梯度下降来求解 M：

 

（4）上述三种方法特点：

① 都需要进行迭代，计算成本高；

② 相似的pairs在 C 的方向上得到优化，不相似的pairs在 C 的反方向上得到优化.

 

KISS Metric Learning

H₁：假设同一类，H₀：假设非同一类，似然比为：

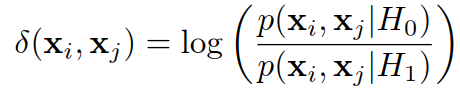
似然比较高意味着不是同一类（H₀接受），似然比较低意味着是同一类（H₀拒绝）. 

定义，变形过程如下：

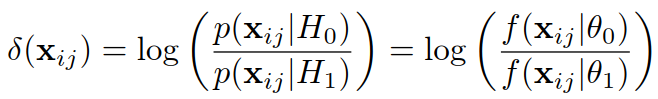
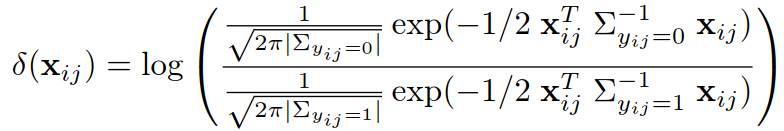
其中：

去除常数项（常数项只提供偏移offset）：

 

 由：

 得：