改善深层神经网络（二）优化算法

1、Mini-batch 梯度下降：

（1）问题背景：

假设数据集含有500万个样本，数据量庞大，训练速度缓慢.

数据构成为：

X = [x⁽¹⁾, x⁽²⁾, ..., x^(m)]   规格：n*m

Y = [y⁽¹⁾, y⁽²⁾, ..., y^(m)]   规格：1*m

若将数据集分成若干个子集，即mini-batch，每个子集仅含有1000个样本.

划分结果：X^{i}   规格：n*1000      Y^{i}   规格：1*1000

X^{1}: [x⁽¹⁾, x⁽²⁾, ..., x⁽¹⁰⁰⁰⁾]

X^{2}: [x⁽¹⁰⁰¹⁾, x⁽¹⁰⁰²⁾, ..., x⁽²⁰⁰⁰⁾]

...

X^{5000}

Y^{1}: [y⁽¹⁾, y⁽²⁾, ..., y⁽¹⁰⁰⁰⁾]

Y^{2}: [y⁽¹⁰⁰¹⁾, y⁽¹⁰⁰²⁾, ..., y⁽²⁰⁰⁰⁾]

...

Y^{5000}

 

（2）算法流程：

Forward prop on X^{t}:

　　Z^[1] = W^[1]X^{t} + b^[1]

　　A^[1] = g^[1](Z^[1])

　　...

　　A^[L] = g^[L](Z^[L])

Compute cost J^{t} ：

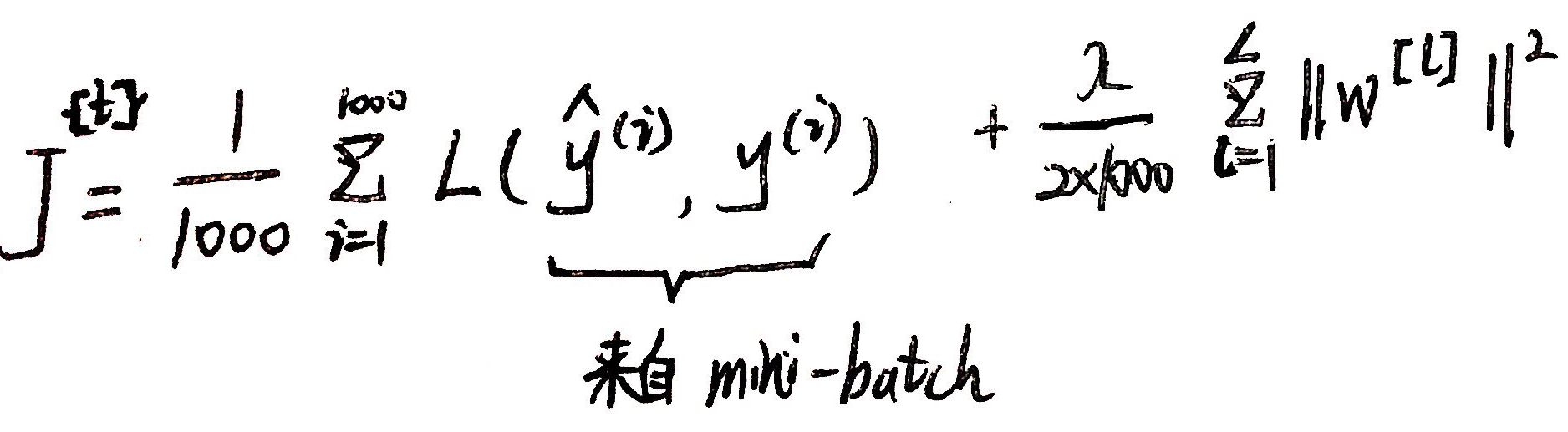
Backprop to compute gradient with J^{t} using (X^{t}, Y^{t}):

W^[l] = W^[l] - α * dW^[l]

b^[l] = b^[l] - α * db^[l]

以上对一个mini-batch进行一次梯度下降，每次repeat都对5000个mini-batch进行一次梯度下降.

 

（3）梯度下降过程：

由于mini-batch一次只操作小部分的数据集，仅仅一次的梯度下降不一定对整体产生更好的效果，因此会出现噪声.

 

（4）设置mini-batch的大小：

当size = m，即等同于批量梯度下降；（蓝色线条）

当size = 1，即等同于随机梯度下降.（紫色线条）

两种极端条件下的下降过程：

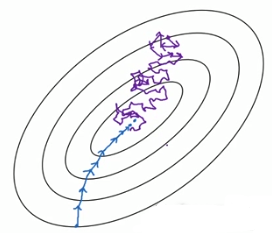
如何选择size？

如果数据集较小（<2000），直接使用batch梯度下降；

如果数据集较大，一般的mini-batch大小为64-512.

 

2、指数加权平均：

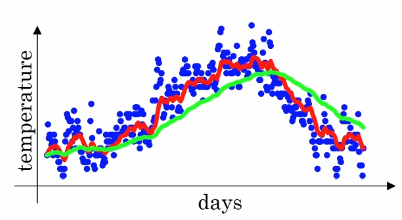
（1）举例：气温变化数据的拟合

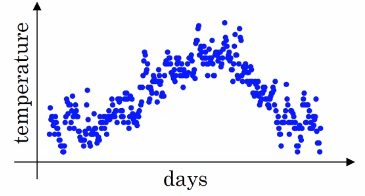
 V_t = βV_t-1 + (1-β)θ_t

作用效果：V_t ≈ 1/(1-β) 天的平均温度.

若 β = 0.9，V_t ≈ 10天的平均气温；(红色）

若 β = 0.98，V_t ≈ 50天的平均气温；(绿色)

若 β = 0.5，V_t ≈ 2天的平均气温.(黄色)

 

（2）原理：

 

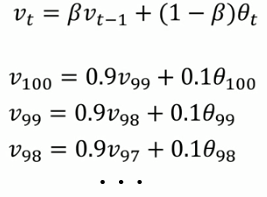
 展开式：

V₁₀₀ = 0.1 θ₁₀₀ + 0.9 V₉₉

　　  = 0.1 θ₁₀₀ + 0.9(0.1 θ₉₉ + 0.9 V₉₉) = 0.1 θ₁₀₀ + 0.9*0.1 θ₉₉ + 0.9² V₉₉

　　  = ... ...

　　  = 0.1 θ₁₀₀ + 0.1*0.9 θ₉₉ + 0.1*0.9² θ₉₈ + 0.1*0.9³ θ₉₇ + 0.1*0.9⁴ θ₉₆ + ... + 0.1*0.9⁹⁹ θ₁ + 0.9¹⁰⁰ V₁  

可以看出，当10次时 0.9¹⁰ ≈ 0.35 ≈ 1/e，之后的项系数较小，即权重下降为不到当日权重的三分之一，可以视为前10项的平均值.

当 β = 0.98时，0.98⁵⁰≈ 1/e.

为什么不直接使用前若干项的值求avg呢？因为存在大数据量的情况，无法一次性读取大量数据，指数加权平均可以仅从1项开始计算.

 

（3）Bias correction（偏差修正）

当计算移动平均数时，初始化 V₀ = 0，V₁ = 0.98 * V₀ + 0.02 θ₁ = 0.02 θ₁.

因此数据的前几项会比较小，不符合预测结果.

使用 V_t = V_t / (1 - β^t) 消除偏差：

当 t 较小时，如 t = 2，V_t = V_t / (1 - 0.98²) = V_t / 0.0396 修正了偏差.

当 t 较大时，如 t = 100，除数接近于1，不需要修真偏差.

 

 3、Gradient descent with momentum（动量梯度下降法）：

（1）问题背景：

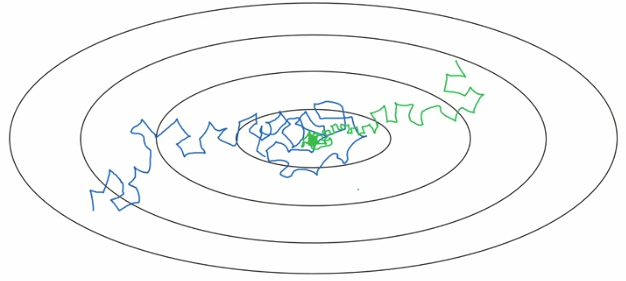
当使用梯度下降时，出现下图的情况：

期望的下降过程是：纵向跨度小一点，横向跨度大一点

 

（2）算法流程：

On iteration t：

　　Compute dW, db on current mini-batch　

　　V_dW = β V_dW + (1 - β) dW

　　V_db = β V_db + (1 - β) db

　　W = W - α V_dW

　　b = b - α V_db

如果上下波动很大，那么在使用指数加权平均时候会抵消正负的波动.

如果横向的V_dW很大，平均值也大，会依然保持较大的跨度.

注：有些情况将公式中的 (1 - β) 删除了，效果类似. 通常设置 β = 0.9 .

 

4、RMSprop（Root mean square prop 加速梯度下降）算法：

解决的问题同上

（1）算法流程：

On iteration t：

　　Compute dW, db on current mini-batch　

　　S_dW = β S_dW + (1 - β) dW²

　　S_db = β S_db + (1 - β) db²

　　W = W - α dW / √ (S_dW + ε）

　　b = b - α db / √ (S_db + ε)

注：加上 ε 是为了避免除数趋向于0.

 

（2）原理：

假设纵向是 b，横向是 W.

当上下跨幅较大，左右跨幅较小时，dW较小，db 较大. 由此会使得 S_dW 较小，S_db 较大. 进而使得 dW / √ S_dW 更大，db / √ S_db 更小

 

5、Adam（Adaptive moment estimation）算法：

结合了 momentum 和 RMSprop

（1）算法流程：

V_dW = 0, S_dW = 0, V_db = 0, S_db = 0

On iteration t：

　　Compute dW, db on current mini-batch　

　　V_dW = β₁ V_dW + (1 - β₁) dW

　　V_db = β₁ V_db + (1 - β₁) db

　　S_dW = β₂ S_dW + (1 - β₂) dW²

　　S_db = β₂ S_db + (1 - β₂) db²

　　V_dW^corrected = V_dW / (1 - β₁^t)

　　V_db^corrected = V_db / (1 - β₁^t)

　　S_dW^corrected = S_dW / (1 - β₂^t)

　　S_db^corrected = S_db / (1 - β₂^t)

　　W = W - α V_dW^corrected / √ (SdW^corrected + ε）

　　b = b - α Vdb^corrected / √ (S_db^corrected + ε)

 

（2）参数设置：

α：正数

β₁：0.9（推荐）

β₂：0.999（推荐）

ε：10^-8（推荐）

 

6、学习率衰减：

（1）问题背景：

使用mini-batch梯度下降时，由于 α 是个固定值，下降到接近最优解时，会在解的附近徘徊. 

若将 α 不断减小，跨度也不断减小，最后也可能只是不断接近解，但不能到达.

 

（2）解决方法：

1 epoch = 1 pass through data

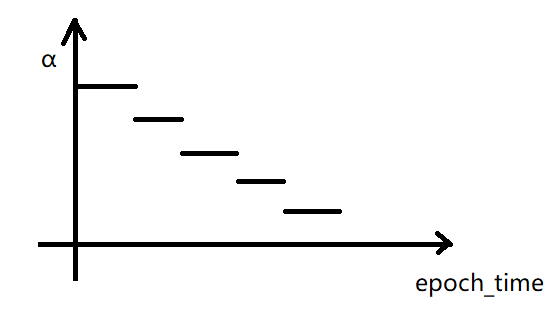
① α = 1 / (1 + decay_rate * epoch_time)

其中 decay rate 为衰减率.

② α = α₀ * 0.95^epoch_time （指数衰减）

③ α = α₀ * k / √epoch_time

④ 离散下降：