改善深层神经网络（一）深度学习的实用层面

1、L 层神经网络正则化：

（1）L2 正则化：

 

（2）为什么正则化可以避免过拟合？

 当 lambda 足够大时，最小化 J 时，就会使得权重矩阵 w 趋近于0，神经网络简化为高偏差状态：

 lambda 较大，w 较小，由 z = w * a + b，z 也较小，以 tanh 函数为例：

当 z 在较小的阶段，函数 g(z) 趋近于线性. 如果每一层都趋近线性，该网络为线性网络，不会产生过拟合的情况.

 

（3）dropout正则化（随机失活）：

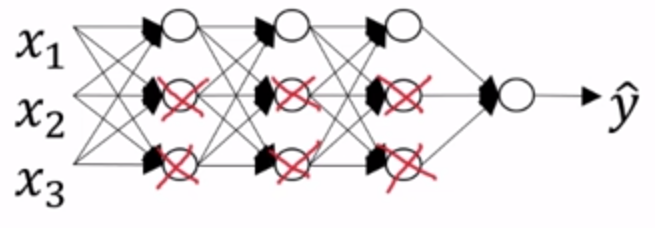
 神经网络的每一个节点都含有 p 的概率失活，如下图：

 

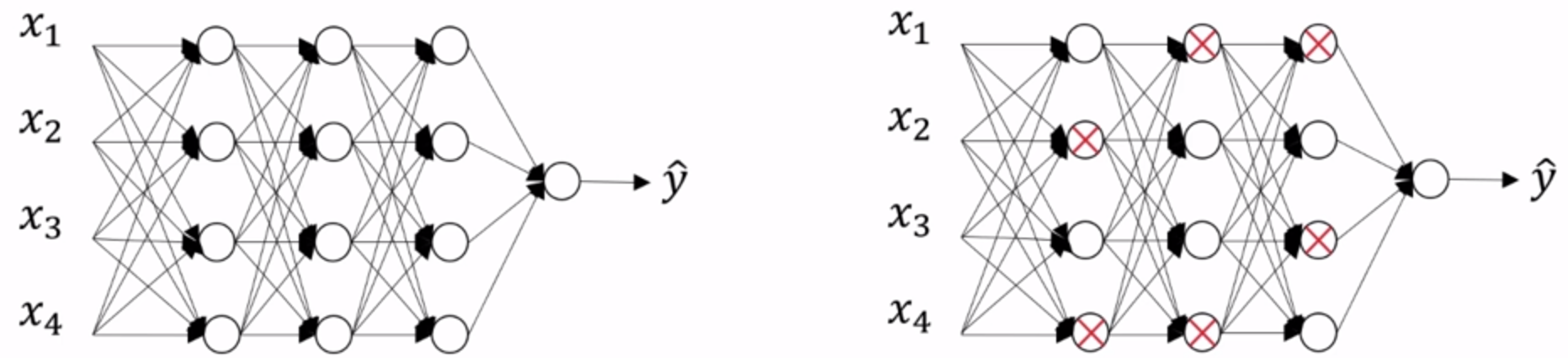
简化连线，得到一个节点更少，规模更小的网络：

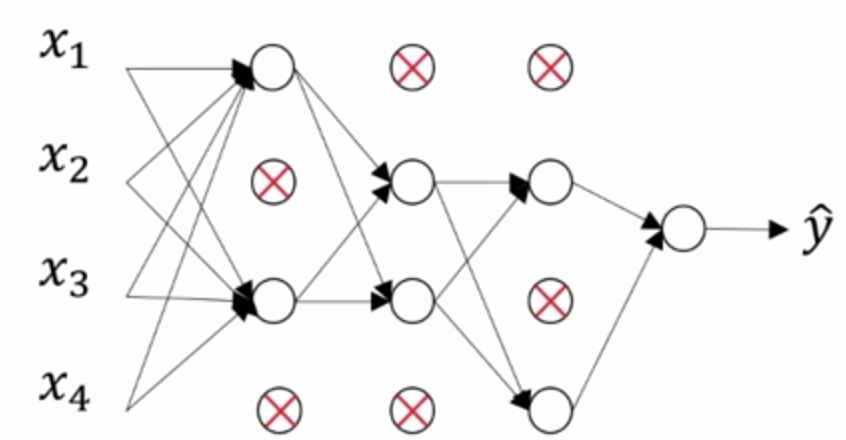
实现代码如下：

对于第3层进行随机失活，keep_prob = 0.8（保留某个隐藏单元的概率，即消除一个隐藏单元的概率为0.2），不同层的keep_prob可以不同.

d3 = np.random.rand(a3.shape[0], a3.shape[1]) < keep_prob

a3 = np.multiply(a3, d3)  #过滤掉失活的节点

a3 = a3 / keep_prob  #弥补过滤掉的20%，使得 a3 的期望值不变

 

（4）其它正则化方法：

① 扩大数据集；

② 提早结束迭代：

 

 

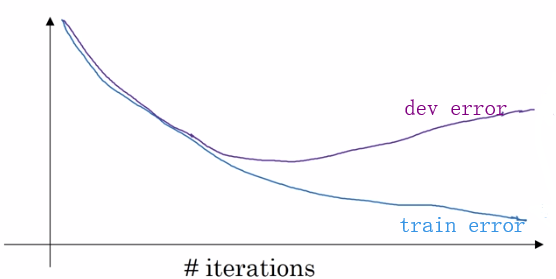
（5）正则化输入：

① 零均值化：

μ = 1 / m * ∑x⁽ⁱ⁾

x = x - μ

 

② 方差归一化：

σ² = 1 / m * ∑(x⁽ⁱ⁾)²

x = x / σ²

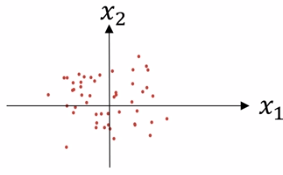
③ 为什么要正则化输入？

非正则化的输入可能导致代价函数的图像偏于细长，如 x1 的取值1-1000，而 x2 的取值仅有0-1. 正则化输入后，代价函数看起来更对称.

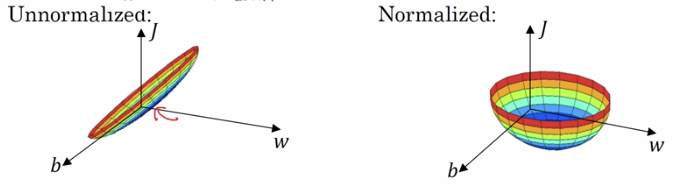
下图可以看到非正则化的梯度下降较为曲折，而正则化的梯度下降较快. 

 

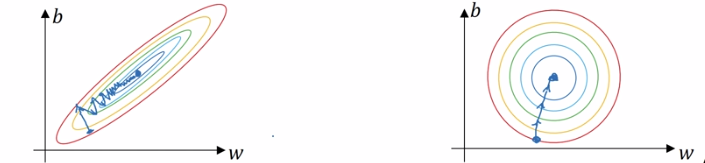
2、Vanishing / Exploding gradients（梯度消散与梯度爆炸）：

（1）举例描述：

 

假设：g(z) = z; b[l] = 0.

y = w^[L]w^[L-1]w^[L-2] ... w^[2]w^[1]x

 

（2）解决方案：权重初始化

由 z = w₁x₁ + w₂x₂ + ... + w_nx_n

随着 n 的增大，期望的 w^[l] 越小，由此设置 Var(w^[l]) = 1/n 或者 2/n（效果更好），即：

w^[l] = np.random.randn(shape) * np.sqrt(2/n^[l-1])

 

3、梯度检验：

（1）梯度的数值逼近：

双边误差公式更准确，可以用来判断 g(θ) 是否实现了函数 f 的偏导.

 

（2）神经网络的梯度检验：

① 将 W^[1]，b^[1]，...，W^[L]，b^[L] 从矩阵转为一个向量 θ；

② 将 dW^[1]，db^[1]，...，dW^[L]，db^[L] 从矩阵转为一个向量 dθ；

③ J = J(θ₁, θ₂, ..., θ_i, ...)

for each i ：

　　dθ_approx^[i] = (J(θ₁, θ₂, ..., θ_i + ε, ...) - J(θ₁, θ₂, ..., θ_i - ε, ...)) / （2 * ε）

　　check dθ_approx^[i] ≈ dθ^[i] by calculate || dθ_approx^[i] - dθ^[i] ||₂  / (|| dθ_approx^[i] ||₂ + || dθ^[i] ||₂)  < 10^-7（或其他误差阈值）

 

（3）梯度检验注意点：

① 检测完关闭梯度检验；

② 检查是否完成了正则化；

③ 不适用于dropout；

④ 检查是否进行了随机初始化.