神经网络和深度学习（二）浅层神经网络

1、计算神经网络的输出（正向传播）：

 

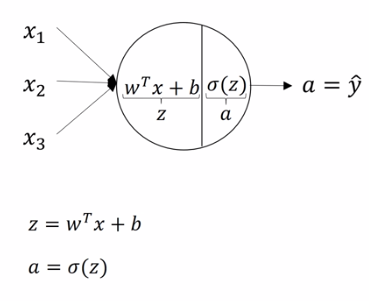
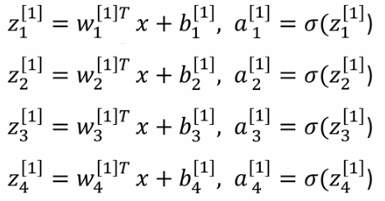
矩阵表示：

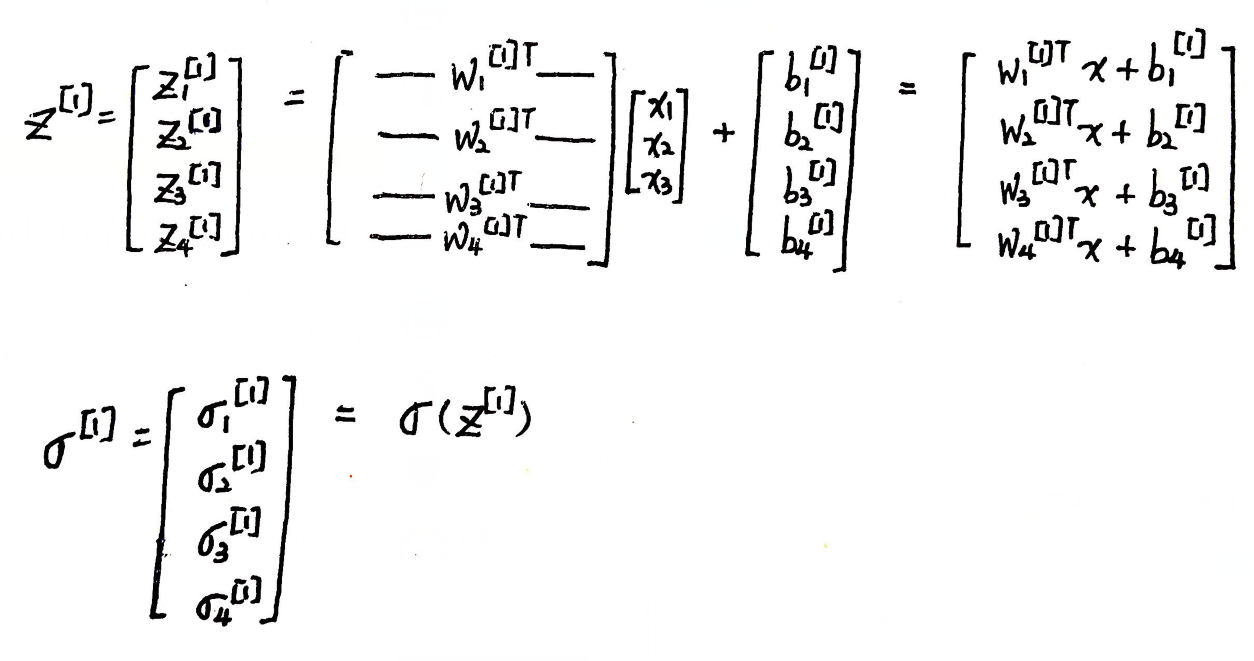
 向量化：

 

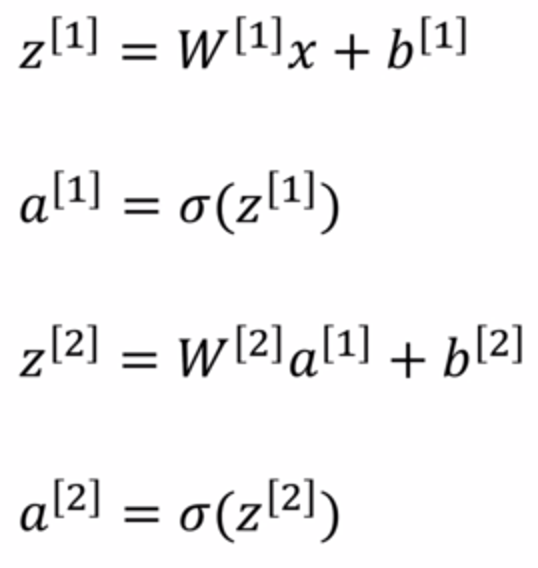
2、多个样本的向量化（正向传播）：

 

3、激活函数：

（1）sigmoid函数仅用于二分分类的情况，较少使用；

a = 1 / (1 + e^-z)

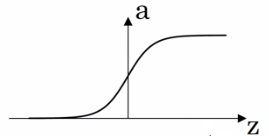
 g'(z) = g(z) * (1 - g(z))

 （2）tanh函数绝大多数情况下优于sigmoid函数；

a = (e^z - e^-z) / (e^z + e^-z)

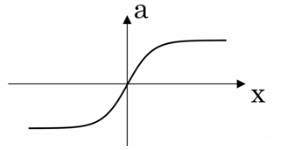
 g'(z) = 1 - g(z)²

（3）ReLU函数是默认的常用激活函数；

a = max(0, z)

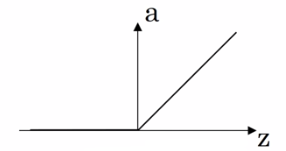
g'(z) = 0   if z < 0

g'(z) = 1   if z ≥ 0

（4）leaking ReLU 带泄露的ReLU函数；

a = max(0.01z, z)

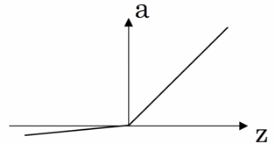
g'(z) = 0.01   if z < 0

g'(z) = 1        if z ≥ 0

 

4、神经网络为什么需要非线性激活函数？

假设使用线性激活函数，即a^[1] = z^[1]

a^[1] = z^[1] = w^[1]x + b^[1]

a^[2] = z^[2] = w^[2]a^[1] + b^[2]

　　= w^[2] * (w^[1]x + b^[1]) + b^[2]

　　= (w^[1]w^[2])x + (w^[2]b^[1] + b^[2])

　　= w'x + b'

可见，神经网络只是把输入线性组合再输出.

一般在回归问题中，可能会使用线性激活函数.

 

5、神经网络中的梯度下降：

 

 

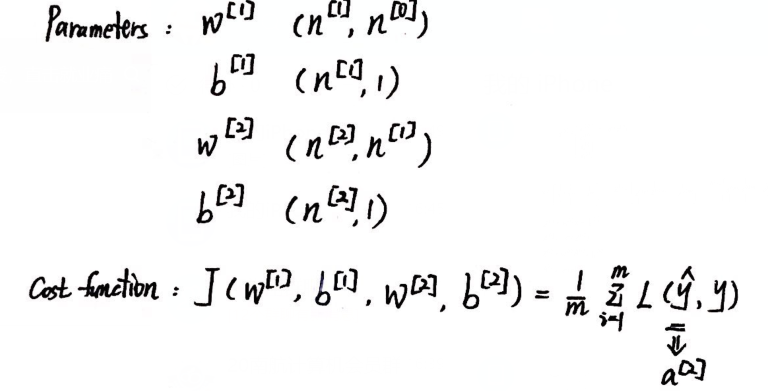
6、直观理解反向传播：

da^[2] = dL/da^[2] = -y/a^[2] + (1-y)/(1-a^[2])

dz^[2] = dL/dz^[2] = dL/da^[2] * da^[2]/dz^[2] = [-y/a^[2] + (1-y)/(1-a^[2])] * a^[2](1-a^[2]) = a^[2]-y

dw^[2] = dL/dw^[2] = dL/dz^[2] * dz^[2]/dw^[2]  = dz^[1]a^[1]T

db^[2] = dL/db^[2] = dL/dz^[2] * dz^[2]/db^[2] = dz^[2]

da^[1] = dL/da^[1] = dL/dz^[2] * dz^[2]/da^[1] = w^[2]Tdz^[2]

dz^[1] = dL/dz^[1] = dL/da^[1] * da^[1]/dz^[1] = w^[2]Tdz^[2] .* g^[1]'(z^[1])

dw^[1] = dL/dw^[1] = dL/dz^[1] * dz^[1]/dw^[1] = dz^[1]x^T

db^[1] = dL/db^[1] = dL/dz^[1] * dz^[1]/db^[1] = dz^[1]

 

7、随机初始化：

如果 w 初始值设置为全0，则隐藏单元的每行值都完全相同，即完全对此. 每个隐藏单元的计算完全相同，使得隐藏单元失去作用.

随机初始化方法：

w^[i] = np.random.randn(...) * 0.01

b^[i] = np.zero(...)

乘上 0.01 是为了避免 z^[i] 太大，导致 a^[i] 太大，使得激活函数处于平缓区域（接近饱和），梯度下降速度慢（g'(z)接近0，dz也接近0）.