机器学习笔记（七）支持向量机

Support vector machine（支持向量机 SVM）

1、推导：

（1）对于逻辑回归，cost函数为：

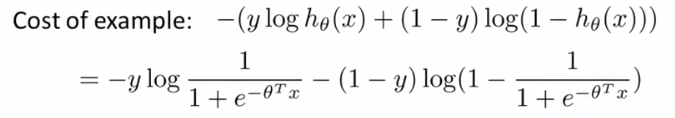
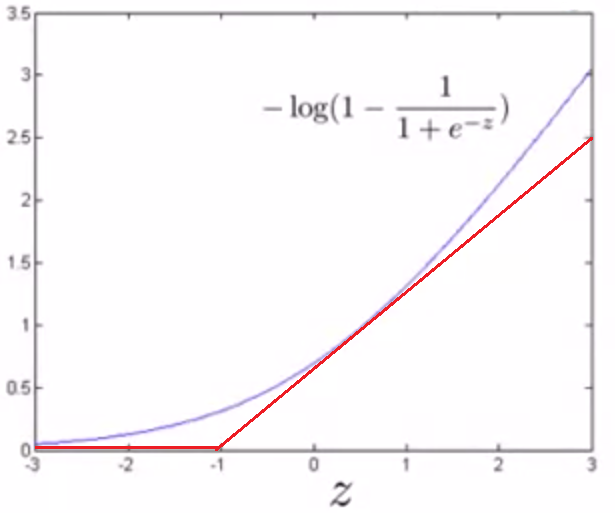
① 当 y = 1时，即 θ^Tx >> 0时 ，cost = - log(1 / (1 + e^-z)) ，图像如下：

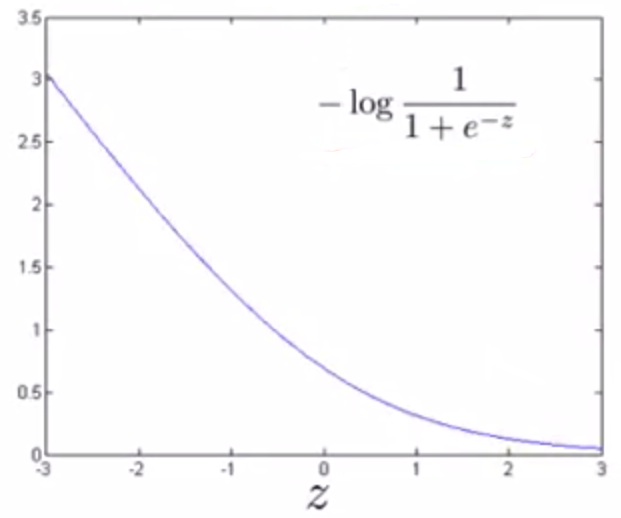
用新的代价函数产生新的曲线：cost₁(z)

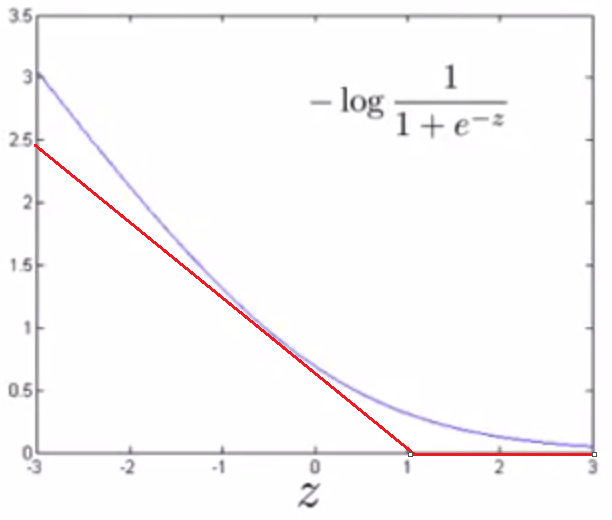
② 当 y = 0时，即 θ^Tx << 0时 ，cost = - log(1 - 1 / (1 + e^-z)) ，图像如下：

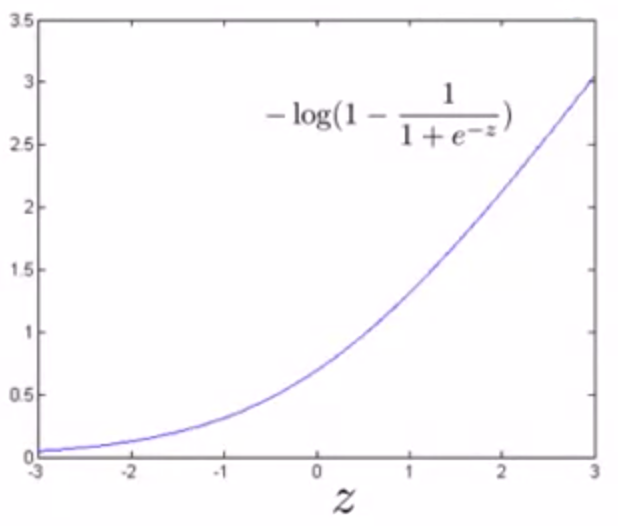
用新的代价函数产生新的曲线：cost₀(z)

 

（2）产生新的目标函数：

 

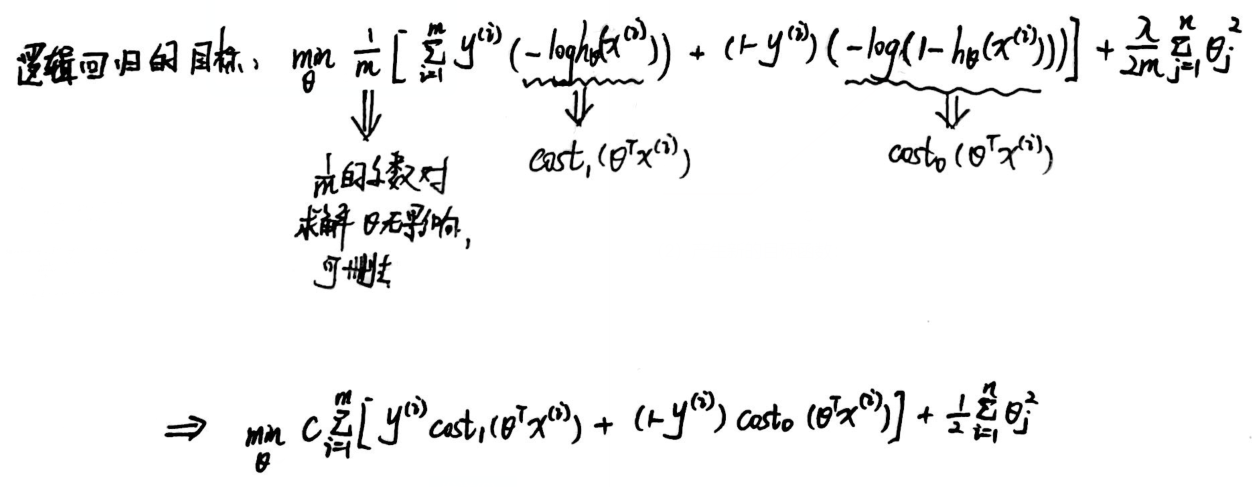
（3）模型修改：

 

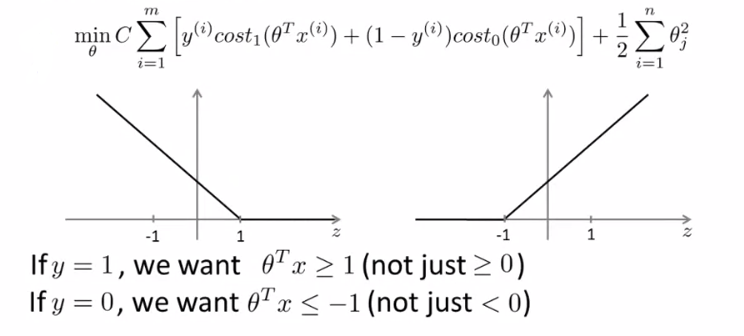
2、Large margin intuition（大间距分类器）：

（1）问题简写：min C * A + B

当 C 比较大时，理想的结果会使得左边的求和式子 A 趋近0，使得问题转化为 min B，即：

 

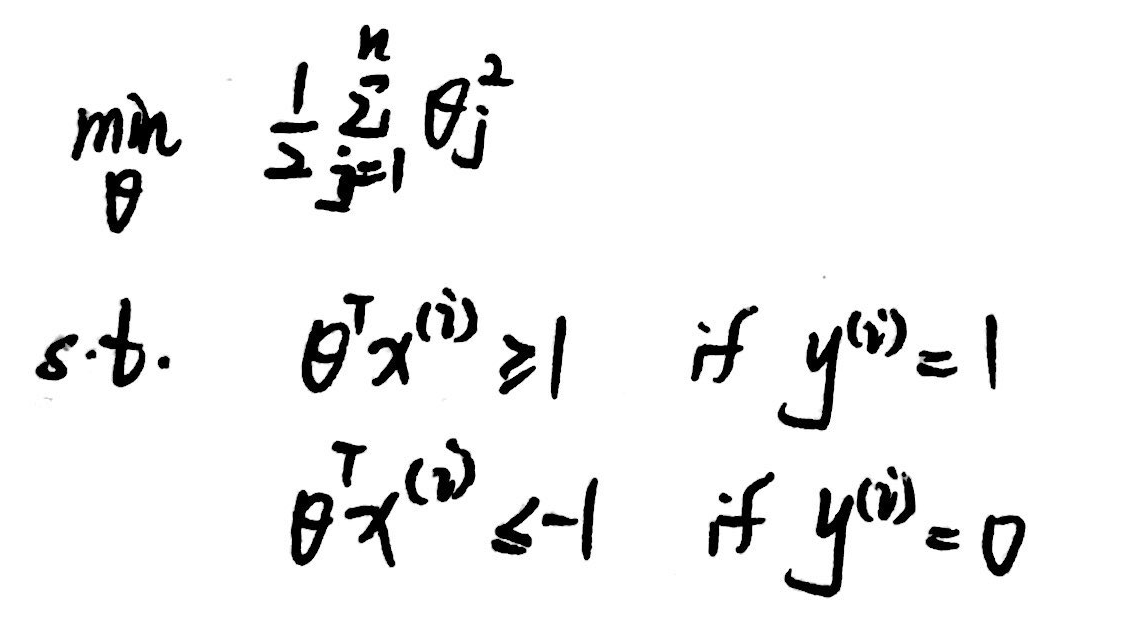
（2）SVM决策边界：

下图的分类问题，有很多种划分方法，但是下面举例的两种分法显然不够科学。

 利用SVM，可以实现最大间距的分类（蓝色线条为决策边界）。

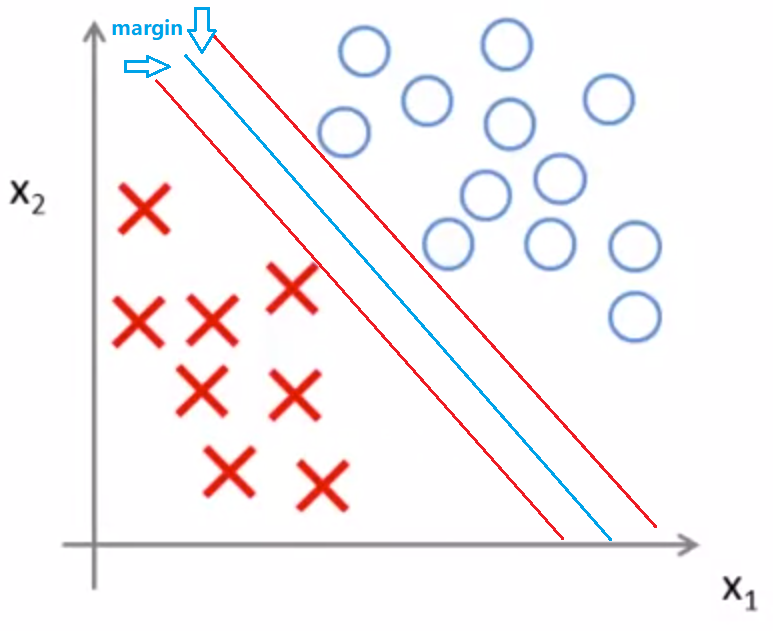
 缺陷：若C特别大，易受到奇异点影响；

 

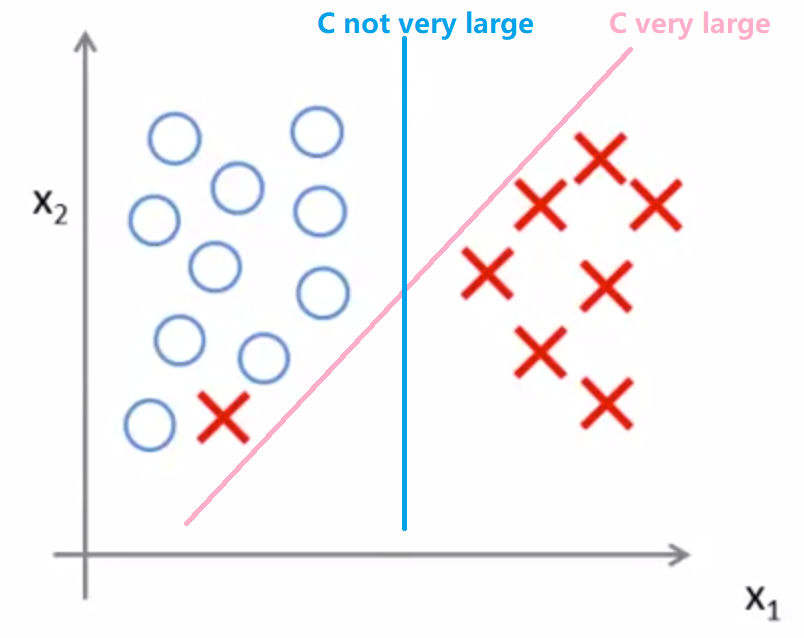
（3）数学原理：

① Vector inner product（向量內积）：

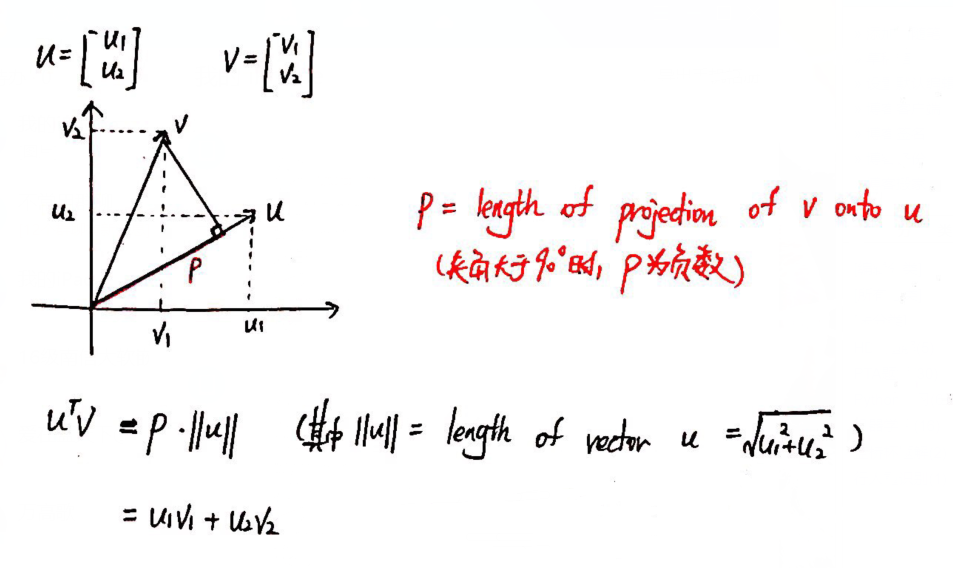
② 简化SVM问题：设置 θ₀ = 0（决策边界必须经过原点）， n = 2

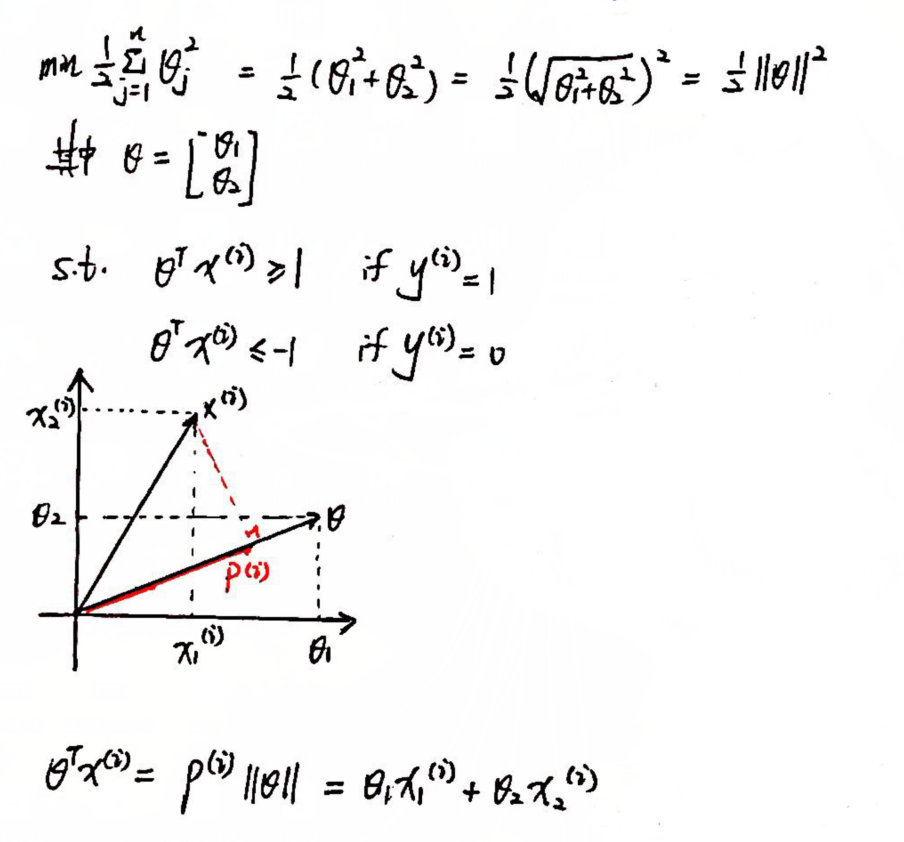
③ 问题转化：

 

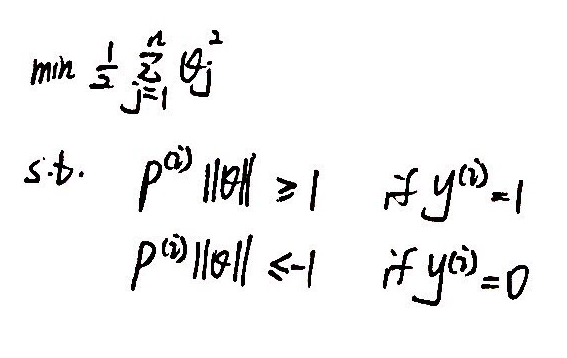
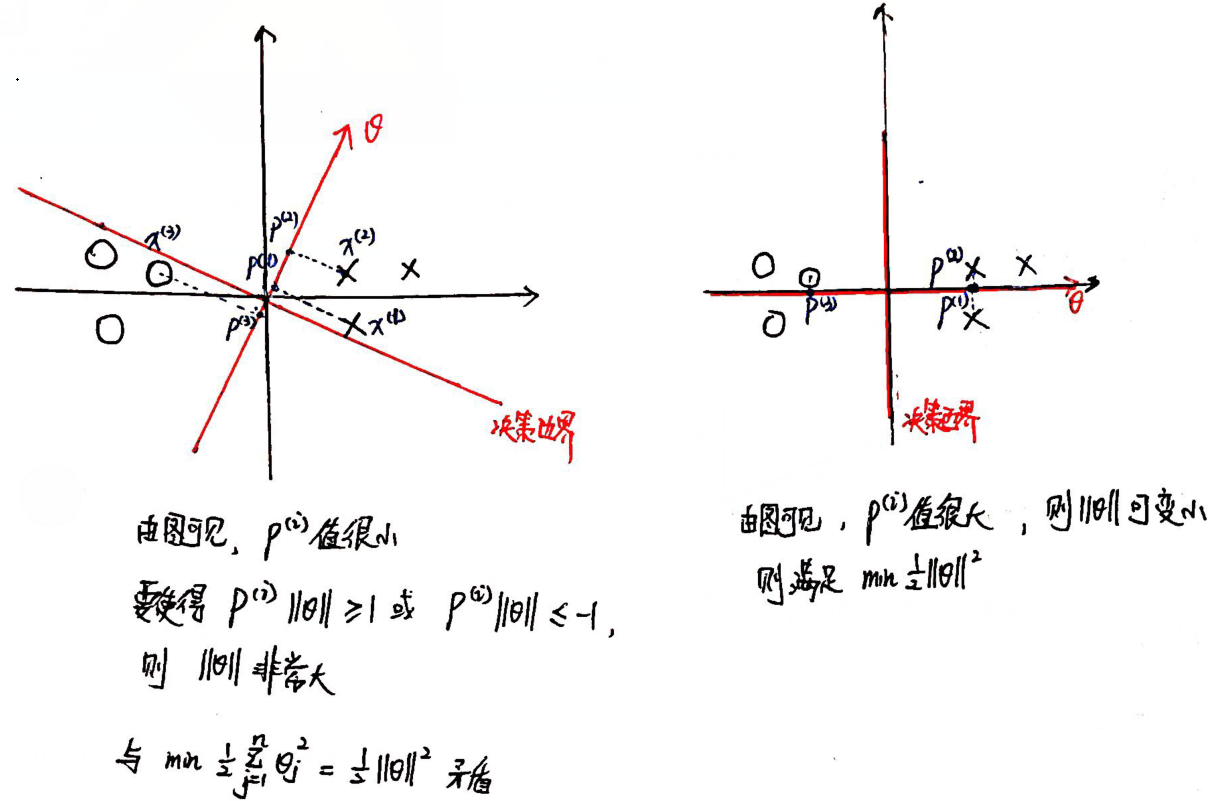
3、Kernels（核函数）：

（1）问题背景：

在进行非线性分类时，使用高次项作为特征变量计算量大，需要更好的方法来构造特征变量。

 

（2）相似度：

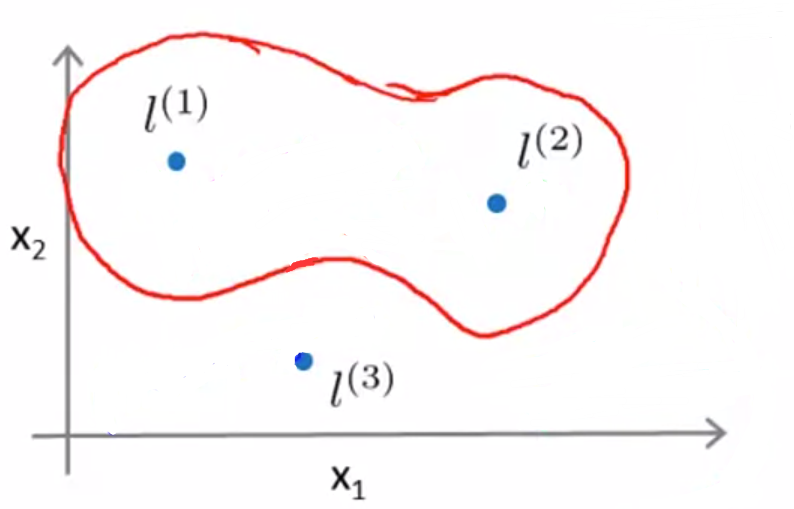
手动取标记点 l⁽¹⁾，l⁽²⁾，l⁽³⁾，度量样本x与标记点之间的相似度：

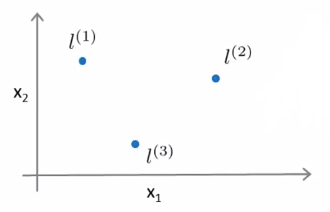
举例与第一个标记点之间的核函数相似度公式（这里采用了高斯核函数）：

如果 x ≈ l⁽¹⁾: f₁ ≈ exp(- 0 / 2σ²) = 1；

如果 x is far from l⁽¹⁾ : f₁ ≈ exp(- large_number² / 2σ²) ≈ 0；

同理，获得f₂，f₃；

 

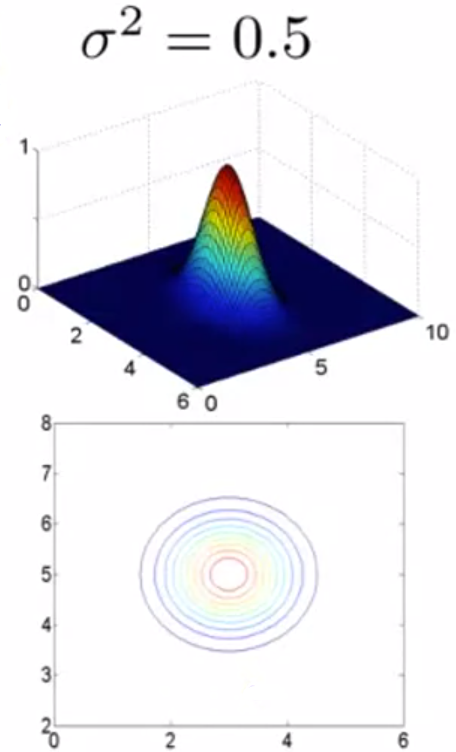
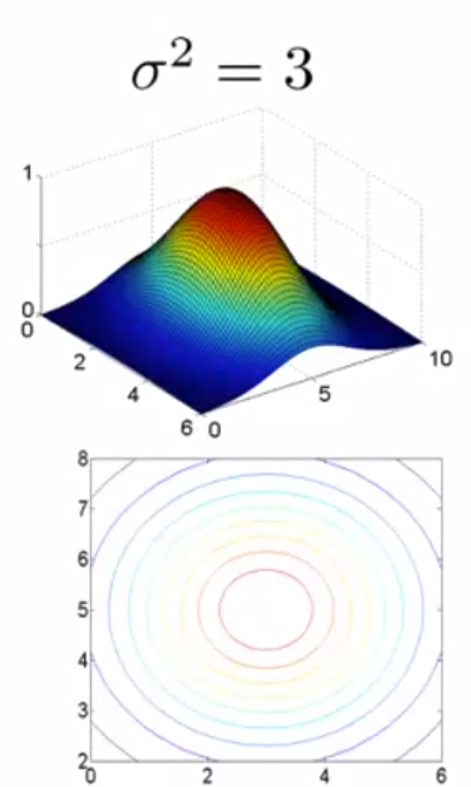
（3）高斯核函数的参数σ：

大σ：特征变量 f 较平稳，高偏差，低方差；

小σ：特征变量 f 较陡，低偏差，高方差。

 

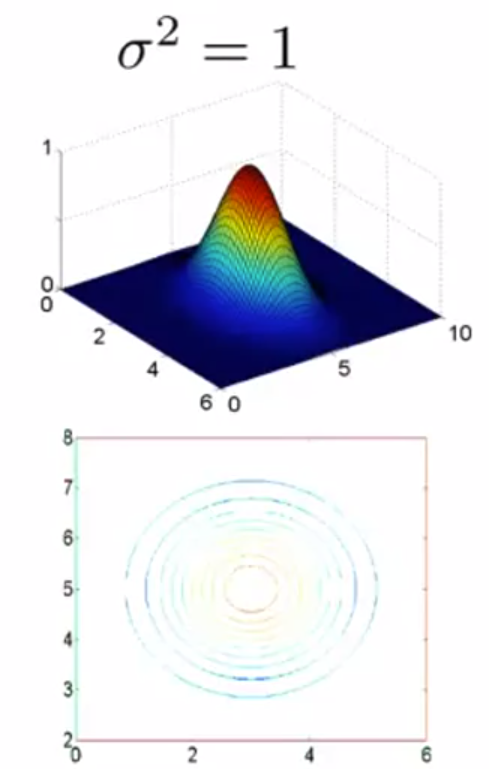
（4）问题转化：

y = 1  when  θ₀ + θ₁f₁ + θ₂f₂ + θ₃f₃ ≥ 0     

y = 0  when  θ₀ + θ₁f₁ + θ₂f₂ + θ₃f₃ ＜0         

 

（5）应用举例：

假设 θ₀ = -0.5，θ₁ = 1，θ₂ = 1，θ₃ = 0；

取靠近 l⁽¹⁾的某一个样本，可以得出 f₁ ≈ 1，f₂ ≈ 0，f₃ ≈ 0. 计算结果得出 0.5 ＞ 0，y = 1.

取靠近 l⁽²⁾的某一个样本，可以得出 f₁ ≈ 0，f₂ ≈ 1，f₃ ≈ 0. 计算结果得出 0.5 ＞ 0，y = 1.

取靠近 l⁽³⁾的某一个样本，可以得出 f₁ ≈ 0，f₂ ≈ 0，f₃ ≈ 1. 计算结果得出 -0.5 ＜ 0，y = 0.

通过大量样本，可以得出决策边界：靠近 l⁽¹⁾ 和 l⁽²⁾ 的样本更可能取1，靠近 l⁽³⁾ 的样本更可能取0.

 

（6）SVM with Kernels：

① 直接把样本点作为标记点，如 l⁽¹⁾ = x⁽¹⁾ ，l⁽²⁾ = x⁽²⁾，...，l^(m) = x^(m)；

② 对于训练集 (x⁽ⁱ⁾, y⁽ⁱ⁾)：

f₁⁽ⁱ⁾ = similarity(x⁽ⁱ⁾, l⁽¹⁾)；

f₂⁽ⁱ⁾ = similarity(x⁽ⁱ⁾, l⁽²⁾)；

...

f_m⁽ⁱ⁾ = similarity(x⁽ⁱ⁾, l^(m))；

获得特征变量 f（m+1 维特征向量）；

③ 预测：

predict y = 1 if θ^Tf ≥ 0；

predict y = 0 if θ^Tf ＜ 0；

④ 训练：（注：求和变量 n 实际等于 m ）

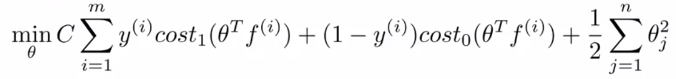
⑤ 参数 C 的选择：

C太大（即 lambda 太小）：低偏差，高方差；

C太小（即 lambda 太大）：高偏差，低方差；

 

4、SVM的使用：

（1）使用SVM软件包求解 θ ：liblinear、libsvm .

（2）自主操作：

① 设置参数C.

② 选择核函数计算特征量（没有核函数即为线性核函数）.

选择的核函数必须满足Mercer's Theorem（默塞尔定理）.

除了线性核函数和高斯核函数，还有满足默塞尔定理的核函数有：

多项式核函数： k(x, l) = (x^Tl + constant)^degree 其中constant、degree是参数； 

字符串核函数、卡房核函数、直方图交叉核函数等.

③ 对于大小差距很大的特征量，需要进行归一化处理.

 

5、逻辑回归 vs 支持向量机：

当 n 对与训练集大小来说较大时（例如，n = 10000，m = 10~1000），使用逻辑回归或者线性核函数SVM；

当 n 较小，而 m 大小适中时（例如，n = 1~1000，m = 10~10000），使用高斯核函数SVM；

当 n 较小，m较大时（例如，n = 1~1000，m = 50000+），新增更多特征，再使用逻辑回归或者线性核函数SVM.