机器学习作业（五）机器学习算法的选择与优化——Matlab实现

题目下载【传送门】

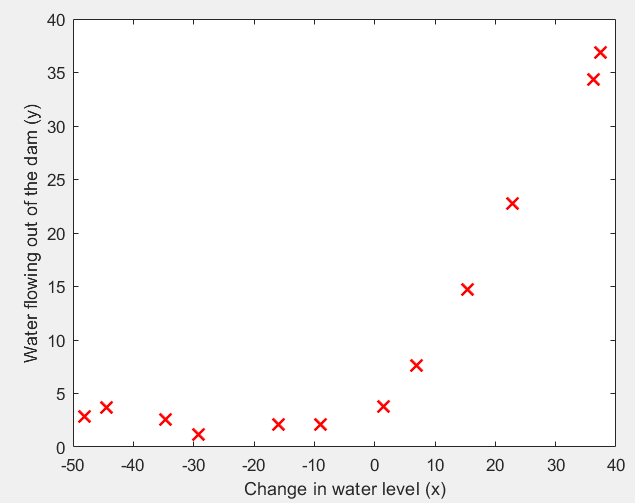
第1步：读取数据文件，并可视化：

% Load from ex5data1: 
% You will have X, y, Xval, yval, Xtest, ytest in your environment
load ('ex5data1.mat');

% m = Number of examples
m = size(X, 1);

% Plot training data
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');

运行结果：

 

第2步：实现linearRegCostFunction函数，采用线性回归和正规化求 J 和 grad：

function [J, grad] = linearRegCostFunction(X, y, theta, lambda)

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

theta_copy = theta;
theta_copy(1, :) = 0
J = 1 / (2 * m) * sum((X * theta - y) .^ 2) + lambda / (2 * m) * sum(theta_copy .^ 2);
grad = 1 / m * (X' * (X * theta - y)) + lambda / m * theta_copy;

grad = grad(:);

end

 

第3步：实现训练函数trainLinearReg：

function [theta] = trainLinearReg(X, y, lambda)

% Initialize Theta
initial_theta = zeros(size(X, 2), 1); 

% Create "short hand" for the cost function to be minimized
costFunction = @(t) linearRegCostFunction(X, y, t, lambda);

% Now, costFunction is a function that takes in only one argument
options = optimset('MaxIter', 200, 'GradObj', 'on');

% Minimize using fmincg
theta = fmincg(costFunction, initial_theta, options);

end

 

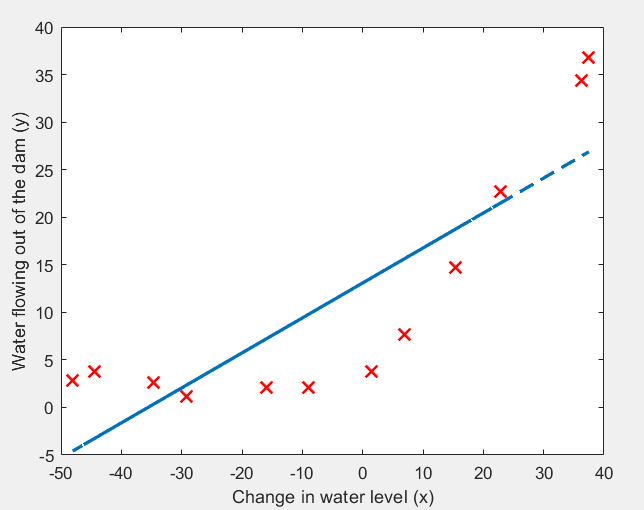
使用 lambda = 0，测试结果：

%  Train linear regression with lambda = 0
lambda = 0;
[theta] = trainLinearReg([ones(m, 1) X], y, lambda);

%  Plot fit over the data
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
hold on;
plot(X, [ones(m, 1) X]*theta, '--', 'LineWidth', 2)
hold off;

运行结果：很显然，采用 y = θ₀ + θ₁x 欠拟合。

 

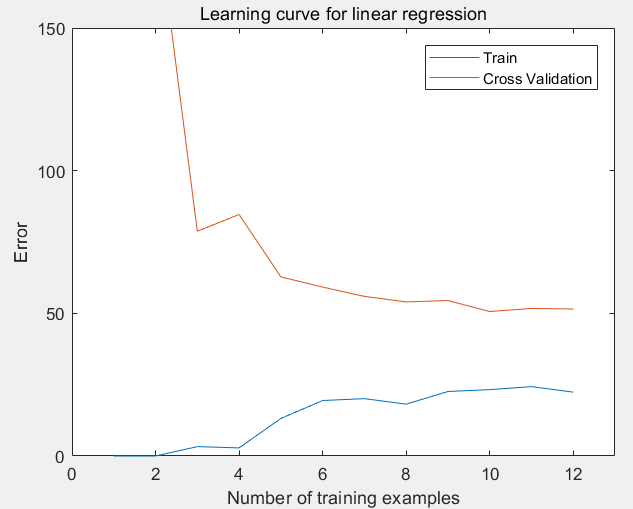
第4步：绘制关于训练集数量的学习曲线，在lambda = 0 的情况下，观察训练集的大小1 ~ m给训练误差和验证误差的影响：

lambda = 0;
[error_train, error_val] = ...
    learningCurve([ones(m, 1) X], y, ...
                  [ones(size(Xval, 1), 1) Xval], yval, ...
                  lambda);

plot(1:m, error_train, 1:m, error_val);
title('Learning curve for linear regression')
legend('Train', 'Cross Validation')
xlabel('Number of training examples')
ylabel('Error')
axis([0 13 0 150])

　

其中学习曲线函数learningCurve：

function [error_train, error_val] = ...
    learningCurve(X, y, Xval, yval, lambda)

for i = 1:m,
    X_temp = X(1:i, :);
    y_temp = y(1:i);
    theta = trainLinearReg(X_temp, y_temp, lambda);
    error_train(i) = 1 / (2 * i) * sum((X_temp * theta - y_temp) .^ 2);
    error_val(i) = 1 / (2 * m) * sum((Xval * theta - yval) .^ 2);
end

end

运行结果：随着训练集的扩大，训练误差和验证误差均比较大，是高误差问题（欠拟合）。

 

第5步：为了解决欠拟合问题，需要改进特征，下面对训练、交叉验证、测试三组数据进行特征扩充和均值归一化：

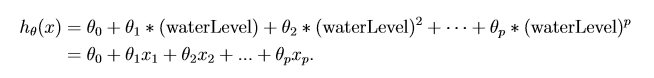
p = 8;

% Map X onto Polynomial Features and Normalize
X_poly = polyFeatures(X, p);
[X_poly, mu, sigma] = featureNormalize(X_poly);  % Normalize
X_poly = [ones(m, 1), X_poly];                   % Add Ones

% Map X_poly_test and normalize (using mu and sigma)
X_poly_test = polyFeatures(Xtest, p);
X_poly_test = bsxfun(@minus, X_poly_test, mu);
X_poly_test = bsxfun(@rdivide, X_poly_test, sigma);
X_poly_test = [ones(size(X_poly_test, 1), 1), X_poly_test];         % Add Ones

% Map X_poly_val and normalize (using mu and sigma)
X_poly_val = polyFeatures(Xval, p);
X_poly_val = bsxfun(@minus, X_poly_val, mu);
X_poly_val = bsxfun(@rdivide, X_poly_val, sigma);
X_poly_val = [ones(size(X_poly_val, 1), 1), X_poly_val];           % Add Ones

fprintf('Normalized Training Example 1:\n');
fprintf('  %f  \n', X_poly(1, :));

　

其中ployFeatures函数实现特征值扩充的作用：

function [X_poly] = polyFeatures(X, p)

% You need to return the following variables correctly.
X_poly = zeros(numel(X), p);

X_poly(:, 1) = X(:, 1);
for i = 2:p,
    X_poly(:, i) = X_poly(:, i-1) .* X(:, 1);
end

end

 

其中featureNormalize函数实现均值归一化功能：

function [X_norm, mu, sigma] = featureNormalize(X)

mu = mean(X);
X_norm = bsxfun(@minus, X, mu);

sigma = std(X_norm);
X_norm = bsxfun(@rdivide, X_norm, sigma);

end

 

第6步：设置不同的lambda，查看拟合结果和学习曲线：

lambda = 0;
[theta] = trainLinearReg(X_poly, y, lambda);

% Plot training data and fit
figure(1);
plot(X, y, 'rx', 'MarkerSize', 10, 'LineWidth', 1.5);
plotFit(min(X), max(X), mu, sigma, theta, p);
xlabel('Change in water level (x)');
ylabel('Water flowing out of the dam (y)');
title (sprintf('Polynomial Regression Fit (lambda = %f)', lambda));

figure(2);
[error_train, error_val] = ...
    learningCurve(X_poly, y, X_poly_val, yval, lambda);
plot(1:m, error_train, 1:m, error_val);

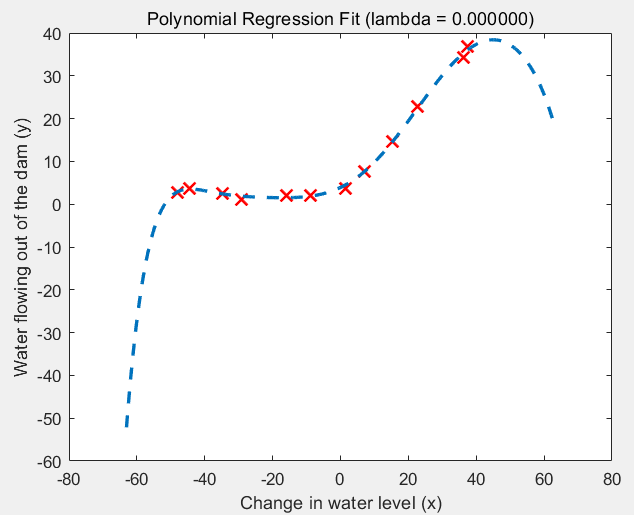
title(sprintf('Polynomial Regression Learning Curve (lambda = %f)', lambda));
xlabel('Number of training examples')
ylabel('Error')
axis([0 13 0 100])
legend('Train', 'Cross Validation')

（1）lambda = 0的情况：过拟合

 

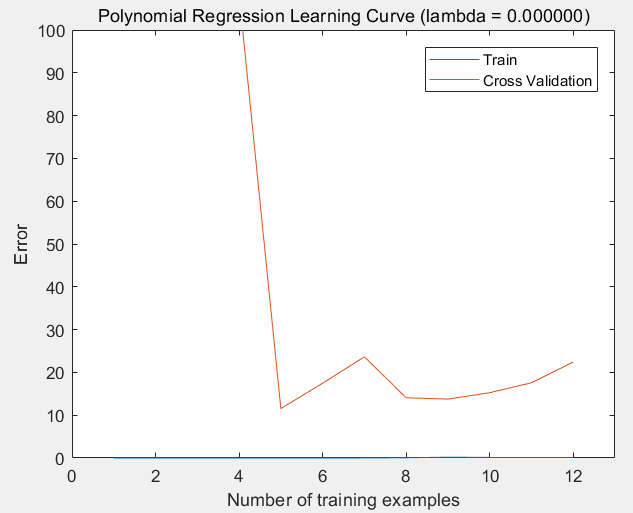
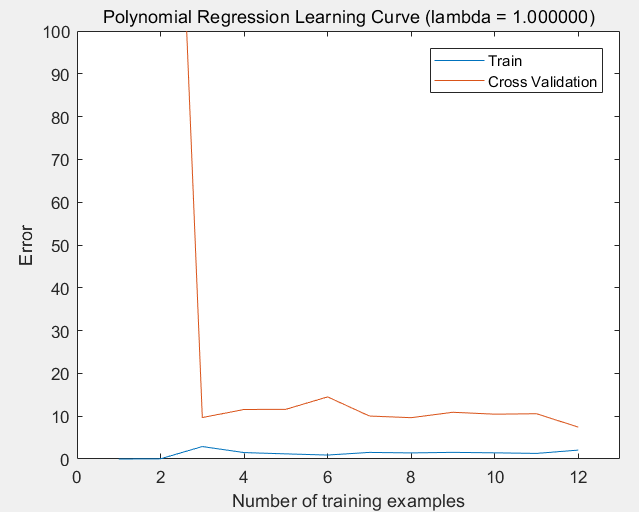
（2）lambda = 1的情况：过拟合

 

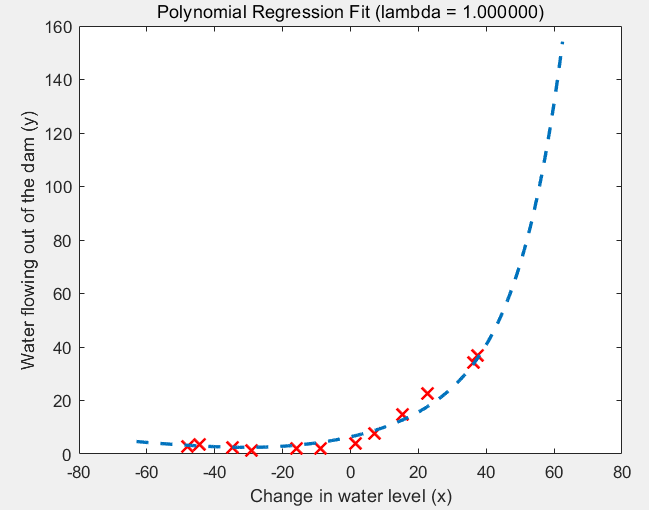
（3）lambda = 100的情况：欠拟合

 

 

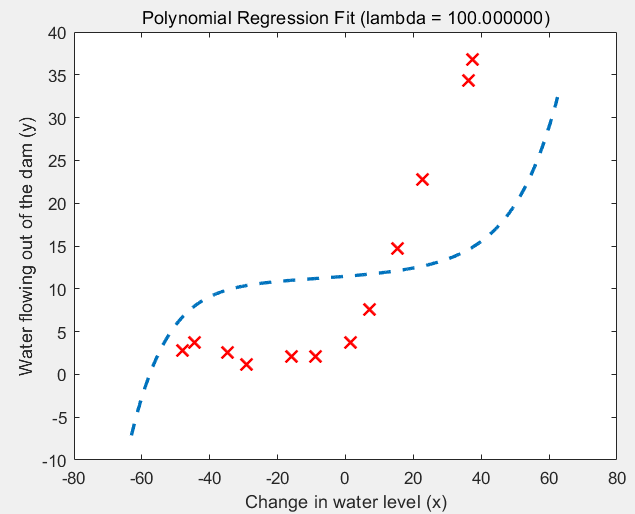
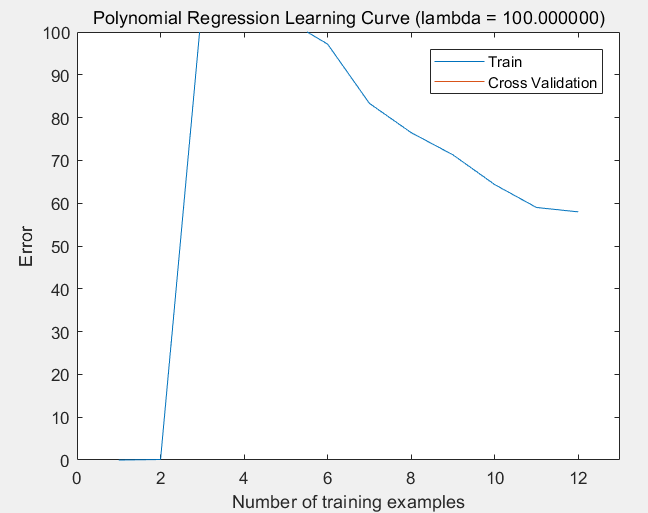
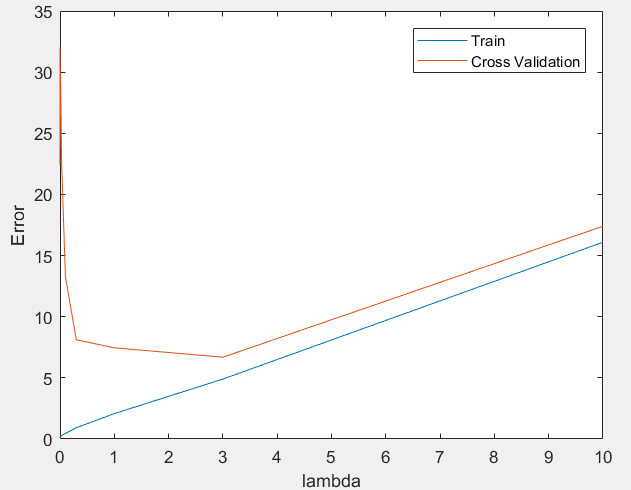
第7步：绘制关于lambda的学习曲线，选择最优的lambda：

[lambda_vec, error_train, error_val] = ...
    validationCurve(X_poly, y, X_poly_val, yval);

close all;
plot(lambda_vec, error_train, lambda_vec, error_val);
legend('Train', 'Cross Validation');
xlabel('lambda');
ylabel('Error');

 

其中validationCurve函数：

function [lambda_vec, error_train, error_val] = ...
    validationCurve(X, y, Xval, yval)

m = size(X, 1)
for i = 1:size(lambda_vec),
    lambda = lambda_vec(i);
    theta = trainLinearReg(X, y, lambda);
    error_train(i) = 1 / (2 * m) * sum((X * theta - y) .^ 2);
    error_val(i) = 1 / (2 * m) * sum((Xval * theta - yval) .^ 2);
end

end

运行结果：可以看出，在lambda在[2, 3]上有较好的效果。