机器学习作业(四)神经网络参数的拟合——Python(numpy)实现
题目下载【传送门】
题目简述:识别图片中的数字,训练该模型,求参数θ。
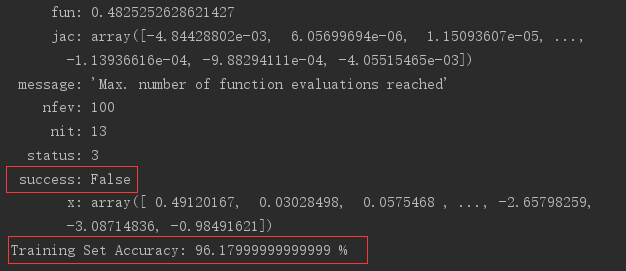
出现了一个问题:虽然训练的模型能够有很好的预测准确率,但是使用minimize函数时候始终无法成功,无论设计的迭代次数有多大,如下图:
1 import numpy as np 2 import scipy.io as scio 3 import matplotlib.pyplot as plt 4 import scipy.optimize as op 5 6 # X:5000*400 7 # Y:5000*10 8 # a1:5000*401(后5000*400) 9 # z2:5000*25 10 # a2:5000*26(后5000*25) 11 # z3:5000*10 12 # a3:5000*10 13 # Theta1:25*401 14 # Theta2:10*26 15 # delta3:5000*10 16 # delta2:5000*25 17 # bigDelta1:25*401 18 # bigDelta2:10*26 19 # Theta1_grad:25*401 20 # Theta2_grad:10*26 21 22 23 #显示图片数据 24 def displayData(X): 25 m = np.size(X, 0) #X的行数,即样本数量 26 n = np.size(X, 1) #X的列数,即单个样本大小 27 example_width = int(np.round(np.sqrt(n))) #单张图片宽度 28 example_height = int(np.floor(n / example_width)) #单张图片高度 29 display_rows = int(np.floor(np.sqrt(m))) #显示图中,一行多少张图 30 display_cols = int(np.ceil(m / display_rows)) #显示图中,一列多少张图片 31 pad = 1 #图片间的间隔 32 display_array = - np.ones((pad + display_rows * (example_height + pad), 33 pad + display_cols * (example_width + pad))) #初始化图片矩阵 34 curr_ex = 0 #当前的图片计数 35 #将每张小图插入图片数组中 36 for j in range(0, display_rows): 37 for i in range(0, display_cols): 38 if curr_ex >= m: 39 break 40 max_val = np.max(abs(X[curr_ex, :])) 41 jstart = pad + j * (example_height + pad) 42 istart = pad + i * (example_width + pad) 43 display_array[jstart: (jstart + example_height), istart: (istart + example_width)] = \ 44 np.array(X[curr_ex, :]).reshape(example_height, example_width) / max_val 45 curr_ex = curr_ex + 1 46 if curr_ex >= m: 47 break 48 display_array = display_array.T 49 plt.imshow(display_array,cmap=plt.cm.gray) 50 plt.axis('off') 51 plt.show() 52 53 54 #计算hθ(z) 55 def sigmoid(z): 56 g = 1.0 / (1.0 + np.exp(-z)) 57 return g 58 59 60 #初始化Θ,保持在[-ε,ε] 61 def randInitializeWeights(sizeList): 62 epsilon_init = 0.12 63 theta1_lx = sizeList['theta1_lx'] 64 theta1_ly = sizeList['theta1_ly'] 65 theta2_lx = sizeList['theta2_lx'] 66 theta2_ly = sizeList['theta2_ly'] 67 theta_size = theta1_lx * theta1_ly + theta2_lx * theta2_ly 68 W = np.random.uniform(-epsilon_init, epsilon_init, theta_size) 69 return W 70 71 72 #把一维的矩阵改写为多维 73 def changeForm(theta_vector, theta1_lx, theta1_ly, theta2_lx, theta2_ly): 74 theta1 = np.array(theta_vector[0: theta1_lx * theta1_ly]).reshape(theta1_lx, theta1_ly) 75 theta2 = np.array(theta_vector[theta1_lx * theta1_ly: theta1_lx * theta1_ly + theta2_lx * theta2_ly])\ 76 .reshape(theta2_lx, theta2_ly) 77 theta = {'Theta1': theta1, 'Theta2': theta2} 78 return theta 79 80 81 #计算正向激励的参数a 82 def computeA(nn_params, X): 83 theta1 = nn_params['Theta1'] 84 theta2 = nn_params['Theta2'] 85 m = np.size(X, 0) 86 87 #第二层计算 88 one = np.ones(m) 89 a1 = np.insert(X, 0, values=one, axis=1) 90 a2 = sigmoid(np.dot(a1, theta1.T)) 91 #第三层计算 92 one = np.ones(np.size(a2, 0)) 93 a2 = np.insert(a2, 0, values=one, axis=1) 94 a3 = sigmoid(np.dot(a2, theta2.T)) 95 a_res = {'a1': a1, 'a2': a2, 'a3': a3} 96 return a_res 97 98 99 #计算g'(z) 100 def sigmoidGradient(z): 101 g = np.multiply(sigmoid(z), 1 - sigmoid(z)) 102 return g 103 104 105 #计算 J 106 def nnCostFunction(nn_params, X, Y, lamb, sizeList): 107 theta = changeForm(nn_params, 108 sizeList['theta1_lx'], sizeList['theta1_ly'], 109 sizeList['theta2_lx'], sizeList['theta2_ly']) 110 theta1 = theta['Theta1'] 111 theta2 = theta['Theta2'] 112 m = np.size(X, 0) 113 a_res = computeA(theta, X) 114 a3 = a_res['a3'] 115 #计算J 116 J = 1 / m * np.sum(-np.multiply(Y, np.log(a3)) - np.multiply((1 - Y), np.log(1 - a3))) 117 #规格化 118 theta1_copy = theta1[:, 1:] 119 theta2_copy = theta2[:, 1:] 120 J = J + lamb / (2 * m) * (np.sum(theta1_copy ** 2) + np.sum(theta2_copy ** 2)) 121 print(J) 122 return J 123 124 125 #计算 D 126 def nnGradient(nn_params, X, Y, lamb, sizeList): 127 theta = changeForm(nn_params, 128 sizeList['theta1_lx'], sizeList['theta1_ly'], 129 sizeList['theta2_lx'], sizeList['theta2_ly']) 130 theta1 = theta['Theta1'] 131 theta2 = theta['Theta2'] 132 m = np.size(X, 0) 133 a_res = computeA(theta, X) 134 a1 = a_res['a1'] 135 a2 = a_res['a2'] 136 a3 = a_res['a3'] 137 theta1_copy = theta1[:, 1:] 138 theta2_copy = theta2[:, 1:] 139 #计算δ 140 delta3 = a3 - Y 141 delta2 = np.multiply(np.dot(delta3, theta2_copy), sigmoidGradient(np.dot(a1, theta1.T))) 142 #计算Δ 143 bigDeilta1 = np.dot(delta2.T, a1) 144 bigDeilta2 = np.dot(delta3.T, a2) 145 #计算D 146 theta1_grad = bigDeilta1 / m + lamb / m * theta1 147 theta2_grad = bigDeilta2 / m + lamb / m * theta2 148 theta1_grad[:, 0] = bigDeilta1[:, 0] / m 149 theta2_grad[:, 0] = bigDeilta2[:, 0] / m 150 #当使用高级优化方法来优化神经网络时,需要将多个参数矩阵展开,才能传入优化函数 151 grad = np.r_[theta1_grad.flatten(), theta2_grad.flatten()] 152 # print(np.size(grad)) 153 return grad 154 155 156 #测试参数的初始化 157 def debugInitializeWeights(L_out, L_in): 158 W = np.arange(1, L_out * (L_in + 1)+1) 159 W = np.sin(W) 160 W = np.array(W).reshape(L_out, (L_in + 1)) / 10; 161 return W 162 163 164 #数值方法计算梯度 165 def computeNumericalGradient(theta, X, Y ,lamb, sizeList): 166 numgrad = np.zeros(np.size(theta)) 167 perturb = np.zeros(np.size(theta)) 168 e = 1e-4 169 for p in range(0, np.size(theta)): 170 perturb[p] = e 171 theta_minus = theta - perturb 172 theta_plus = theta + perturb 173 loss1 = nnCostFunction(theta_minus, X, Y, lamb, sizeList) 174 loss2 = nnCostFunction(theta_plus, X, Y, lamb, sizeList) 175 numgrad[p] = (loss2 - loss1) / (2 * e) 176 perturb[p] = 0 177 return numgrad 178 179 180 #梯度检测函数 181 def checkNNGradients(lamb): 182 #设置测试参数 183 input_layer_size = 3; 184 hidden_layer_size = 5; 185 num_labels = 3; 186 lamb = 1 187 m = 5; 188 sizeList = {'theta1_lx': hidden_layer_size, 189 'theta1_ly': input_layer_size + 1, 190 'theta2_lx': num_labels, 191 'theta2_ly': hidden_layer_size + 1} # 保存θ大小的参数 192 theta1 = debugInitializeWeights(hidden_layer_size, input_layer_size) 193 theta2 = debugInitializeWeights(num_labels, hidden_layer_size) 194 theta = np.r_[theta1.flatten(), theta2.flatten()] 195 X = debugInitializeWeights(m, input_layer_size - 1) 196 y = np.random.randint(0, num_labels, (m, 1)) 197 # 对y进行改写,改为 m*num_labels 规格的矩阵 198 Y = np.zeros((m, num_labels)) 199 for i in range(0, m): 200 Y[i, y[i, 0]] = 1 201 grad = nnGradient(theta, X, Y, lamb, sizeList) 202 numGrad = computeNumericalGradient(theta, X, Y, lamb, sizeList) 203 diff = np.linalg.norm(numGrad - grad) / np.linalg.norm(numGrad + grad) 204 print('check NN Gradient: diff = ', diff) 205 206 207 #使用模型进行预测 208 def predict(theta1, theta2, X): 209 m = np.size(X,0) 210 p = np.zeros((np.size(X, 0), 1)) 211 #第二层计算 212 one = np.ones(m) 213 X = np.insert(X, 0, values=one, axis=1) 214 a2 = sigmoid(np.dot(X, theta1.T)) 215 #第三层计算 216 one = np.ones(np.size(a2,0)) 217 a2 = np.insert(a2, 0, values=one, axis=1) 218 a3 = sigmoid(np.dot(a2, theta2.T)) 219 p = a3.argmax(axis=1) + 1 #y的值为1-10,所以此处0-9要加1 220 return p.flatten() 221 222 223 # ——————————————主函数———————————————————— 224 #初始化数据 225 input_layer_size = 400 226 hidden_layer_size = 25 227 num_labels = 10 228 sizeList = {'theta1_lx': hidden_layer_size, 229 'theta1_ly': input_layer_size + 1, 230 'theta2_lx': num_labels, 231 'theta2_ly': hidden_layer_size + 1} #保存θ大小的参数 232 lamb = 1 233 234 #加载数据文件 235 data = scio.loadmat('ex4data1.mat') 236 X = data['X'] 237 m = np.size(X, 0) 238 y = data['y'] 239 # 对y进行改写,改为5000*10规格的矩阵,第0-9个位置分别表示1,2,...,9,0 240 Y = np.zeros((m, num_labels)) 241 for i in range(0, m): 242 Y[i, y[i, 0] - 1] = 1 243 rand_indices = np.random.randint(0, m, 100) 244 sel = X[rand_indices, :] 245 displayData(sel) 246 247 #测试数据θ 248 theta = scio.loadmat('ex4weights.mat') 249 theta1 = theta['Theta1'] 250 theta2 = theta['Theta2'] 251 nn_theta = np.r_[theta1.flatten(), theta2.flatten()] 252 253 #测试nnCostFunction 254 # J = nnCostFunction(nn_theta, X, Y, 3, sizeList) 255 # print(J) 256 257 #测试nnGradient 258 print(nnGradient(nn_theta, X, Y, lamb, sizeList)) 259 260 #初始化参数 261 nn_params = randInitializeWeights(sizeList) 262 263 # 梯度检测 264 # checkNNGradients(lamb) 265 266 # 训练模型 267 res = op.minimize(fun=nnCostFunction, 268 x0=nn_params, 269 args=(X, Y, lamb, sizeList), 270 method='TNC', 271 jac=nnGradient, 272 options={'maxiter': 100}) 273 print(res) 274 275 #计算准确率 276 all_theta = changeForm(res.x, sizeList['theta1_lx'], sizeList['theta1_ly'], 277 sizeList['theta2_lx'], sizeList['theta2_ly']) 278 res_theta1 = all_theta['Theta1'] 279 res_theta2 = all_theta['Theta2'] 280 pred = predict(res_theta1, res_theta2, X) 281 acc = np.mean(pred == y.flatten())*100 282 print('Training Set Accuracy:',acc,'%') 283 284 #显示中间隐藏层 285 displayData(res_theta1[:, 1:])
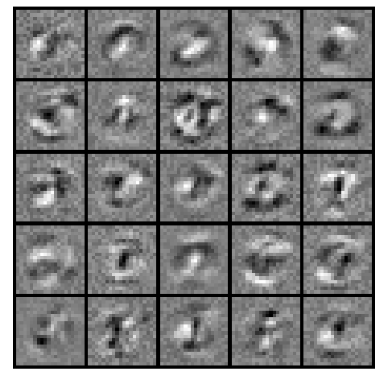
隐藏层显示: