机器学习笔记（五）神经网络参数的拟合
Cost function（代价函数）
1、参数表示：
m 个训练样本：{(x(1), y(1)), (x(2), y(2)), ..., (x(m), y(m))}
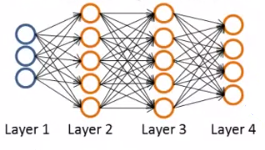
神经网络的层数：L
l 层的神经元数量（不计入偏置单元）：Sl
2、两种分类问题：
（1）Binary classification（二元分类）：
y = 0 or 1
只有一个输出单元 / hθ(x)为一个实数 / SL = 1
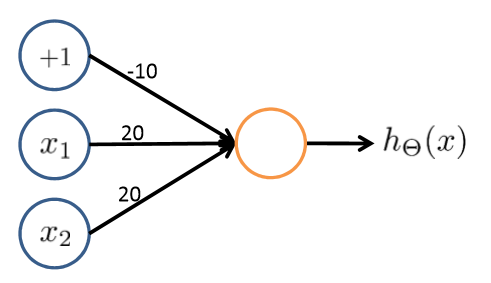
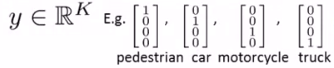
（2）Multi-class classification（多类别分类）：
有K个输出单元
3、代价函数：
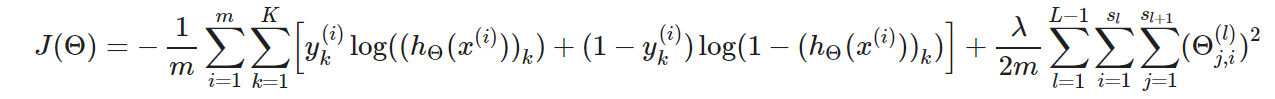
Backpropagation algorithm（反向传播算法）
1、字符定义：
δj(l) ：表示第 l 层的第 j 个结点的误差。
aj(l) : 表示第 l 层的第 j 个结点的激励值。
2、计算过程：（假设是4层神经网络，即下图）【后期推导】
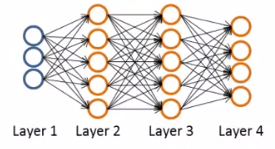
对于第4层的每一个输出单元：
δj(4) = aj(4)- yj （其中 aj(4) 也可记为hθ(x)）
向量化：δ(4) = a(4)- y
δ(3) = (Θ(3))Tδ(4) .*g'(z(3)) ，其中 g'(z(3)) = a(3).*(1-a(3))
δ(2) = (Θ(2))Tδ(3) .*g'(z(2)) ，其中 g'(z(2)) = a(2).*(1-a(2))
δ(1) 不存在误差。
3、算法流程：
（其中向量化表示Δ：
）
通过证明可得【后期推导】：
4、理解算法：
如果 λ = 0，则cost函数为：
接*于*方误差函数。
而δj(l) 是cost函数的偏微分：
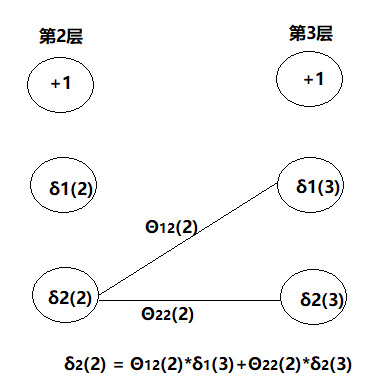
类似于正向传播，反向传播也有：
δj(l) = Θij(l) δi(l+1) + Θi+1 j(l) δi+1(l+1) + Θi+2 j(l) δi+2(l+1)...
例如：
5、算法实现：
（1）简述：
参数：
①先对Θ(1),Θ(2),Θ(3),...进行初始化（跟逻辑回归不一样，这里的 Θ 是矩阵）；
②实现 costFunction 计算 J 和 grad：根据 Θ 正向/反向计算出 D 和 J(Θ)；
③使用 fminunc 函数求出 Θ。
（2）Gradient checking（梯度检测）：
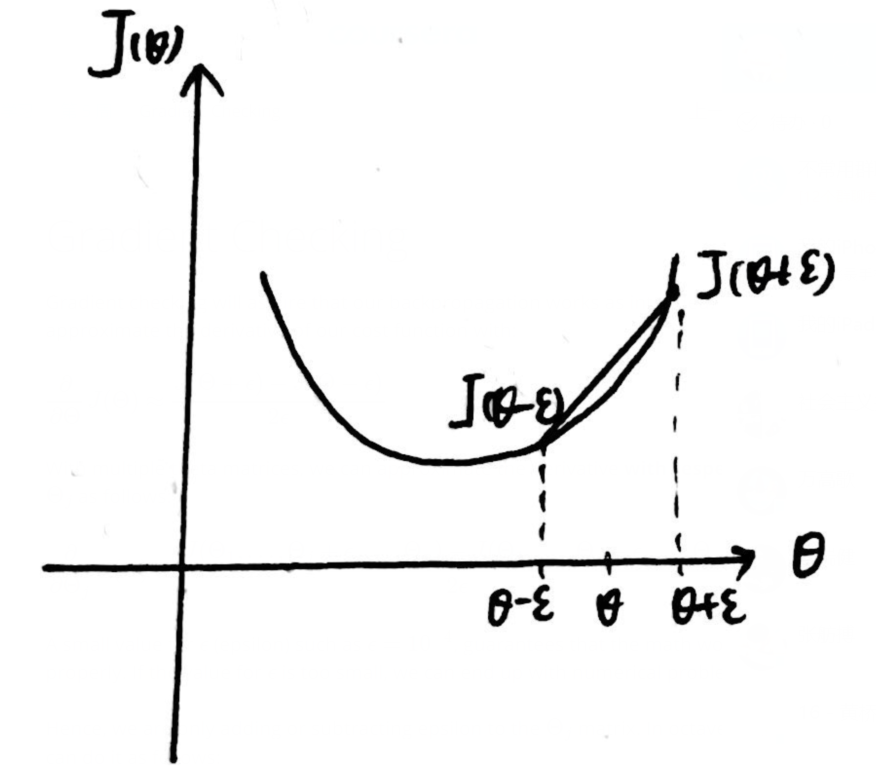
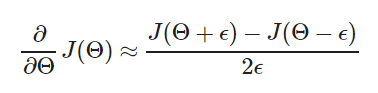一般情况下，ϵ=10−4
对于多个θ，可以具体为：
代码实现：
epsilon = 1e-4;
for i = 1:n,
thetaPlus = theta;
thetaPlus(i) += epsilon;
thetaMinus = theta;
thetaMinus(i) -= epsilon;
gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;
（3） Random initialization（随机初始化）：
不同于逻辑回归，这里的 Θ 初始值不能为全0. 否则会出现每次迭代更新，每一层上的 θ 参数值相等，且每一个 a 的结果也相等，即 a1(2) = a2(2) = ...。
因此初始化时需要打破对称性，将 Θij(l) 设置在[ -ϵ, ϵ ]之间。
代码举例：
If the dimensions of Theta1 is 10x11, Theta2 is 10x11 and Theta3 is 1x11.
Theta1 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta2 = rand(10,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
Theta3 = rand(1,11) * (2 * INIT_EPSILON) - INIT_EPSILON;
神经网络总结
1、选择神经网络：
输入层的神经元数量：根据特征的维度
输出层的神经元数量：根据划分的类别数量
隐藏层的神经元数量：默认多个隐藏层的神经元数量相同，隐藏层的神经元数量稍大于输入特征的数量。
2、训练神经网络：
（1）随机初始化权重；
（2）通过正向传播求 hθ(x(i))
（3）计算代价函数 J(Θ)
（4）通过反向传播求 D（即
）：
compute Δ
end %for
compute D
（5）使用梯度检测比较上述计算结果和用数值方法计算结果是否*似。检测结束后将这部分代码去除，保证代码的执行效率。
（6）使用梯度下降法或者其它优化算法最小化 J(Θ)（比如使用fminunc函数）。
