机器学习笔记（三）逻辑回归
Classification（分类）
1、问题背景：
特殊的样本点会使得分界点发生漂移，影响准确性。
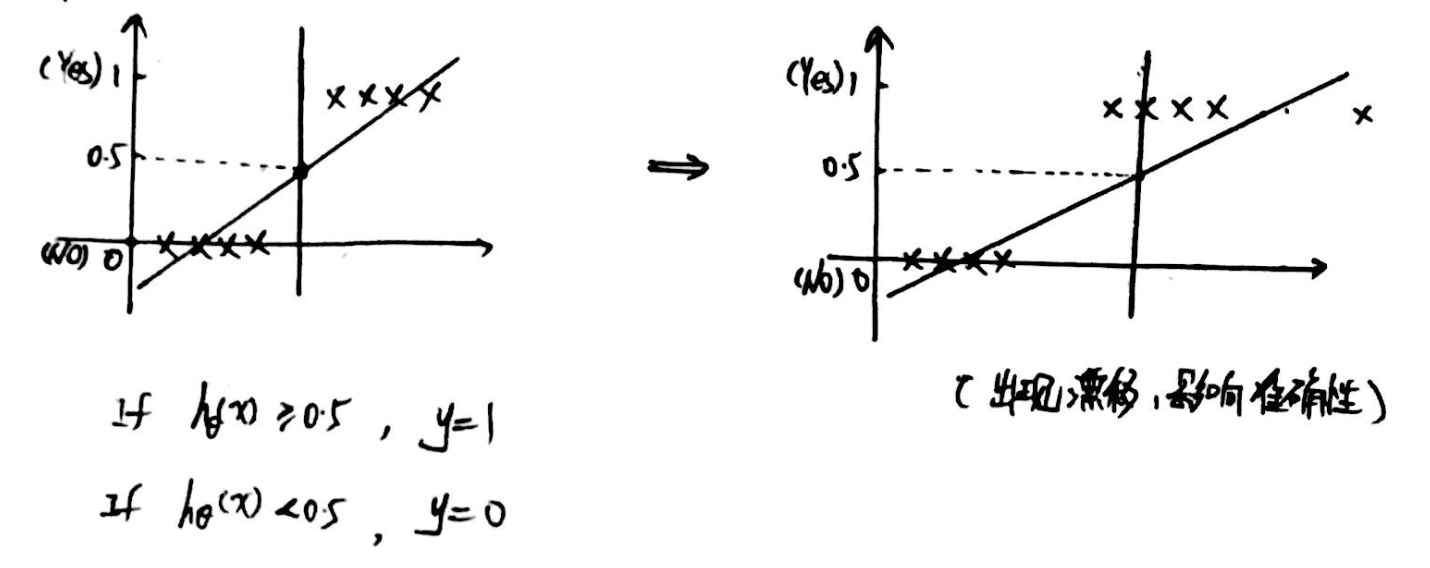
Hypothesis representation（假设函数表达式）
1、Logistic regression Model（逻辑回归模型）：
（1）Sigmoid function / Logistic function S型函数/逻辑函数：
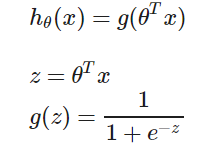
（2）g(z)图像：
（3）hθ(x) 表示在给定参数θ对于某个特征值x的情况下，y=1的概率：
Decision boundary（决策边界）
1、什么是决策边界？
If hθ(x) = g(θTx) ≥ 0.5，则 y = 1 （即 θTx ≥ 0时）；
If hθ(x) = g(θTx)＜ 0.5，则 y = 0（即 θTx＜ 0时）.
举例：对于
，θ=[-3，1，1]T，则
y=1，if -3+x1+x2 ≥ 0，即分界线为 x1+x2 = 3，如下图所示。
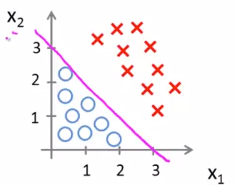
该边界线称为“决策边界”，边界上方部分y=1，下方部分y=0.
2、Non-linear decision boundaries（非线性决策边界）：
例如：
对于θ = [-1，0，0，1，1]T时，决策边界为x1² + x2² = 1，如下图所示。
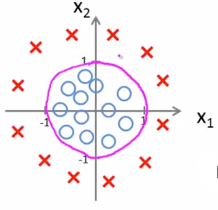
Cost function（代价函数）
1、数据量化：
训练集：
m个训练样本（每个样本含有n个特征值）：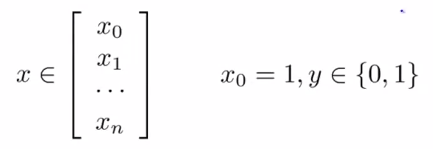
假设函数：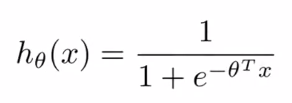
2、Logistic regression cost function（逻辑回归代价函数）：
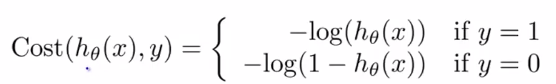
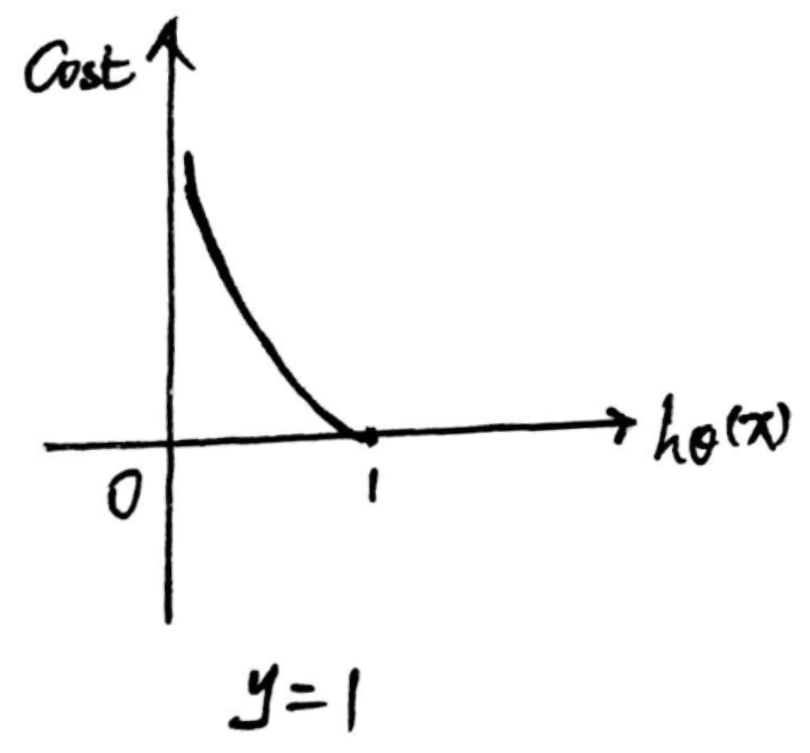
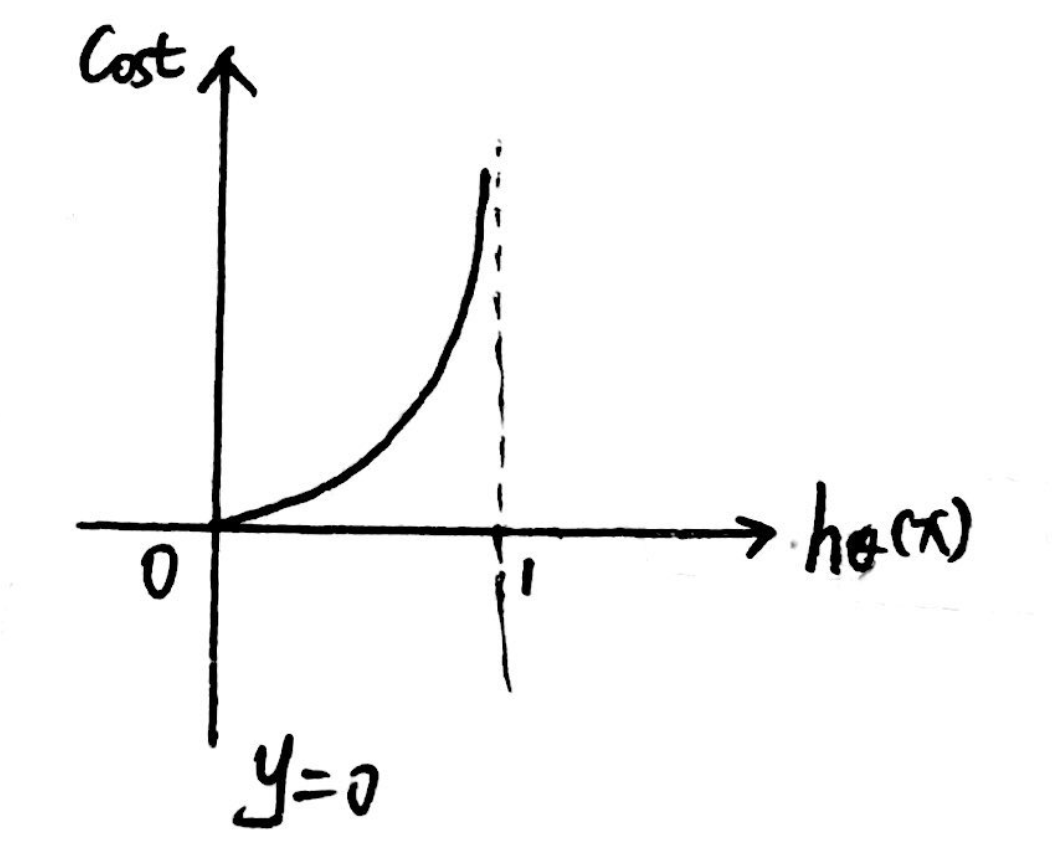
【理解】
当y = 1时，真实值为1，当预测值越靠近1，则代价越小；
当y = 0时，真实值为0，当预测值越靠近0，则代价越小。
3、Simplified cost function（简化代价函数）：
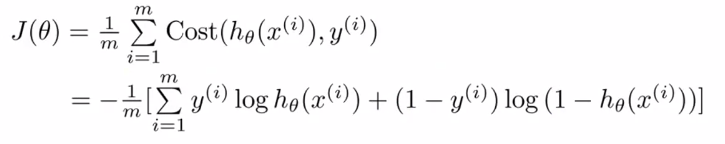
Gradient Descent（梯度下降法）
1、算法流程：
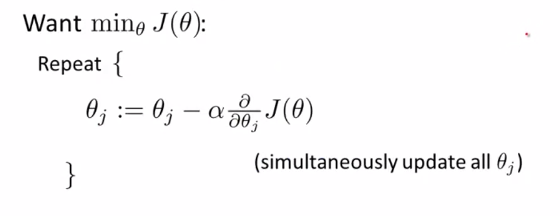
即：
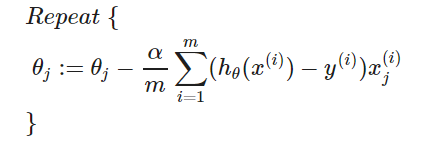
【推导】碰巧跟线性回归的算法一致？
为了推导的方便，对于公式进行了适当简写：
2、向量化表示：
优化算法
1、算法概览（暂时仅了解）：
Conjugate gradient（共轭梯度法）
BFGS（变尺度法）
L-BFGS（限制变尺度法）
优点：不需要设置α；比梯度下降更快
缺点：更复杂
2、Matlab调用方式 ：
（1）编写costFunction(theta)函数：
（2）设置参数，调用fminunc()函数：
Multiclass Classification（多类别分类）
1、策略思想：
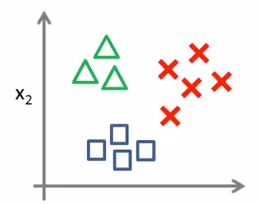
将除第1种外的分类合并，看做同一个分类进行处理，依次识别出3种分类。
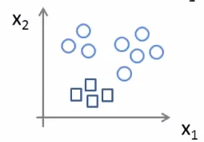
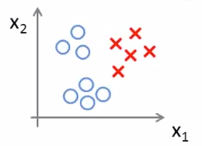
2、算法描述：
对于每一个分类i都进行 y = i 情况下逻辑回归模型
的计算，对于每一个新输入的x进行预测，挑选出使得预测值最大的i，即
.
Regularization（正规化）
1、Overfitting（过度拟合）：
存在过多的变量，把训练集拟合得很好，代价函数接近0，但是不能推广至新的样本。
线性回归举例：下图1为underfit（欠拟合），下图3位overfit（过度拟合）
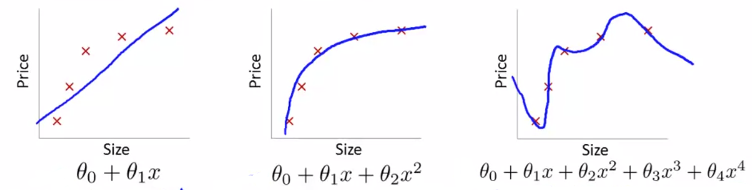
逻辑回归举例：下图1为underfit（欠拟合），下图3位overfit（过度拟合）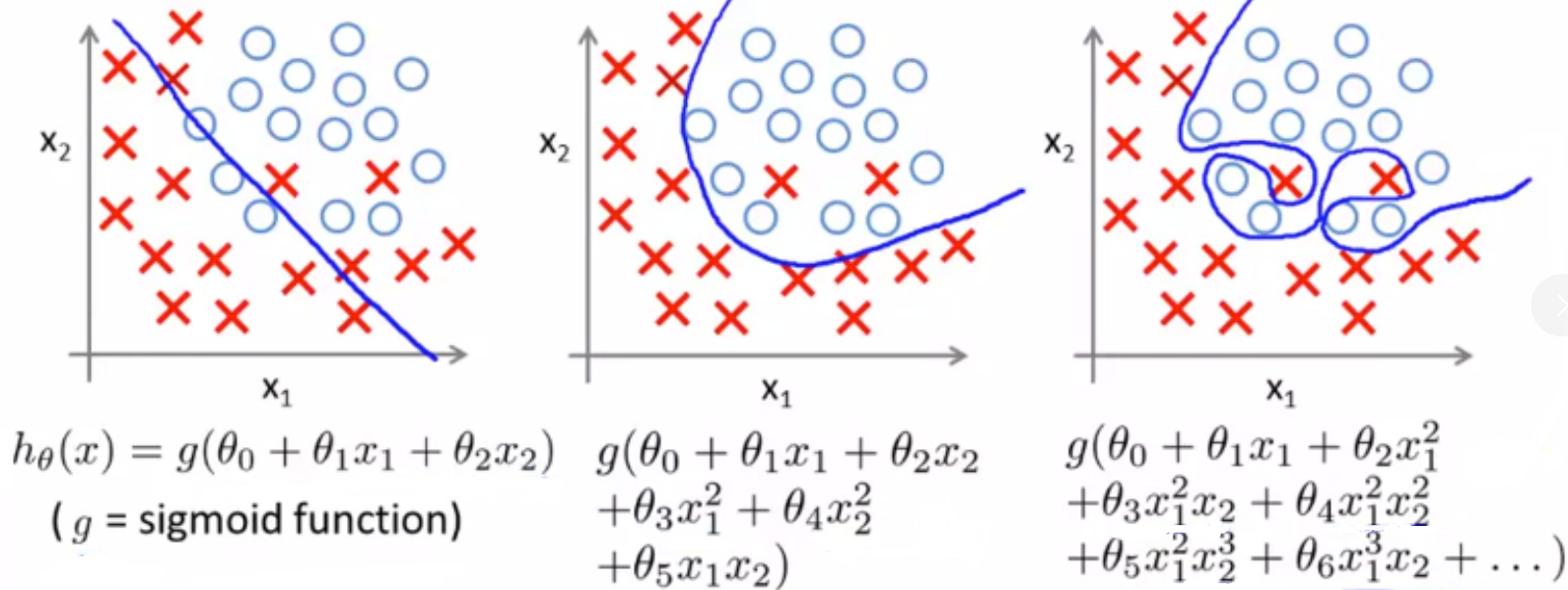
2、过度拟合的解决方法：
（1）降低特征的数量：人工筛选特征，模型选择算法（暂不深入）；
（2）正则化：保留所有特征但降低参数θ的大小，存在大量特征但每个特征对于预测结果仅产生较小的影响。
3、Regularized Linear Regression（正则化线性回归）：
（1）代价函数：
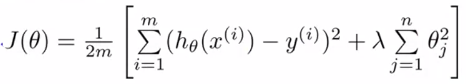（注：θ从1开始）
添加的项称为“正则化项”，λ称为“正则化参数”。
如果λ太大，则会欠拟合（接近一条水平直线）
（2）梯度下降算法：
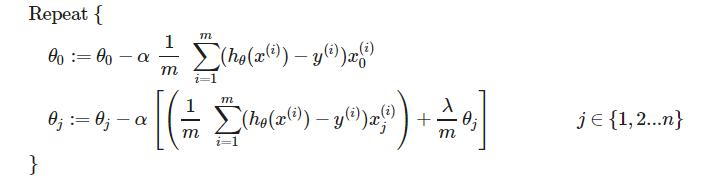
下式可改写为：
其中
小于1，将θj进行了一定的压缩。
（3）Normal equation（正规方程）：
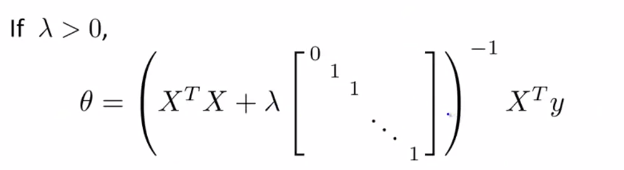
4、Regularized logistic regression（正则化逻辑回归）：
（1）代价函数
（2）梯度下降算法：同正则化线性回归的梯度下降算法，但假设函数不同。
