机器学习笔记(二)多元线性回归
Multiple Features (多特征量)
1、字符定义:

2、Multivariate Linear Regression (多元线性回归):

3、代价函数:
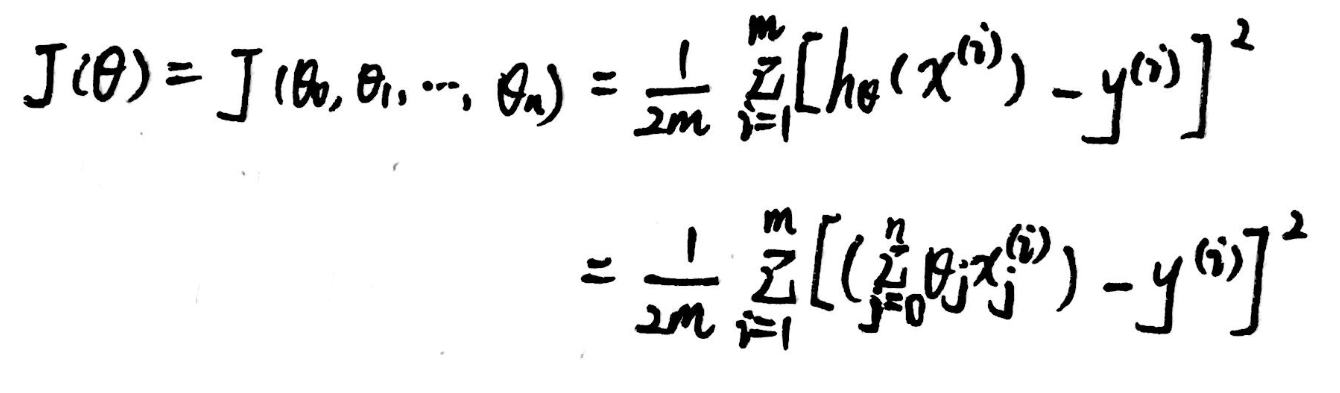
4、梯度下降算法:
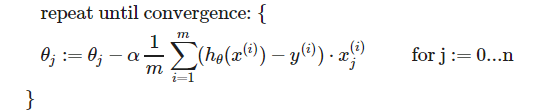
梯度下降技巧一——Feature Scaling (特征缩放)
1、定义:将每个特征量缩放到-1和1之间。(与之范围接近即可,如0~3,-2~0.5等)
2、作用:方便梯度下降时的收敛(轮廓图更接近圆)。
3、缩放方法:
(1)直接除以最大值。
(2)Mean Normalization(均值归一化):减去平均值再除以s(即最大值-最小值,也可以是标准差)
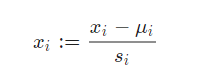
梯度下降技巧二——Learning Rate (学习速率)
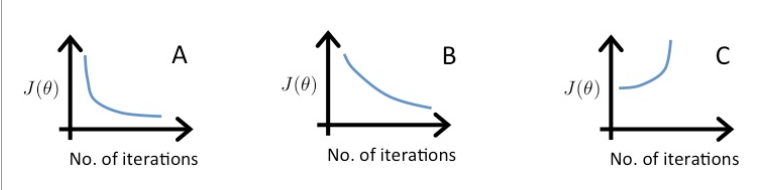
A:α=0.1 B:α=0.01(α较小,收敛速度慢) C:α=1(α太大,发散)
Polynomial Regression (多项式回归)
1、举例:不同次项可以转换为不同的特征值,如面积为特征值x1,面积²为特征值x2,面积³为特征值x3。将多项式回归问题转化为多元线性回归问题。
![]()
Normal Equation (正规方程)
1、作用:一步求解最优值。不需要进行特征归一化处理。(适用于n较小的情况)
2、矩阵表示:
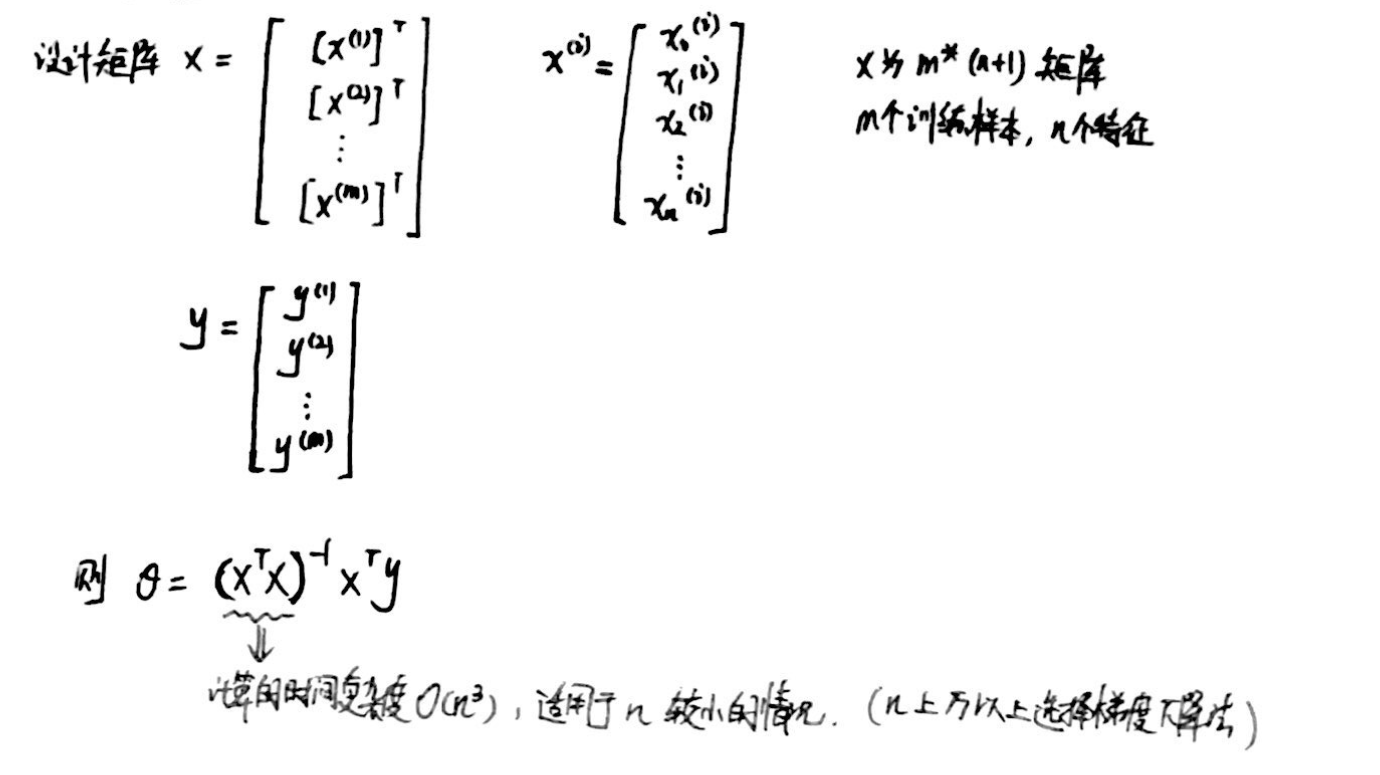
3、推导过程:参考博客
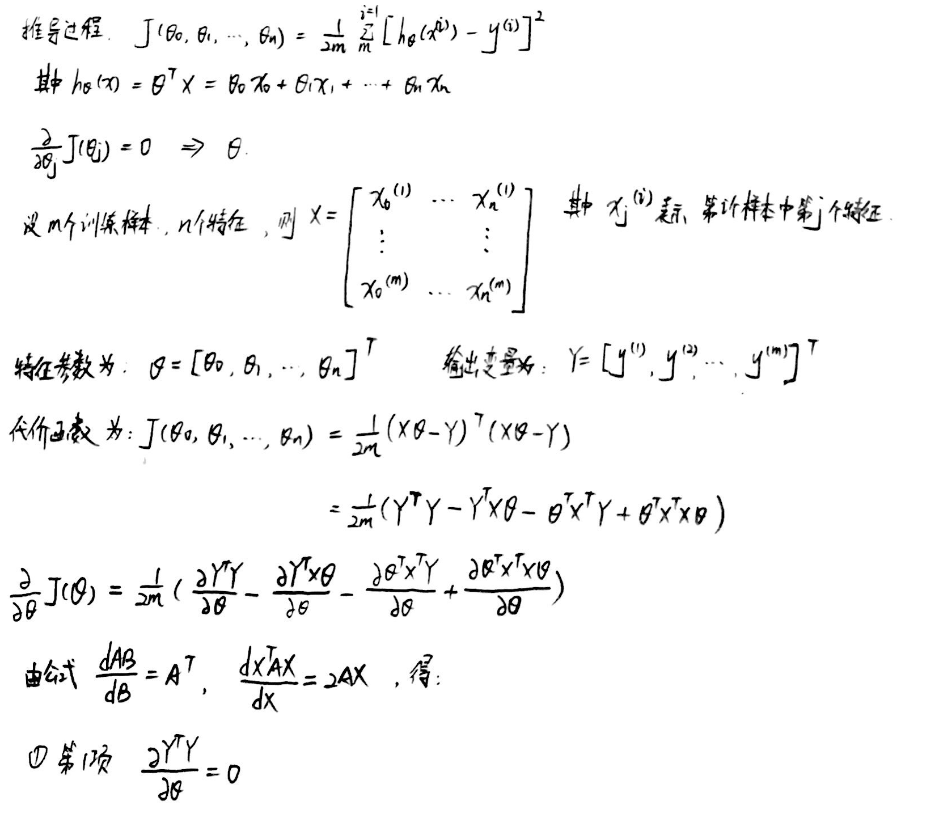


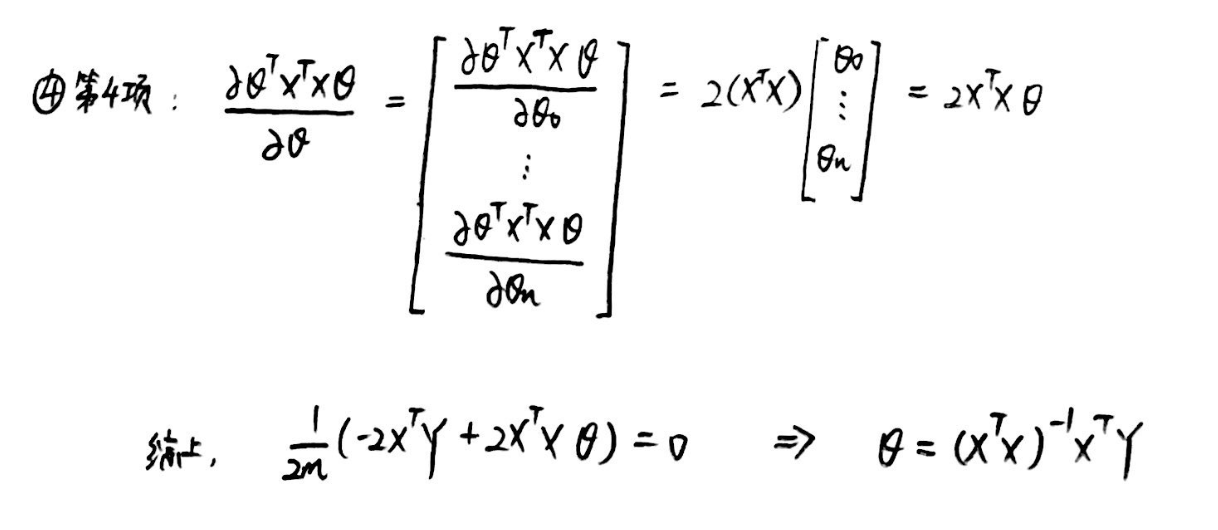
4、 XTX不可逆的情况:
两种可能性:(1)一种是特征选的很多余了(即两个特征相关),比如选了房子的平方面积作为特征还选了房子的英尺计算的面积;(2)一种是特征选的太多(即m≤n),比如你有10个样本,结果选了1000个特征。



