【题解】第36次CCF-CSP认证

合集 - MyAlgorithmStudy(13)

1.PTA 函数与递归部分题目讲解及思路2023-10-18 2.高精度加减乘除2023-10-18 3.PTA数组及排序查找题解与解题思路2023-10-28 4.Educational Codeforces Round 160 (Rated for Div. 2) 题解A~D2023-12-19 5.Codeforces Round 916 (Div. 3) (A~F附带题解和详细思路)2023-12-20 6.CEIT算法训练-双指针部分题解(全12题)2024-01-31 7.【题解】2023传智杯全国大学生程序设计竞赛-初赛第一场2024-10-10 8.2024 秋季PAT认证甲级(题解A1-A4)2024-09-03 9.处理若干行输入的题目2024-10-14 10.【题解】CEIT 2024 第三周算法训练讲义题解2024-10-14 11.2024 CCPC第五届辽宁省程序设计竞赛集训12024-10-20 12.2024 CCPC第五届辽宁省程序设计竞赛集训22024-10-24

13.【题解】第36次CCF-CSP认证2024-12-09

UPDATE

update(2024/12/10) : 修正了E题代码的小错误，十分感谢 @Andyqian7 提供的hack数据！
update(2024/12/15) : 修正了B题题解中存在问题的表述，十分感谢 @iy88 指出这个问题！

概述

本次重现赛已经上传到SYNU OJ,本校的同学可以去对应的页面补题。

	A. 移动	B. 梦境巡查	C. 缓存模拟	D. 跳房子	E. 梦魇
题目参考难度	800	1400	2000	2100	3500
涉及知识点	模拟	前缀和，枚举	数据结构	记忆化搜索，bfs	深度优先搜索，笛卡尔树，单调栈

题解报告

A. 移动

直接模拟即可。

int main()
{
    cin.tie(0)->sync_with_stdio(0);
    cout.tie(0);
    int n, k;
    cin >> n >> k;
    while (k--)
    {
        int x, y;
        cin >> x >> y;
        string op;
        cin >> op;
        for (int i = 0; i < op.size(); i++)
        {
            int tx = x, ty = y;
            if (op[i] == 'f')
                ty++;
            else if (op[i] == 'b')
                ty--;
            else if (op[i] == 'l')
                tx--;
            else
                tx++;

            if (tx >= 1 and tx <= n and ty >= 1 and ty <= n)
            {
                x = tx, y = ty;
            }
        }
        cout << x << ' ' << y << '\n';
    }
}

B. 梦境巡查

update(2024/12/15) :实际上，我这里表示的 $a_{i}$ 实际上应该表示的是题意中的 $a_{i - 1}$ ，这是因为我在题目中处理输入的时候自动将 $a_{i}$ 向后偏移了一位，也就是代码 for(int i = 1; i <= n + 1; i ++) cin >> a[i]; 的部分，原始的输入应该是 $a_{0} \sim a_{n}$ ，而我将他处理成了 $a_{1} \sim a_{n + 1}$ 。但是，最后的代码的正确性并不会受到影响。请将下文中的 $a_{i}$ 当成题意中的 $a_{i - 1}$ 即可！

首先，不考虑题目中对于 $b_{i}$ 的修改，如何求出最开始的 $w$ 呢？假设，我们记 $f (x)$ 表示到达 $x$ 点时，还未补给 $b_{i}$ 时当前的能量值(可以为负数)，同时，我们记点 $n + 1$ 表示最后回到 $0$ 点，那么 $f (x)$ 的递推式就很明显了，即：

f (x) = {\begin{matrix} f (x - 1) - a_{i} + b_{i - 1} (x > 1) \\ 0 (x = 1) \end{matrix}

虽然我们求出的 $f (x)$ 存在负数，而这是一种非法的状态，而我们实际上就是要将所有非法的状态合法化。那么，我们假设最开始的 $w$ ，上述公式变成：

f (x) = {\begin{matrix} f (x - 1) - a_{i} + b_{i - 1} (x > 1) \\ w (x = 1) \end{matrix}

这一步表示，我给之后的 $f (x)$ 都加上一个 $w$ ，那么，要合法化所有的 $f (i)$ 并且最小化 $w$ ，只需要让 $w$ 取得所有 $f (i)$ 的最小值的相反数即可。

w = - {min}_{i = 1}^{n + 1} (f (i))

上述是不带修改的 $w$ 的求解方法，那么考虑带修如何操作？假设当前点记为 $p$ ，我现在要修改 $b_{p} \leftarrow 0$ ，会产生什么影响呢？实际上，根据上述公式，它会影响到 $f (p + 1)$ 到 $f (n + 1)$ 的所有值，让他们全部都减少 $b_{p}$ ，而此时，根据 $w$ 的计算公式，在 $f (p + 1)$ 到 $f (n + 1)$ 之间，可能会产生新的更小值，所以

w (p) = min (w, {min}_{i = p + 1}^{n + 1} (f (i)) - b_{p})

通过上述公式，我们发现， ${min}_{i = p + 1}^{n + 1} (f (i))$ 实际上就是 $f (i)$ 的后缀最小值，因此我们只需要预处理出来即可。每次计算 $w (p)$ 都是 $O (1)$ 的，总复杂度是 $O (n)$ 。

int main()
{
    cin.tie(0)->sync_with_stdio(0);
    cout.tie(0);
    int n;
    cin >> n;
    vector<int> a(n + 2), b(n + 1), f(n + 2);
    for(int i = 1; i <= n + 1; i ++) cin >> a[i];
    for(int i = 1; i <= n; i ++) cin >> b[i];
    int w = 0;
    for(int i = 1; i <= n + 1; i ++)
    {
        f[i] = f[i-1] - a[i] + b[i-1];
        w = min(w, f[i]);
    }
    vector<int> sufmin(n + 3, 1e9);
    for(int i = n + 1; i >= 1; i --)
    {
        sufmin[i] = min(sufmin[i + 1], f[i]);
    }
    for(int i = 1; i <= n; i ++)
    {
        cout << -min(w, sufmin[i + 1] - b[i]) << ' ';
    }
}

C. 模拟缓存

大模拟，实际上先把流程图画出来会好很多，这样就知道什么时候该记录答案了。

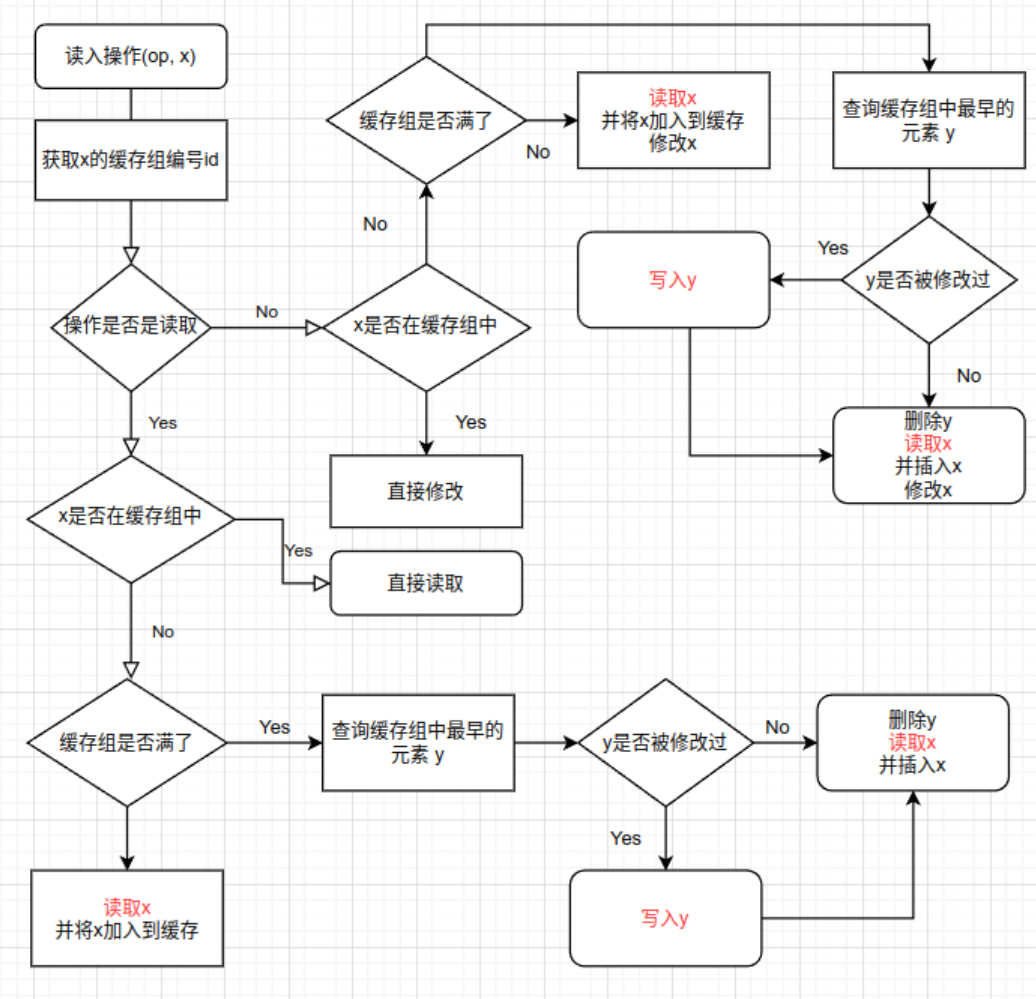
图片中标红的部分就是应该记录答案的地方。

实际上我们只需要考虑实现上述过程中的部分瓶颈操作即可。

如何记录操作的先后顺序：可以对每次操作都记录一个时间戳，再用一个set维护pair即可，pair第一维存时间戳，第二维存 $x$ 。由于set存储是有序的，因此时间戳应该倒序赋值，这样在set中，时间戳小的排在前面，表示发生时间距离当前最近。
查询是否在缓存中：可以采用set的lower_bound，每次查询 $x$ 是否在缓存中，可以查询 $x$ 最近的时间戳，这样即可快速判断，并且直接获取到 $x$ 的迭代器。
删除距离当前时间最久的缓存内容：可以采用set的rbegin()，这样每次删除最久远的元素即可。
验证缓存中的 $x$ 是否被修改过，可以使用一个 map 来作为标记数组。

注意事项：

每次别忘记操作完 $x$ 之后，要及时更新 $x$ 的时间戳(尤其是set中的时间戳)。
每次修改时记得打上修改标记，同时如果被修改过的数要被删除了，记得去掉它的标记。
如果缓存满了要删除某个元素，同时要写入内存，记住记录答案时写入操作的顺序在读入前面。

using i64 = long long;
using pii = pair<int, int>;

signed main()
{
    cin.tie(0)->sync_with_stdio(0);
    cout.tie(0);
    int n, N, q;
    cin >> n >> N >> q;
    // n 组大小 N 组数
    auto getid = [&](int x)
    {
        return x / n % N;
    };
    vector<set<pii>> group(N); // 缓存组
    vector<pii> ans;
    map<int, int> ismodify; // 是否被修改
    int idx = 0;
    map<int, int> timestamp; // 时间戳
    while(q--)
    {
        int op, a;
        cin >> op >> a;
        if(op == 0) 
        {
            int id = getid(a);
            auto it = group[id].lower_bound({timestamp[a], 0});
            if(it != group[id].end() and it -> second == a) // 如果a已经在缓存中
            {
                // 更新时间戳
                group[id].erase(it);
                group[id].insert({q, a});
            }
            else // 不在缓存中
            {
                // 缓存组未满
                if(group[id].size() < n)
                {
                    // 直接读入内存
                    ans.push_back({0, a});
                    group[id].insert({q, a});
                }
                // 缓存组满了
                else
                {
                    // 找到最后一个没有被修改的，也即是被替换的
                    auto tmp = group[id].rbegin() -> second;
                    // 如果他在缓存中被修改过
                    if(ismodify[tmp]) 
                    {
                        // 先同步修改到内存
                        ans.push_back({1, tmp});
                        // 去掉修改标记
                        ismodify[tmp] = 0;
                    }
                    group[id].erase(group[id].lower_bound({timestamp[tmp], tmp}));
                    // 再读入新的数据进来
                    group[id].insert({q, a});
                    ans.push_back({0, a});
                }
            }
        }
        else
        {
            int id = getid(a);
            auto it = group[id].lower_bound({timestamp[a], 0});
            if(it != group[id].end() and it -> second == a) // 如果a已经在缓存中
            {
                // 更新时间戳
                // 直接修改，并将它标记成已修改
                group[id].erase(it);
                group[id].insert({q, a});
                ismodify[a] = 1;
            }
            else
            {
                // 缓存组未满, 先读入，再修改
                if(group[id].size() < n)
                {
                    // 直接读入内存
                    ans.push_back({0, a});
                    group[id].insert({q, a});
                    ismodify[a] = 1;
                }
                else 
                {
                    // 找到最后一个没有被修改的，也即是被替换的
                    auto tmp = group[id].rbegin() -> second;
                    // 如果他在缓存中被修改过
                    if(ismodify[tmp]) 
                    {
                        // 先同步修改到内存
                        ans.push_back({1, tmp});
                        // 去掉修改标记
                        ismodify[tmp] = 0;
                    }
                    group[id].erase(group[id].lower_bound({timestamp[tmp], tmp}));
                    // 再读入新的数据进来
                    group[id].insert({q, a});
                    ans.push_back({0, a});
                    ismodify[a] = 1;
                }
            }
        }
        timestamp[a] = q;
    }
    // cout << "------------" << '\n';
    for(auto [x, y] : ans)
    {
        cout << x << ' ' << y << '\n';
    }
}

D. 跳房子

看上去是一个 $O (n)$ 的bfs, 但是在建图的时候，复杂度就 $O (n^{2})$ 了。考虑如何优化：我们主要需要解决一个点会被多个点搜到，这样会产生极高的复杂度。实际上，我们可以使用一个set容器，每次搜索的时候，如果已经搜到了的点，就直接暴力erase掉。这样每个点只会被搜到一次，复杂度就变成了 $O (n \log n)$ 。

实际上本题还有更优秀的做法，只需要在搜索过程中维护一个 $m a x_{R}$ ，表示可达右边界，每次搜索只从 $m a x_{R}$ 开始搜，每次更新 $m a x_{R}$ ，由于 $m a x_{R}$ 是单调的，因此这样的复杂度是 $O (n)$ 的，可以自行实现。

int main()
{
    cin.tie(0)->sync_with_stdio(0);
    cout.tie(0);
    int n;
    cin >> n;
    vector<int> a(n + 1), k(n + 1), vis(n + 1);
    for(int i = 1; i <= n; i ++)
        cin >> a[i];
    for(int i = 1; i <= n; i ++)
        cin >> k[i];
    queue<int> q;
    q.push(1);
    vis[1] = 1;
    set<int> unvis_pos;
    for(int i = 2; i <= n; i ++) unvis_pos.insert(i);
    int dist = 0;
    while(q.size())
    {
        int T = q.size();
        dist ++;
        while(T--)
        {
            auto u = q.front();
            q.pop();
            if(u + k[u] >= n) 
            {
                cout << dist << '\n';
                return 0;
            }
            auto it = unvis_pos.lower_bound(u + 1);
            vector<int> del;
            for(;*it <= u + k[u] and it != unvis_pos.end(); it++)
            {
                del.push_back(*it);
                // cout << *it << '\n';
                if(!vis[*it - a[*it]])
                {
                    // cout << *it - a[*it] << '\n';
                    vis[*it - a[*it]] = 1;
                    q.push(*it - a[*it]);
                }
            }
            for(int i : del) unvis_pos.erase(i);
        }
    }
    cout << -1 << '\n';
}

E. 梦魇

本题解法是群友Bezime提供的，特别鸣谢！Orz

单调栈建立笛卡尔树，维护maxl和maxr。答案就是 $min (f [i] [0], f [i + 1] [0])$ ，更加详细的做法看代码注释。

update(2024/12/10) : 将代码单调栈从后往前扫的部分的 while (qt && q[qt] <= a[i]) 改为 while (qt && q[qt] < a[i])

using i64 = long long;
const int N = 5e6 + 5;

inline void qread(i64 &x)
{
    x = 0;
    short f = 1;
    char c = getchar();
    while ((c < '0' || c > '9') && c != '-')
        c = getchar();
    if (c == '-')
        f = -1, c = getchar();
    while (c >= '0' && c <= '9')
        x = x * 10 + c - '0', c = getchar();
    x *= f;
}
inline void qwrite(i64 x)
{
    if (x < 0)
        putchar('-'), x = -x;
    if (x > 9)
        qwrite(x / 10);
    putchar(x % 10 + '0');
}

i64 T = 1, n, t, k, ans;
i64 a[N], b[N], c[N], d[N];
i64 sum[N], mxl[N], mxr[N];
i64 q[N], o[N], qt;
i64 mx;
i64 f[N][3];

void dfs(i64 x)
{
    i64 xl = mxl[x], xr = mxr[x];
    // 如果左边的那个f的3个值没有定下来，求值
    if (!f[xl][0])
        dfs(xl); 
    // 如果右边的那个f的3个值没有定下来，求值
    if (!f[xr][0])
        dfs(xr);                                                                        
    // 这些是关于xl,x,xr的整段（xl+1~xr-1）、左段（xl+1~x-1）、右段（x+1~xr-1）区间和
    i64 w = sum[xr - 1] - sum[xl], wl = sum[x] - sum[xl], wr = sum[xr - 1] - sum[x - 1];
    // 后面操作不拿这一整段的最小起始攻击力
    //（如果xl<=xr，那么f[xl][1]<=f[xr][2]，而mxr[xl]应恰好等于xr，故f[xl][1]恰好跳过了xl+1~xr-1）。
    // 这一整段都没拿过，因此求f的3个值时可以随意加上区间内b的值
    i64 mn = min(f[xl][1], f[xr][2]);
    // 第一步自身起手，至少带a[x]的攻击力，拿走整段的b值
    f[x][0] = max(a[x], mn - w); 
    // 拿走左段的b值，留下右段的b值不拿，用来求右段的f的3个值
    f[x][1] = max(a[x], mn - wl);
    // 拿走右段的b值，留下左段的b值不拿，用来求左段的f的3个值
    f[x][2] = max(a[x], mn - wr);
}
void solve()
{
    qread(n);
    for (i64 i = 1; i <= n; i++)
        qread(c[i]);
    for (i64 i = 1; i <= n; i++)
        qread(d[i]);
    qread(t);
    while (t--)
    {
        for (i64 i = 1; i <= n; i++)
            a[i] = c[i], b[i] = d[i], f[i][0] = 0;
        qread(k);
        while (k--)
        {
            i64 x, l, r;
            qread(x), qread(l), qread(r);
            a[x] = l, b[x] = r;
        }
        qt = ans = mx = 0;
        for (i64 i = 1; i <= n; i++)
        {
            // b的前缀和
            sum[i] = sum[i - 1] + b[i]; 
            // 记录最大a值，f的值不可能大于它
            mx = max(mx, a[i]);
            while (qt && q[qt] <= a[i])
                qt--;
            // 左边第一个大于
            mxl[i] = o[qt]; 
            q[++qt] = a[i], o[qt] = i;
        }
        // 给边界一个初值
        f[0][0] = f[0][1] = f[0][2] = f[n + 1][0] = f[n + 1][1] = f[n + 1][2] = mx; 
        qt = 0, o[0] = n + 1; // n+1是右边界
        for (i64 i = n; i; i--)
        {
            while (qt && q[qt] < a[i]) // update: 这里原来的 <= 改为 <
                qt--;
            mxr[i] = o[qt]; // 右边第一个大于等于
            q[++qt] = a[i], o[qt] = i;
        }
        for (i64 i = 1; i <= n; i++)
            if (!f[i][0])
                dfs(i); // 如果f值还没有定下来，求值
        for (i64 i = 1; i < n; i++)
            ans ^= min(f[i][0], f[i + 1][0]);
        qwrite(ans), puts("");
    }
}
int main()
{
    while (T--)
        solve();
}

posted @ 2024-12-09 14:46 橙之夏阅读(2636) 评论(7) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· CEIT算法训练-双指针部分题解(全12题)

· 2024 CCPC第五届辽宁省程序设计竞赛集训2

· 第36次 CCF CSP 计算机软件能力认证题解（民间版）

· 可达暑期集训笔记：CSP-S 沃思班

· 暑假集训CSP提高模拟26

阅读排行：
· 《HelloGitHub》第 108 期
· Windows桌面应用自动更新解决方案SharpUpdater5发布
· 我的家庭实验室服务器集群硬件清单
· C# 13 中的新增功能实操
· Supergateway：MCP服务器的远程调试与集成工具

公告

昵称：橙之夏
园龄： 1年5个月
粉丝： 10
关注： 1

+加关注

2025年3月

日

一

二

三

四

五

六

OrangeCodeLog

Hello, Algorithm!

【题解】第36次CCF-CSP认证

UPDATE

概述

题解报告

A. 移动

B. 梦境巡查

C. 模拟缓存

D. 跳房子

E. 梦魇

公告

搜索

常用链接

我的标签

合集

随笔档案

阅读排行榜

评论排行榜

推荐排行榜

最新评论