固体物理复习(一)晶体结构描述和布拉格定律

预备知识

1.晶胞

Crystal structure = Lattice(点阵) * Basis(基元)

以NaCl为例, NaCl晶体的点阵为面心立方结构, 其基元包含一个Na和一个Cl.

三维点阵的类型:
Triclinic: a₁!=a₂!=a₃, θ₁!=θ₂!=θ₃ ,修饰 P
Monoclinic:  a₁!=a₂!=a_3, θ₁=θ₂=90°!=θ₃,P,C
Orthorhombic: a₁!=a₂!=a₃,  θ₁=θ₂=θ₃=90°,P,I,F,C 
Tetragonal: a₁=a₂!=a_3, θ₁=θ₂=θ₃=90°,P,I
Cubic: a₁=a₂=a₃,  θ₁=θ₂=θ₃=90°,P,I,F
Trigonal: a₁=a₂=a₃,  θ₁=θ₂=θ₃<120°, !=90°,P
Hexagonal: a₁=a₂!=a_3, θ₁=θ₂=90°, θ₃=120°,P

P=原胞(1个点阵点), I=体心(2点阵点), F=面心(4点阵点), C=Side-centred, 即在顶面和底面添加点阵点

4种修饰*7种晶格系统组合起来得到14种Bravais点阵 

2. 对称操作

平移对称操作: T=u₁a₁+u₂a₂+u₃a₃, u₁u₂u₃为整数,  a₁a₂a₃为基矢

     基矢 a₁a₂a₃ = 晶格常数 a₁a₂a₃

点对称操作: 对应群论的点群操作

3. 原胞

原胞(primitive cell):点阵中的最小晶胞, 一个点阵点对应一个原胞.

wigner-seitz胞:划分原胞的一种方式, 取点间连线的中垂线围成的最小面积.

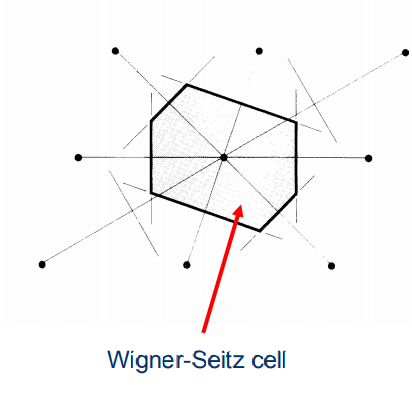(wigner-seitz胞示意图)

正格子与倒格子

1.正格子

正格子中的布拉格定律:

2dsinθ=nλ

2.倒格子

由于正格子的布拉格理论无法描述散射的强度, 因此要对正格子进行傅里叶变化

首先将一维电子浓度n(r)进行傅里叶展开

n(r)=n₀+Σ(C_pcosθ+S_psinθ)

     =Σn_pexp(iθ), 令-n_p=n_p*使n(r)为实数

θ=2πpx/a

由此引出倒格子的概念, 2πp/a为晶体倒格子, 或在傅里叶空间中的一个点.

推广到三维有

n(r)=Σn_Gexp(iG*r)

G=v₁b₁+v₂b₂+v₃b₃,

b₁=2π·a₂xa₃/(a₁·a₂xa₃), b₂=2π·a₃xa₁/(a₁·a₂xa₃),b₃=2π·a₁xa₂/(a₁·a₂xa₃)

倒格子空间中的Wigner-Seitz胞称为布里渊区, 布里渊区在晶体电子能带理论中有重要地位

接下来推导倒格子的布拉格定律:

首先引入散射振幅F的定义

F=∫dVn(r)exp(-iΔk·r)

Δk为散射波与入射波的波矢差k'-k

将n(r)傅里叶展开

F=∫dVΣn_Gexp(iG*r)exp(-iΔk·r)

  =Σ∫dVn_Gexp(i(G-Δk)·r)

由此可以看出, 当Δk=G时F=Vn_G, 发生弹性散射.

发生弹性散射时, 光子能量E=ћω守恒, ω=ck, 因此入射波波矢大小与散射波波矢相等, 即k²=k'²

因为k+G=k', 所以综上有(k+G)²=k'²

即2k·G=G², 此即倒格子空间的布拉格定律的形式.