最短路径——Floyd-Warshall算法
Floyd-Warshall算法,简称Floyd算法,用于求解任意两点间的最短距离,时间复杂度为O(n^3)。
我们平时所见的Floyd算法的一般形式如下:
1 void Floyd() 2 { 3 int i,j,k; 4 for(k=1;k<=n;k++) 5 for(i=1;i<=n;i++) 6 for(j=1;j<=n;j++) 7 if(dist[i][k]+dist[k][j]<dist[i][j]) 8 dist[i][j]=dist[i][k]+dist[k][j]; 9 }
注意下第6行这个地方,如果dist[i][k]或者dist[k][j]不存在,程序中用一个很大的数代替。最好写成if(dist[i][k]!=INF && dist[k][j]!=INF && dist[i][k]+dist[k][j]<dist[i][j]),从而防止溢出所造成的错误。
上面这个形式的算法其实是Floyd算法的精简版,而真正的Floyd算法是一种基于DP(Dynamic Programming)的最短路径算法。
例题分析:
设图G中n 个顶点的编号为1到n。令c [i, j, k]表示从i 到j 的最短路径的长度,其中k 表示该路径中的最大顶点,也就是说c[i,j,k]这条最短路径所通过的中间顶点最大不超过k。因此,如果G中包含边<i, j>,则c[i, j, 0] =边<i, j> 的长度;若i= j ,则c[i,j,0]=0;如果G中不包含边<i, j>,则c (i, j, 0)= +∞。c[i, j, n] 则是从i 到j 的最短路径的长度。 对于任意的k>0,通过分析可以得到:中间顶点不超过k 的i 到j 的最短路径有两种可能:该路径含或不含中间顶点k。若不含,则该路径长度应为c[i, j, k-1],否则长度为 c[i, k, k-1] +c [k, j, k-1]。c[i, j, k]可取两者中的最小值。 状态转移方程:c[i, j, k]=min{c[i, j, k-1], c [i, k, k-1]+c [k, j, k-1]},k>0。 这样,问题便具有了最优子结构性质,可以用动态规划方法来求解。
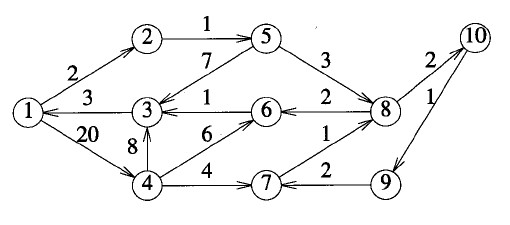
为了进一步理解,观察上面这个有向图:若k=0, 1, 2, 3,则c[1,3,k]= +∞;c[1,3,4]= 28;若k = 5, 6, 7,则c [1,3,k] = 10;若k=8, 9, 10,则c[1,3,k] = 9。因此1到3的最短路径长度为9。 下面通过程序来分析这一DP过程,对应上面给出的有向图:
1 #include <iostream> 2 using namespace std; 3 4 const int INF = 100000; 5 int n=10,map[11][11],dist[11][11][11]; 6 void init() 7 { 8 int i,j; 9 for(i=1;i<=n;i++) 10 for(j=1;j<=n;j++) 11 map[i][j]=(i==j)?0:INF; 12 map[1][2]=2,map[1][4]=20,map[2][5]=1; 13 map[3][1]=3,map[4][3]=8,map[4][6]=6; 14 map[4][7]=4,map[5][3]=7,map[5][8]=3; 15 map[6][3]=1,map[7][8]=1,map[8][6]=2; 16 map[8][10]=2,map[9][7]=2,map[10][9]=1; 17 } 18 void floyd_dp() 19 { 20 int i,j,k; 21 for(i=1;i<=n;i++) 22 for(j=1;j<=n;j++) 23 dist[i][j][0]=map[i][j]; 24 for(k=1;k<=n;k++) 25 for(i=1;i<=n;i++) 26 for(j=1;j<=n;j++){ 27 dist[i][j][k]=dist[i][j][k-1]; 28 if(dist[i][k][k-1]+dist[k][j][k-1]<dist[i][j][k]) 29 dist[i][j][k]=dist[i][k][k-1]+dist[k][j][k-1]; 30 } 31 } 32 int main() 33 { 34 int k,u,v; 35 init(); 36 floyd_dp(); 37 while(cin>>u>>v,u||v) 38 { 39 for(k=0;k<=n;k++) 40 { 41 if(dist[u][v][k]==INF) cout<<"+∞"<<endl; 42 else cout<<dist[u][v][k]<<endl; 43 } 44 } 45 return 0; 46 }
Floyd-Warshall算法不仅能求出任意2点间的最短路径,还可以保存最短路径上经过的节点。下面用精简版的Floyd算法实现这一过程,程序中的图依然对应上面的有向图。
1 #include <iostream> 2 using namespace std; 3 4 const int INF = 100000; 5 int n=10,path[11][11],dist[11][11],map[11][11]; 6 void init(){ 7 int i,j; 8 for(i=1;i<=n;i++) 9 for(j=1;j<=n;j++) 10 map[i][j]=(i==j)?0:INF; 11 map[1][2]=2,map[1][4]=20,map[2][5]=1; 12 map[3][1]=3,map[4][3]=8,map[4][6]=6; 13 map[4][7]=4,map[5][3]=7,map[5][8]=3; 14 map[6][3]=1,map[7][8]=1,map[8][6]=2; 15 map[8][10]=2,map[9][7]=2,map[10][9]=1; 16 } 17 void floyd(){ 18 int i,j,k; 19 for(i=1;i<=n;i++) 20 for(j=1;j<=n;j++) 21 dist[i][j]=map[i][j],path[i][j]=0; 22 for(k=1;k<=n;k++) 23 for(i=1;i<=n;i++) 24 for(j=1;j<=n;j++) 25 if(dist[i][k]+dist[k][j]<dist[i][j]) 26 dist[i][j]=dist[i][k]+dist[k][j],path[i][j]=k; 27 } 28 void output(int i,int j){ 29 if(i==j) return; 30 if(path[i][j]==0) cout<<j<<' '; 31 else{ 32 output(i,path[i][j]); 33 output(path[i][j],j); 34 } 35 } 36 int main(){ 37 int u,v; 38 init(); 39 floyd(); 40 while(cin>>u>>v,u||v){ 41 if(dist[u][v]==INF) cout<<"No path"<<endl; 42 else{ 43 cout<<u<<' '; 44 output(u,v); 45 cout<<endl; 46 } 47 } 48 return 0; 49 }
输入 1 3
输出 1 2 5 8 6 3



