[*]Quadratic Residual Networks: A New Class of Neural Networks for Solving Forward and Inverse Problems in Physics Involving PDEs

 

 

 

 Accepted by SIAM International Conference on Data Mining (SDM21)

本文提出了二次残差网络，通过在应用激活函数之前，添加二次残差项到输入的加权和中，从而获得了比普通DNN具有更好表达容量的模型（相同宽度下）。这样在拟合复杂的PDE时，得益于更少的参数，可以在更少的训练步骤时同样获得很好的精度。最后作者使用了代数几何的工具，从理论上证明了QRes在网络宽度和深度方面表现出更好的参数效应，由于每个神经元中更高的非线性。一般来说，提高神经网络的容量将会有助于学习更复杂的样本，但为了学习更一般的模型，我们也需要通过正则化来平衡网络能力与数据所含的信息，尤其是在训练次数小的时候。

来自物理的额外监督确保PINN使用高容量的神经网络而不会过拟合。如下图所示，物理信息的添加使得神经网络避免了过拟合。

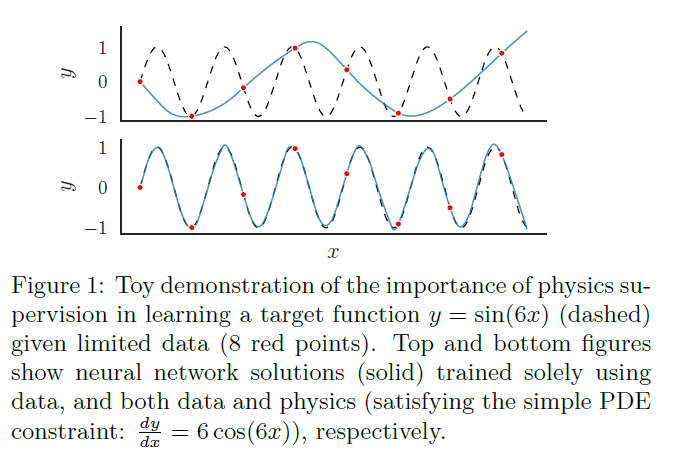
作者关心的是：能否开发一种在每一层都具有更高容量的神经网络架构，该架构可以用比普通DNN更少的参数近似复杂函数。虽然我们知道神经网络的表示能力不会是PINN失败的关键，但是如果可以使用更少的参数近似的话，也可以减少PINN训练的时间。也就是本文的作用大概就是加速PINN的训练。

所提出的网络结构图与普通网络的比较如下。

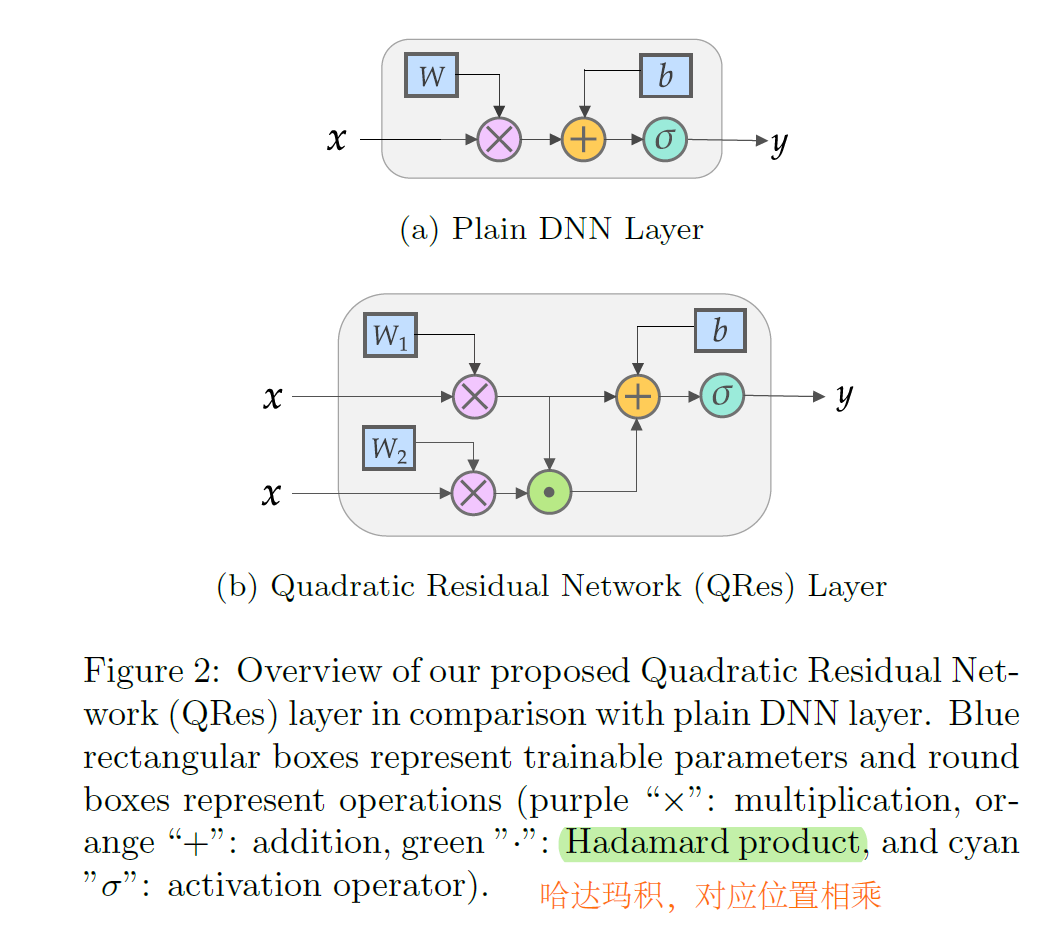
哈达玛积如下：

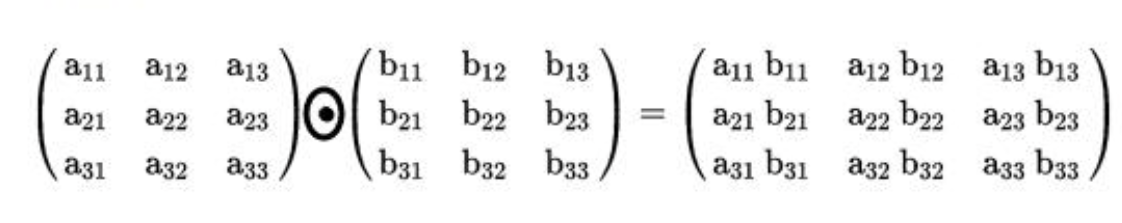
在普通的DNN层只有权重和偏置对输入的影响是线性的，只有激活函数对输入施加线性影响。因此就需要大量合适宽度的DNN层去捕获目标的非线性。称为残差是因为删除了它只会产生一个普通的DNN。W2为0时就是普通网络但当我们需要更好的非线性表达时，QRes就可以获得更高的非线性。网络的数学表示为：

 

虽然作者提出的模型使用线性激活函数，但是为了避免出现无界的情况，作者仍然使用非线性激活函数。借助代数几何分析，所提出的模型具有更高的表示量，但是只有当网络的宽度适合大时才会收敛。

通过下图我们可以看到，QRes可以带来较大的改进。但是需要的神经元较多。

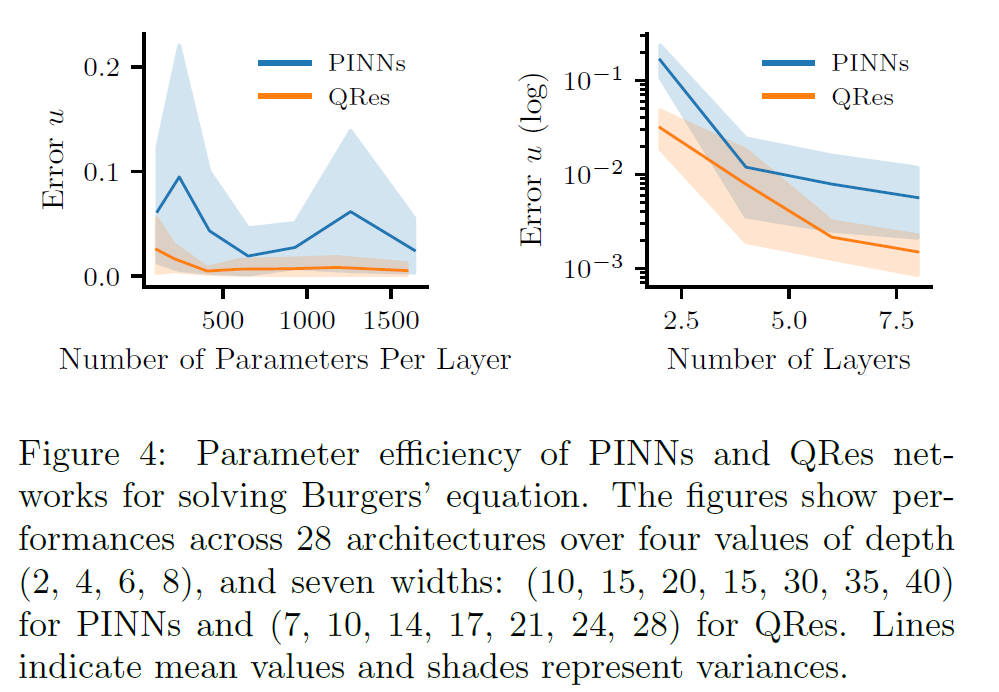
所提出的网络会带来更快的收敛。但是PINN失败的模型，这个也会失败。

 

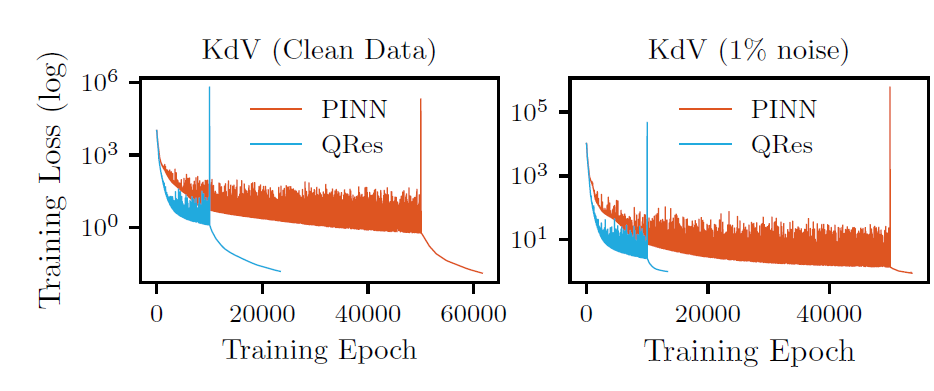
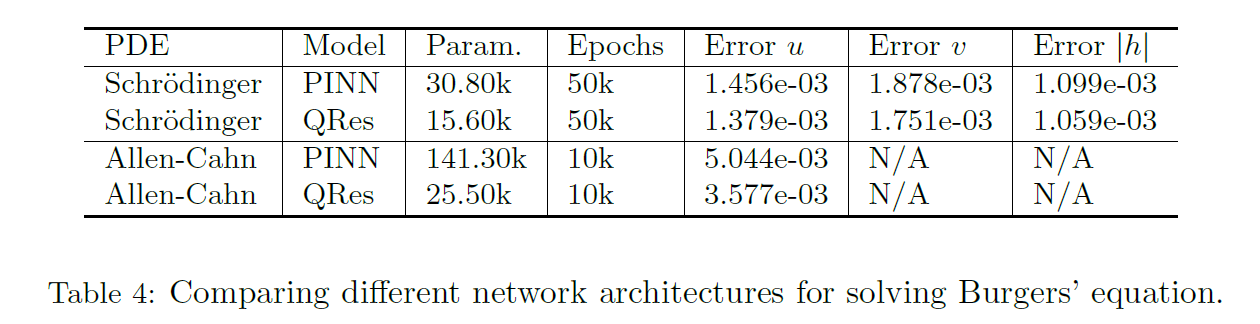
但是性能几乎没有提升，只是单纯收敛的快了。