[*]Kolmogorov n–width and Lagrangian physics-informed neural networks: A causality-conforming manifold for convection-dominated PDEs

本文提供了一种方法来描述PINN训练的困难程度，即将PINN训练的复杂性与解的Kolmogorov n宽度结合起来。同时，作者提出了LPINN用来解决线性和非线性对流扩散方程（在传统的PINN结构中，添加了一个浅分支，最小化由特征残差方程和特征状态变量组成的复合损失）

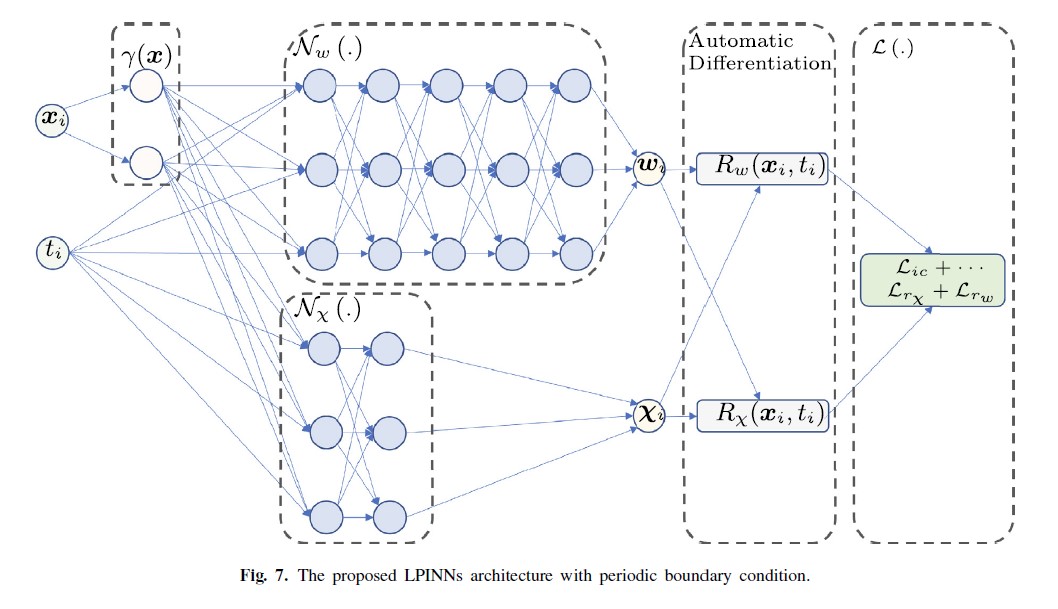
传统的PINN结构如下

目前，PINN在使用过程中存在训练困难的问题，面对许多含有激变的方程，PINN难以找到一个好的解决方案。但是这并不是NN表示能力的欠缺，实验证明神经网络足够表示绝大多数目标方程。关于优化PINN训练的工作有很多第一类如改进ANN的架构和损失来改进训练行为，另一类则使用了系统的先验知识或者性质。如使用了课程学习，序列到序列的学习等等。但本文提到，一些工作[8]在改进的过程中，为了提高解的准确性，违反了解和控制方程之间的一致性。本文将原方程用特征线格式替换，然后使用PINN求解。

本文的作者提出，可以通过奇异值的衰减来反映出PINN训练的难易程度。

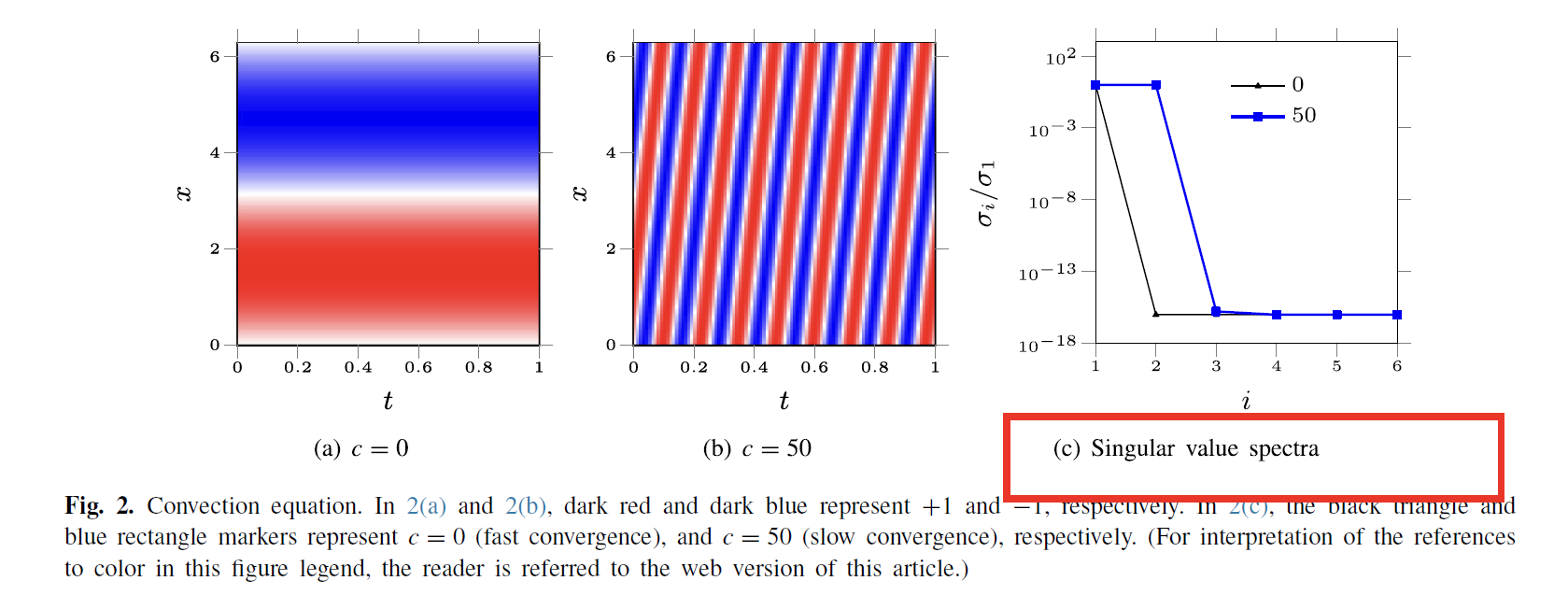
方程如下（c,p越大越难训练）

 

 

 如上所示，PINN会更难训练更高的对流速度。通过多个例子，作者推测出奇异值的衰减与PINN的训练难度相关，当衰减越快时，训练越容易，当衰减越慢时，训练越困难。

通过这个观点，作者认为，优化PINN的一个方向是在流形上重新表述问题，使得

Kolmogorov n宽度减小，或者等效增加奇异值的衰减率。

 

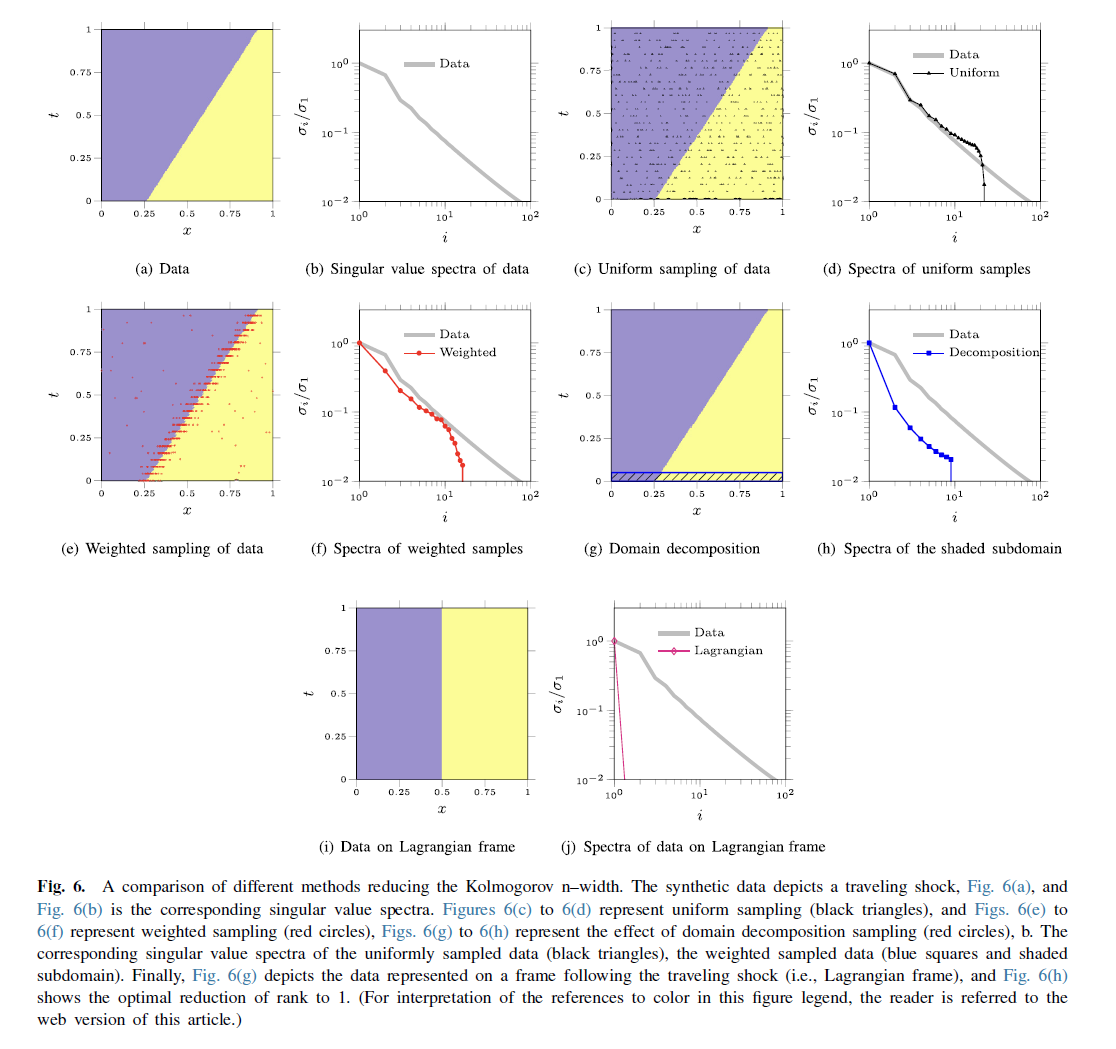
作者给出的几个示例可以看出，像加权采样（利用了梯度信息）和时空域分解（会很繁琐），都使得其意志的衰减率增加，从而在相同的奇异矢量下减少了近似误差。要提到的是，作者在通用近似定理的角度解释了PINN训练。

在近似理论中，Kolmogorov n宽度是n维子空间可以逼近解流行的接近程度的度量。

 

 

 

 

 

 

 

[8]: Limitations of physics informed machine learning for nonlinear two-phase transport in porous media, J. Mach