动态规划--乘积最大子数组

题目：

 

其为动态规划，与上一题的线性求和的方法十分的类似，主要是用dp数组去保存当前最大值，最大值可以为前一个dp[i-1]去运算得到，或者自己重新开始，所以要进行比较，但因为这是乘法，要考虑到正负数的问题

负数越小，那么该数字的绝对值是越大的，所以，如果本身是负数的话，就要求找到其最小值与之相乘，如果是正数的话，那么我们要找到最大值去与之相乘

于是我们可以开辟两个数组，保存最大与最小，还有这个数自己去作比较

 

 

 

 

 

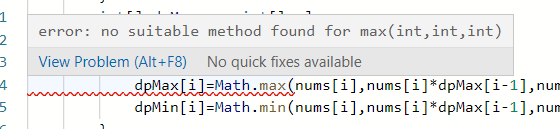
插一句，Math.max函数没有int,int,int,参数，所以要用两个math函数

代码如下

 

 

 

 

 

 

 

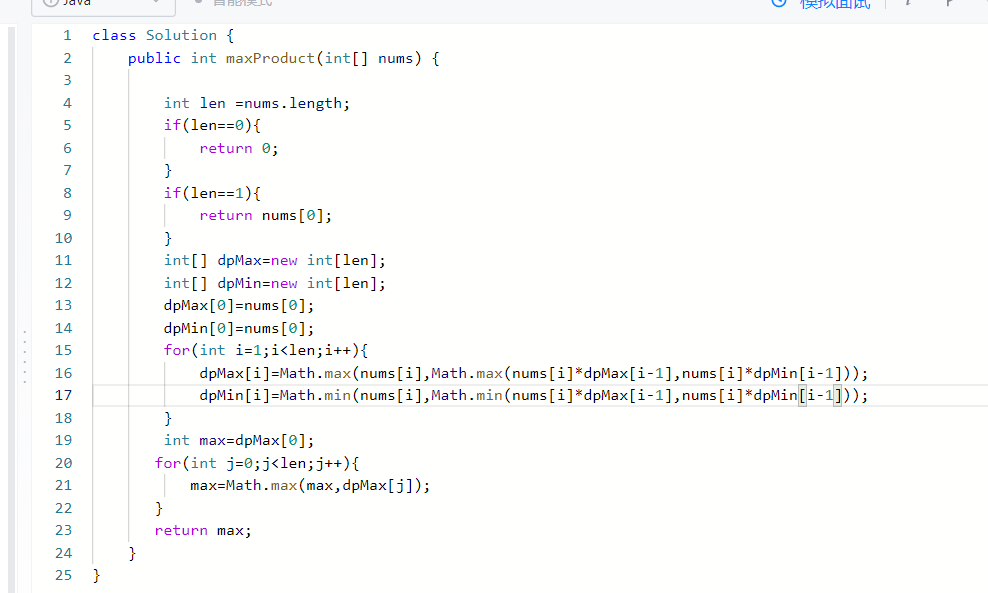
class Solution {
    public int maxProduct(int[] nums) {
       //优化了下性能，
        int len =nums.length;
        if(len==0){
            return 0;
        }
        if(len==1){
            return 1;
        }
        int[] dpMax=new int[len];
　        int[] dpMin=new int[len];

　　　　　　　　dpMax[0]=nums[0];

        　　　dpMin[0]=nums[0];

//动态规划中有dp[i-1]这种类型的数组，于是要判断下i的起始位置，从1开始,既然从1开始，那么就一定要记得对dpMax和dpmin初始化

for(int i=1;i<len;i++){
            dpMax[i]=Math.max(nums[i],Math.max(nums[i]*dpMax[i-1],nums[i]*dpMin[i-1]));
            dpMin[i]=Math.min(nums[i],Math.min(nums[i]*dpMax[i-1],nums[i]*dpMin[i-1]));
        }
//一开始我是赋值为0，后来想想不对，这里面有负数，所以初始化的时候也要适当的思考下
        int max=dpMax[0];
       for(int j=0;j<len;j++){
           max=Math.max(dpMax[j],max);
       }
       return max;
    }
}

 

 AC了，这题和上一题差不多，我感觉我进度没推进，害