【HDOJ2019网络赛】 1002 Rikka with Cake
题目:http://acm.hdu.edu.cn/showproblem.php?pid=6681
大意:对一个 n*m 矩形切 k 刀,每一刀的刀尖从(x, y)开始直到划到边界,保证每一次的操作的x和y都不同,矩形左下角(0, 0),右上角(n, m),输出最终矩形被分为几个部分
L、R、U、D代表刀向左、右、上、下划开
如下图分别是
1 1 U
2 2 L
3 3 L
和
的操作结果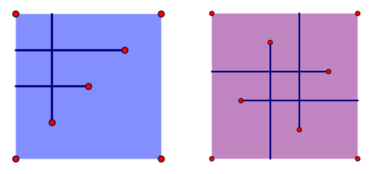
矩形分别被分为3个部分和5个部分
一个重要结论是矩形的部分数目 = 交点数目 + 1
证明:一个交点代表了一个直角的形成,直角的两条边向边界延展,如果中途没有和另一个直角的两条边恰好形成新矩形,那么这两条边就都会和边界相交,与边界形成新的矩形。由于每一次操作的 x 和 y 都不同,因此除去所有新矩形,一定还有一个剩余的部分。所以分块的数目 = 交点数目 + 1
因此用线段树处理出交点数,线段树按 x 坐标建立,维护经过每个点的横向操作数目。
由于矩形大( 边长 1e9 ),先对每个操作的点做离散化,按 x 坐标大小进行编号。
第一次建立线段树,按 y 坐标从大到小处理 k次操作,保证纵向线段在查询时得到的一定是能切割到的横向线段数目。如果操作是 ‘L ’或者 ‘R’ 方向则将该次操作覆盖的区间都 +1 ,如果操作是 ‘U’ 则对操作的点进行查询
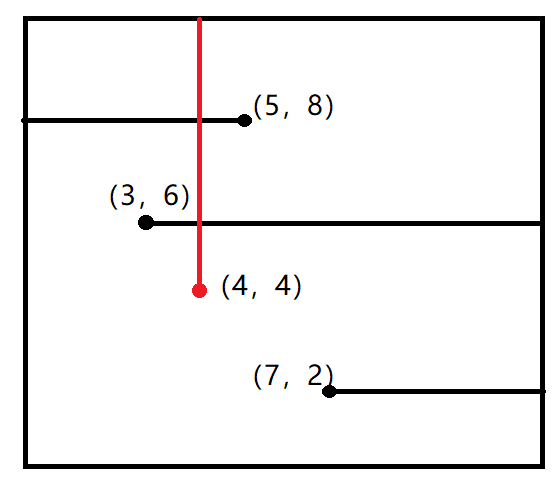
例如上图。
第一次操作:5 8 L 此时 x=1 到 x=5 维护的横线数目是 1
第二次操作:3 6 R 此时 x=1 到 x=2 维护的横线数目是 1,x=3 到 x=5 维护的横线数目是 2,x=6 到 x=13 维护的横线数目是 1
第三次操作:4 4 U 此时对 x=4 查询,得到该操作的交点数 = 2
.......
第二次建立线段树,按 y 坐标从小到大处理 k 次操作,如果操作是 ‘L ’或者 ‘R’ 方向则将该次操作覆盖的区间都 +1 ,如果操作是 ‘D’ 则对操作的点进行查询

#include<bits/stdc++.h> using namespace std; int T; int n,m,k; struct instruction{ int p; int x,y; char d; }a[100005]; struct node{ int l,r,c; int lazy; }tree[100005*4]; int ans; bool cmp(instruction in1, instruction in2) { return in1.x<in2.x; } bool cmp1(instruction in1, instruction in2) { return in1.y>in2.y; } bool cmp2(instruction in1,instruction in2) { return in1.y<in2.y; } void build(int now,int l,int r) { tree[now].l=l; tree[now].r=r; tree[now].c=tree[now].lazy=0; if(l==r) return ; build(now*2,l,(l+r)/2); build(now*2+1,(l+r)/2+1,r); return ; } void update(int now) { int w,len; len=tree[now*2].r-tree[now*2].l+1; w=tree[now].lazy; tree[now*2].lazy+=w; tree[now*2].c+=w*len; len=tree[now*2+1].r-tree[now*2+1].l+1; tree[now*2+1].lazy+=w; tree[now*2+1].c+=w*len; tree[now].lazy=0; return ; } //区间修改 void addin(int now,int l,int r) { if(tree[now].l>=l&&tree[now].r<=r) { tree[now].c+=(tree[now].r-tree[now].l+1); tree[now].lazy++; return ; } int mid=(tree[now].l+tree[now].r)/2; //传递标记 if(tree[now].lazy) update(now); if(l<=mid) addin(now*2,l,r); if(r>mid) addin(now*2+1,l,r); return ; } //单点查询 void qurry(int now,int x) { if(tree[now].l==tree[now].r) { ans+=tree[now].c;return ; } //传递标记 if(tree[now].lazy) update(now); int mid=(tree[now].l+tree[now].r)/2; if(x<=mid) qurry(now*2,x); if(x>mid) qurry(now*2+1,x); return ; } void work() { scanf("%d%d%d",&n,&m,&k); for(int i=1;i<=k;i++) { char s[2]; scanf("%d%d",&a[i].x,&a[i].y); scanf("%s",s); a[i].d=s[0]; } //离散化,按x从小到大编号 ,矩形大小离散为 k*k sort(a+1,a+k+1,cmp); for(int i=1;i<=k;i++) a[i].p=i; //处理切割方向向上的查询 sort(a+1,a+k+1,cmp1); build(1,1,k); for(int i=1;i<=k;i++) { if(a[i].d=='L') addin(1,1,a[i].p); if(a[i].d=='R') addin(1,a[i].p,k); if(a[i].d=='U') qurry(1,a[i].p); } //处理切割方向向下的查询 sort(a+1,a+k+1,cmp2); //重新建树,清空树里的值 build(1,1,k); for(int i=1;i<=k;i++) { if(a[i].d=='L') addin(1,1,a[i].p); if(a[i].d=='R') addin(1,a[i].p,k); if(a[i].d=='D') qurry(1,a[i].p); } printf("%d\n",ans+1); } int main() { scanf("%d",&T); for(int i=1;i<=T;i++) { work(); ans=0; } return 0; }

队友的树状数组只写了 75 行 (。•́︿•̀。)






