【HDOJ】1002 Blow up the city

关于 支配树 的学习

 

题目：http://acm.hdu.edu.cn/showproblem.php?pid=6604

 

大意是在一张DAG图里求所有入度为0的点的支配点数目

 

支配树

给定一个有向图，给定起点S，终点T，要求在所有从S到T的路径中，必须经过的点有哪些(即各条路径上点集的交集），称为支配点。

简而言之，如果删去某个点（即支配点），则不存在一条路径能够使S到达T。由支配点构成的树叫做支配树

 

支配树是一颗由起点S为根的树，根到树上任意一点路径经过的点都是它的支配点。
对于每颗子树，都符合上述性质（即子树内一点到该子树的根路径经过的点都是该子树的根的支配点）

例如对于下图

 

 

 

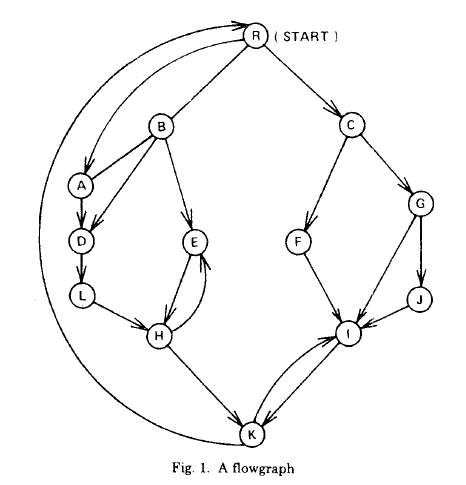
 这是它的支配树，也称流程图

 

 

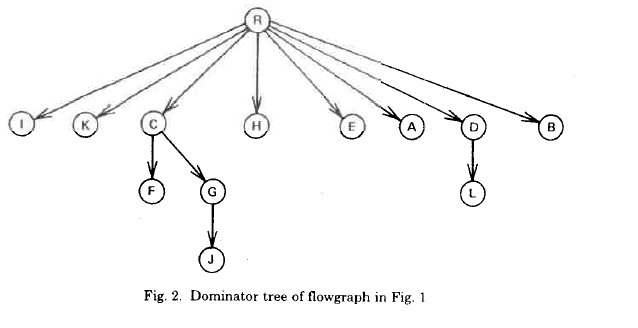
半支配点作为「与支配点有关的线索」存在，点 x 的半支配点 sdom[x] 满足两点定义。

1. 必然存在一条路径从 sdom[x] 到 x ，路径由k个点和 sdom[x] 以及 x 构成。k个点都满足dfs序号大于x（k可以等于0）。

2. sdom[x] 为所有满足第1个条件的点中dfs序最小的。

即 sdom(w)=min{v|有路径v=v0, v1, ..., vk=w使得vi>w对1<=i<=k-1成立}.    

如上图中，对于点 I ，存在路径：R-B-D-L-H-K-I 满足第1个条件

且所有可行的起点序号最小的是R。因此 I 的半支配点的 R 。

原始图的dfs图和半支配点为下：

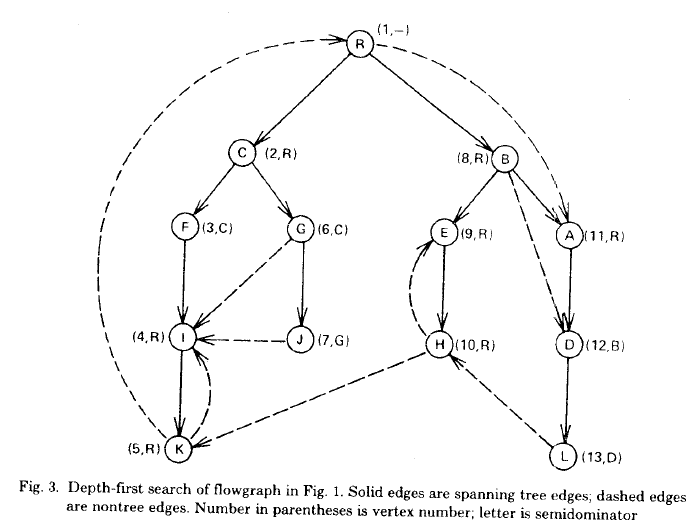
括号内数字是dfs序，字母是该点的半支配点。

在半支配点的定义这里想了好一会_(:з」∠)_