【HDOJ2019网络赛】1005 Path

题目：http://acm.hdu.edu.cn/showproblem.php?pid=6582

大意是删去一些边使最短路变长，求删去的边的最小权值和。

边和点的范围是1e4。

 

如果已经使最短路变长，则之前的最短路都不再连通。如果将符合原来最短路长度的路径全部取出，删去的边的最小代价等价于将这些边分割为多个连通块的最小代价。

因此解法为找出原图的所有建设最短路的边并重新建图，新图的最小割即为所求。

 

网络流：

参考blog：https://blog.csdn.net/zhouzi2018/article/details/81865934

                  https://blog.csdn.net/qq_41357771/article/details/79416899

用水从源点经由流水管道流向汇点，每条管道有相应的容量，询问最后汇点最多能汇聚多少水。

用最暴力的思想，找出每一条可以从源点流到汇点的增广路，枚举每一种水流分流情况，从可行的方案里选择流量最大的。

在这个过程中，枚举的情况其实是相互调整的，直到调整到符合题意为止。在上一种情况选择的边可能会在下一种情况被抛弃。

如果给流经路径‘反悔’的机会，那么我们就可以省下冗余的试探，使得增广路成为一种动态修改的过程。

要抵消从A到B的边，只需要加入权值相同、方向相反的边就可以了。

因此在bfs找可行路径时，边增广边建反边。

这里正反边的编号互为与1的异或值。0和1是一组、2和3是一组。

EK

找到一条从S到T的路径，将其中容量最小的边的权值加入流量，该路径每条正向边都减去流量，反向边加上流量。重复这个过程直到S到T无增广路。

 

Dinic

EK在某些时候可能会浪费时间，比如下图：

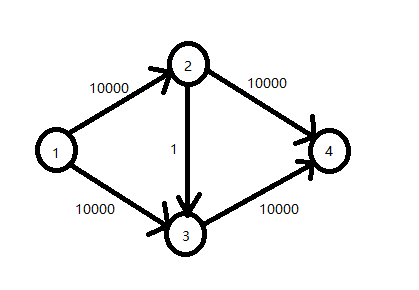
用EK求解，可能会选择1-2-3-4这条路径

 

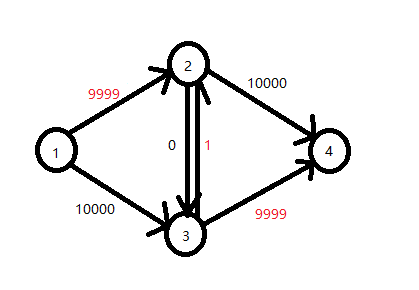
 然后再选择1-3-2-4

 

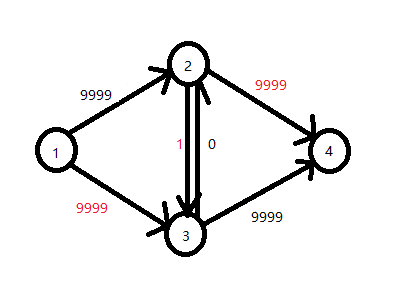
 如果值更大，EK就会超时。

 反复横跳的原因是因为EK在路径选择上没有优先和限制，因此先选择哪条路径做增广是随机的，同时由于反边的建立，图已经不是单纯的有向图，只要策略错误就会对效率有很大影响。

那么能否把图剥离成单纯的有向图？

给每个点一个深度，规定水只能从浅往深流，这样就得到了一个没有小环（仅有两点构成的环）的图。

但这样是否违背了可以‘反悔’的初衷呢？

每做完一次新图的增广，就重新分配一次深度。将图分为多层，上一层选择了水流从A到B的管道，那么下一层就提供水流可以从B到A的管道。由于每一层都要找完该层所有增广路再进入下一层，所以即使做出了耗时的策略，也只会在这一层做出一次，在其他路径被选择前，这个耗时的策略不会再被选择。同时满足了‘回流’和优化。

 

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100001;
int s,t;
int n,m;
struct node{
    int v;
    int next;
}edge[N];
int head[N];
int cnt;
int w[N*2];//正边和反边的权值 
int d[N];//点的深度，每一层清 0 
int q[N],qhead,qtail;
int floor;//这一层的最大流 
int ans;//原图的最大流 
void add(int u,int v,int value)
{
    edge[cnt].v=v;
    edge[cnt].next=head[u];
    w[cnt]=value;
    head[u]=cnt;
    cnt++; 
}
/* 分配深度 */ 
int bfs()
{
    for(int i=1;i<=n;i++) d[i]=0;
    qhead=qtail=0;
    d[s]=1;
    q[++qtail]=s;
    while(qhead<qtail)
    {
        int u=q[++qhead];
        for(int i=head[u];i>=0;i=edge[i].next)
        { 
            if(w[i]>0&&d[edge[i].v]==0)
            {
                d[edge[i].v]=d[u]+1;
                q[++qtail]=edge[i].v;
            }
        }
    }
    /* 如果t未被更新深度，说明从s到t已无增广路 */ 
    if(d[t]>0) return 1;
    else return 0;
}
/* 寻找增广路 */
/* u是当前所在的点，now是当前路径的流量 */ 
int dfs(int u,int now)
{   
    if(u==t) return now;
    for(int i=head[u];i>=0;i=edge[i].next)
    {
        if(w[i]>0&&d[edge[i].v]==d[u]+1)
        {
            /* 继续沿深度往下增广 */ 
            int x=dfs(edge[i].v,min(now,w[i]));
            if(x)
            {
                /* 找到可行增广路，正边减流，反边增加 */ 
                w[i]-=x;
                w[i^1]+=x;
                return x;
            }
        }
    }
    return 0;
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) head[i]=-1;
    for(int i=1;i<=m;i++)
    {
        int u,v,value;
        scanf("%d%d%d",&u,&v,&value);
        /* 建正边和反边，反边剩余容量为0 */ 
        add(u,v,value);
        add(v,u,0);
    }
    s=1;t=n;
    while(bfs())
    {
        /* 遍历当前层的图的所有增广路 */ 
        while(floor=dfs(s,0x7f7f7f))
        {
            ans+=floor;
            floor=0;
        }
    }
    printf("%d",ans);
 } 

 

原题：

#include<bits/stdc++.h>
using namespace std;
const int N = 10001;
int T;
int n,m;
struct node{
    int u,v,next,w;
}e[N*2],E[N];
int head[N];
int HEAD[N];
int w[N*2];
int cnt,CNT;
int s,t;
struct NODE{
    int id,dis;
    friend bool operator < (NODE n1,NODE n2)
    {
        return n1.dis<n2.dis;
    }
};
int vis[N];
int dis[N];
long long f;
int d[N];
long long ans;
bool cmp(node e1,node e2)
{
    return e1.w<e2.w;
}
void add(int u,int v,int c)
{
    w[cnt]=c;
    e[cnt].v=v;
    e[cnt].next=head[u];
    head[u]=cnt;
    cnt++;
}
void ADD(int u,int v,int c)
{
    E[CNT].u=u;
    E[CNT].v=v;
    E[CNT].next=HEAD[u]; 
    E[CNT].w=c;
    HEAD[u]=CNT;
    CNT++; 
}
void read()
{
    scanf("%d%d",&n,&m);
    s=1;t=n;ans=0;
    for(int i=1;i<=n;i++)
    {
        head[i]=HEAD[i]=dis[i]=-1;
        vis[i]=0;
        d[i]=0;
    }
    for(int i=1;i<=m;i++)
    {
        int x,y,c;
        scanf("%d%d%d",&x,&y,&c);
        ADD(x,y,c);
    }
}
void dij()
{
    priority_queue<NODE> Q;
    NODE S;
    S.dis=0;
    S.id=s;
    Q.push(S);
    vis[s]=1;
    dis[s]=0;
    while(!Q.empty())
    {
        NODE U=Q.top();
        Q.pop();
        int u=U.id;
        for(int i=HEAD[u];i!=-1;i=E[i].next)
        {
            if(dis[E[i].v]==-1||dis[E[i].v]>dis[u]+E[i].w)
            {
                dis[E[i].v]=dis[u]+E[i].w;
                if(!vis[E[i].v])
                {
                    vis[E[i].v]=1;
                    NODE V;
                    V.id=E[i].v;
                    V.dis=dis[E[i].v];
                    Q.push(V);
                }
            }
        }
    }
}
void build()
{
    for(int i=0;i<m;i++)
    {
        if(dis[E[i].v]==dis[E[i].u]+E[i].w)
        {
            add(E[i].v,E[i].u,0);
            add(E[i].u,E[i].v,E[i].w);
         } 
    }
}
int bfs()
{
    for(int i=1;i<=n;i++) d[i]=0;
    d[s]=1;
    queue<int> q;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head[u];i!=-1;i=e[i].next)
        {
            if(w[i]&&d[e[i].v]==0)
            {
                d[e[i].v]=d[u]+1;
                q.push(e[i].v);
            }
        }
    }
    return d[t];
}
long long dfs(int u,int now)
{
    if(u==t) return now;
    for(int i=head[u];i!=-1;i=e[i].next)
    {
        if(w[i]&&d[e[i].v]==d[u]+1)
        {
            int y=now;
            if(y==-1||y>w[i]) y=w[i];
            int x=dfs(e[i].v,y);
            if(x)
            {
                w[i]-=x;
                w[i^1]+=x;
                return x;
            }
        }
    }
    return 0;
}
void dinic()
{
    while(bfs())
    {
        while(f=dfs(s,-1))
        {
            ans+=f;
            f=0;
        }
    }
}
int main()
{
    scanf("%d",&T);
    for(int i=1;i<=T;i++)
    {
        read();
        dij();
        build();
        dinic();
        printf("%lld",ans);
    }
}